11. Сандық қатар және оның жинақтылығы. Қатар жинақтылығының қажеттілік белгісі.Анықтамалар (сандық қатар, дербес қосынды, жинақтылық)

Қажеттілік белгісін дәледеу. Гармоникалық қатар

Айталық сан тізбегі берілсін. Егер тізбектін мүшелерін «+» белгісімен тіркестіріп жазсақ, онда

(1,1)

түріндегі сан қатары деп аталатын өрнекті аламыз. Оны қысқаша былай белгілейді:

сандарын қатардың мүшелері деп, ал кез келген нөмірлі мүшесін қатардың жалпы мүшесі немесе –мүшесі деп атайды. Қатар мүшесінің белгілі нөмері бойынша, бұл мүшені жазу ережесі белгілі болса, онда қатарды берілген дейді.

Қатардың алғашқы мүшелерінің қосындысын қатардың -дербес қосындысы дейді. Оны былай белгілейді:

Ал, қатардың мүшелерінің саны шексіз болғандықтан, оның дербес қосындылары деребес қосындылардың шексіз тізбегін құрайды:

Қатар қосылғыштардың шексіз жиындарынан құрылатын болғандықтан, оларды тізбектей біртіндеп қосу арқылы қатар қосындысын анықтау мүмкін емес. Сондықтан, қатар қосындысының анықтамасын келтірейік. Егер дербес қосындысындағы қосылғыштар санын арттырсақ, онда мынандай үш жағдайдың біріне тірелеміз:

1. Дербес қосынды -нің қосылғыштары санын шектеусіз арттырғанда, ол белгілі бір шекке ұмтылады, яғни болады. Бұл жағдайда, қатарды жиынақты деп, ал санын оның қосындысы деп атайды. Сонымен

2. Дербес қосындыдағы қосылғыштар саны шектеусіз артқанда

немесе болады. Бұл жағдайда,

қатарды жинақсыз /шашыранды/ дейді. Шашыранды қатардың қосындысы болмайды.

3. Дербес қосындыдағы қосылғыштар саны шектеусіз артқанда, дербес қосынды ешқандай шекке ұмтылмайды. Бұл жағдайдан да қатарды жинақсыз болады дейді және қатардың қосындысы болмайды. Сонымен, тек жинақты қатардың ғана қосындысы болады екен:

2. Жинақты қатарлардың қасиеттері.

Сандық қатарлардың кейбір қарапайым қасиеттерін қарастырайық.

1-теорема. Егер (1,1)

қатары жинақты және қосынды болса, онда

(1,3)

(с-берілген сан) қатары да жинақты және оның қосындысы 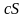болады.

2-теорема. Егер (1,1)

және (1,4) қатарлары жинақты және олардың қосындылары сәйкес және болса, онда

(1,5)

қатары да жинақты және оның қосындысы + болады.

3-теорема. Егер қатар жинақты болса, онда оның кез келген қалдығы да жинақты болады. Егер қатардың қандай бір қалдығы жинақты болса, ол қатар да жинақты болады.

3. Жинақты болудың қажетті шарты.

Қатараларды қарстыруда мынандай екі мәселе туады:

1) қатардың жинақты, не жинақсыз болатынын анықтау, және

2)қатар жинақты болған жағдайда, оның қосындысын табу. Алғашқы есептің теориялық маңызы бар болғандықтан, оны шешу мәселесін қарастырайық. Қатардың жинақты болуының қажетті шартын келтірейік.

4-теорема. Егер қатары жинақты болса, онда оның жалпы мүшесі нөмірі шектеусіз өскенде нолге ұмтылады, яғни

Дәлелдеу.Айталық қатары жинақты және оның қосындысы болсын. Оның

және

дербес қосындыларын қарастырайық. Бұлардан

Сондықтан,

Өйткені және . Мұнда -да . Сонымен, екен.

Салдар. (Қатардың жинақсыз болуының жеткілікті шарты.)

Егер қатардың жалпы мүшесі нөмірі шектеусіз артқанда нөлге ұмтылмайтын болса, онда қатар жинақсыз болады.

Шынында, егер қатарды жинақты десек, онда алдыңғы теоремаға сәйкес қатардың жалпы мүшесі нолге ұмтылған болар еді. Бірақ, бұл шартқа қайшы. Сондықтан, қатар жинақсыз.

Гармоникалық қатар -   сандық қатары. Гармоникалық қатар әрбір мүшесі (екіншісінен бастап) өзімен көршілес екі мүшенің гармоникалық орта мәні болады. Гармоникалық қатар жинақсыз және оның дербес қосындылары   санындай өседі:

,

мұндағы   және С саны Эйлер тұрақтысы деп аталады.   — қатары жалпыланған гармоникалық қатар деп аталады, бұл қатар α>1 болғанда жинақталады және α≤1 болса жинақталмайды.

18.Қайталанбалы тәуелсіз сынақтар. Бернули формуласы. Тәуелсіз п рет тәжірибе жасадық дейік. Әр жолы ізделінді А оқиғаның пайда болу ықтималдығы тұрақты болсын. Онда А оқиғасының пайда болмауы болады. Енді осы тәжірибелер нәтижесінде А оқиғасы k рет пайда болу ықтималдығын деп белгілейді және ол мынаған тең:

Осы формуланы Бернулли формуласы деп атайды.

Егер тәжірибелер саны көп болып (п ), ондағы А оқиғасының пайда

болу ықтималдығы ( ) аз болса, ықтималдықты Пуассон формуласымен есептеу қолайлы:

мұндағы, , және деп есептейміз.

Муавр-Лапластың шектік теориясыТеория-1. Айталық 0<p<1 болсын. Онда |k-np|=o((npq шартын қанағаттандыратын барлық к-лар үшін бірқалыпты түрде (төменде және бүдан былай қарай оң тізбектері үшін жазуы болғандығын білдіреді)

, n

Яғни n кезде sup

{k;|k-np|

Мұндағы ((npq

Теореманы дәлелдемес бұрын мынаған назар аударайык: егер

Функциясын және белгілеуін енгізсек, онда теореманы былай тұжырымдауға болады.

1`-теорема. 0<p<1 болсын . онда барлық үшін

Яғни n кезде

{

Мұндағы ψ(n)=0(npq .

Егер ṗ= белгілеуін енгізсек (3)- формуланы басқаша былай жазуға болады:

Мынадай функция енгізейік:

H(x)=xln Онда (9) формуладан лапластың интегралдық теоремасы тәуелсіз n рет тәжірибе жасағанда ізделінді А оқиғаның пайда болу ықтималдығы тұрақты Р(А)=p болсын. Онда А оқиғасының пайда болу саны мен арасында болу ықтималдығы P_n(k₁,k₂) жуық шамамен мынаған тең:

P_n(k_1,k₂)≈Ф(х₂) – Ф(х₁) мұндағы

Ф(х)= және = x₂=

N артқан сайын муавр-лаплас формуласына мәні дәлірек болады және бұл формуланы npq 20 болған кезде қолданған жөн. Есептеуді оңайлату үшін ықтималдылықтар теориясы оқулықтарында Ф(х)= функциясының кестесі беріледі.бұл функция тақ яғни f(-x)= - f(x), және х артқан сайын функция 1-ге ұмтылады. (х>4 болған кезден бастап 1-ге тең функция деп есептеуге болады)