84 Франк-Герц тәжірибелері.

Электрондардың газдар атомдарымен соқтығысудың кідіртуші потенциалының әдісімен зерттей отырып, Д. Франк пен Г.Герц атомдар энергиясының дискреттік мәнін экспериментпен дәлелдеді.

Оларды орнатудың принциптіктік сұлбас 295 суретте көрсетілген. Сынап буларымен толтырылған вакуумдық түтікше катодтан, екі тордан және анодтан тұрады. Катодпен эмиссияланған электрондар катод пен С₁ тор арасына түсірілген потенциялдар айырымымен үдетіледі. С₂ тор мен анод арасында шағын кідіртуші потенциал түсірілген. Аймақ 1-де үдетілген электрондар торлар арасындағы аймақ 2-ге түседі, мұнда сынап буларының атомдарымен соқтығысады. Соқтығысқаннан кейін аймақ 3-те кідіртуші потенциалды жлю үшін жеткілікті энергияға ие электрондар анодқа дейн жетеді.Егер атомдарда шынында стационар күй өмір сіретін болса, онда электрондар сынаптар атомдарымен соқтығыса отырып, энергияны дискретті белгілі бір порциялармен жоғалтуы тиіс.

Тәжірибеден 296 сурет мынадай қорытынды шығаруға болады. Үдемелі потенциалды 4,86В –ға дейін арттыру кезіңде анодтық ақырын өседі, оның мәні максимум 4,86В арқылы өтеді, содан кейін тосын кемиді.және қайта өседі.

Резерфорд ұсынған теңдеулерін тенестіре отырып осыформуладан мынадай қорытынды шығара аламыз : орбиталар радиустары бүтін сандар квадраттарына пропорционал өседі. Сутегі (Z=1) атомы үшін бірінші бор радиусдеп аталатын n=1 кезіндегі электронның бірінші орьитасының радиусы мынаған тең 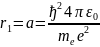. n- дік стационарлық орбитаның радиусыф үшін квантталған мәндіескере отырып, тек қана келесі дискреттік мінге ие болатын электрон энергиясын аламыз

85. Сфералық толқындар теңдеуі- толқын беті былайша жазылады концентистік сфералар түріне ие толқындар деп дәлелдеуге болады, мұндағы r- толқындар центрінен ортаның қарастырылып отырған нүктелеріне дейінгі қашықтық. Сфералық толқындар жағдайында, тіпті энергияны жұтып алмайтын ортада, тербеліс амплитудасы тұрақты болып қалмайды, заңы бойынша қашықтыққа азаятын болады. Фазалық жылдамдық . Егер ортадағы толқындардың фазалық жылдамдығы олардың жиілігіне қатысты болса, онда бұл құбылыс дисперсиялық толқындар, ал толқындардың дисперсиясы байқалатын орта, дисперсияланатын орта д.а. Жалпы жағдайда біртекті изотоптық ортада толқындардың таралуы толқын теңдеуімен дифференциялдық теңдеумен сипатталады

Немесе Кез келгентолқын теңдеуі теңдеудің шешуі болып табылады. X осінің бойымен таралатын жазық толқындар үшін, толқын теңдеуі келесі түрге ие:

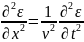
86.Максвелл теңдеулері. Ығысу тогы.

Электромагнит өрісінің теориясын К.Максвелл зерттеп жетілдірді. Бұл теория бойынша:

1)электромагнит өріс екі құраушыдан тұрады:электр және магнит өрістері, олар бір-бірін туғызып ажырамастай байланыста болады.

2)электромагнит өрісі вакуумде жарық жылдамдығымен тарайды;

Максвеллдің төрт теңдеулері ортаның қасиеттерін сипаттайтын материялық теңдеулермен толықтырылады D=

Ығысу тогы. Фарадейдің электромагнит индукция заңынан айнымалы магнит өріс айнымалы электр өрісін туғызады.Максвелл осы сияқты айнымалы электр өрісі магнит өрісін туғызу керек деген болжам жасаған, кейіннен бұл тәжірбие жүзінде дәлелденген. Бір конденсатор алайық, тұрақты көзіне қосайық. Тұрақты ток өту үшін тізбек тұйықталған болу керек, конденсатор арасы диэлектрикпен толтырылғандықтан, тізбекте ток тумайды. Егер корденсаторды айнымалы ток көзіне қоссақ ток пайда болады. Максвеллдің теориясы бойынша кез-кеген айнымалы ток үшін тізбек тұйықталған болып есептеледі және ығысу тогы деген физикалық шамамен сипатталады. Ыгысу тогы айнымалы магнит өрісін туғызады. Сонымен берілген тәжірбиеден айнымалы электр өрісі айнымалы магнит өрісін туғызатынын көреміз. Ығысу тогының шамасын неге байланысты екенін анықтайық. Остроградский-Гаусс теоремасынан электр өрісінің ағыны бұдан уақыт бойынша туында алсақ 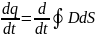және беттік ауданы өзгермесе дербес туынды арқылы жазамыз екенін ескерсек j= –ығысу тогының тығыздығын аламыз. Бұдан уақыт бойынша өзгеретін электр ығысуы кеңістік те ток ығысуын туғызады, екінші жағынан айнымалы ток ығысуы айнымалы магнит өрісін туғызады, Өткізгіш үшін толык ток тығыздығы j_толык=j_от+j_ығы= j_от+ .

Интеграл түріндегі Максвеллдің төрт теңдеуі

физикалық мағынасы:уақыт бойынша өзгеретін магнит индукциясы кеңістікте құйынды электр өрісін туғызады.

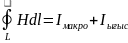немесе Физикалық мағынасы:магнит өрісі өткізгіштік ток пен ығысу тогынан пайда болады немесе уақыт бойынша өзгеретін электр индукциясы құйынды магнит өрісін туғызады.

физикалық мағынасы:заряд электр ығысуының көзі болып табылады, электростатистикалық өрісте электр ығысуы зарядтан басталып, содан аяқталады.

Физикалық мағынасы: магнит индукциясының электр ығысуы сияқты зарядтың көздері болмайды. Магнит индукциясын туғызатын ток зарядтардың қозғалысынан пайда болады.

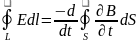1)Сток теоремасынан екінші жағынан олай болса rotE=- .

2) Сток теоремасынан екінші жағынан олай болса rotH= .

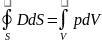3) екінші жағынан олай болса

4) Гаусс теоремасынан бұдан divB=0.

Сонымен rotE=- және divB=0 теңдеулерін Максвелл теңдеулерінің бірінші қосағы, ал rotH= және теңдеулерін екінші қосағы деп атайды.

87 Когерентті толқындар- жиіліктері бірдей және фазалар айырымы уақыт бойынша өзгермейтін толқындар.

Интерференция- жарық толқындарының кеңістікте қабаттасу нәтижесінде бірін бірі күшейтуі немесе әлсіретуі. Интерференция болу үшін толқындар когерентті болуға тиіс. Егер толқындар когерентті болмаса, онда толқындар интенсивтілігінің қосындыларын аламыз, интерференция құбылысы байқалмайды. Жарық толқыны көлденең болғандықтан инт.болуы үшін электр өрісінің векторларының бағыттары бірдей түзудің бойымен тербелуі тиіс. Лазерлер толқынынан басқа жарық көздерінен когерентті толқындар алу үшін, бір қосақ жарық толқынын екіге айыру нәтижесінде аламыз. Суретте көрсетілгендей параллель түскен бір толқыннан S1 және S2 тесіктерден өтетін когерентті толқындар аламыз. Экран бетінде ашық және күңгірт жолақтар, яғни инт.көрінісі байқалады. Толқындар фазалары бірдей болса, толқындар бір бірін күшейтеді. Қарама қарсы болса әлсіретеді. Күшейту немесе әлсірету жол айырмасына байланысты. Кеңістіктегі кез келген нүктедегі қорытқы амплитудасы 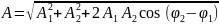бұдан егер фазалар айырмасы болса, онда cos болады да тербеліс амплитудасы максимум мәнге ие болып, бір бірін күшейтеді. Сонымен жолдаар айырмасы жарты толқындардың жұп санына тең болса, онда жарық толқындары бірін бірі күшейтеді. 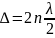Осы тәріздес 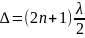жолдар айырмасы жарты толқындардың тақ санына тең болса, онда жарық толқындары бірін бірі әлсіретеді. Көршілес екі жарық жолақтың ара қашықтығы

87. Фотондар- электомагниттік сәуленің кванты. Жарық сәулесінің энергиясының шығарылып (жұтылуы), сонымен қатар кеңістікте таралуы және заттармен әсерлесуі фотондар бөлшегі арқылы сипатталады. Фотонның энергиясы , Массасы. Эйнштейн формуласын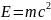ан , бұдан Импульсі . Векторлық түрде бұдан импульстің бағыты электромагнит сәулесінің таралу бағытымен сәйкес келеді, мұндағы K- толқындық сан. Фотонның тыныштық массасы . Олай болса энергия мен импульстің арасындағы қатынас . Тыныштық массасы нөлге тең болғандықтан, тек қозғалыста өмір сүре алады. Сонымен фотон бөлшек сияқты энергиясы, массасы, импульсі болады. Фотонның осы үш корпускулалық сипаттамалары жарықтың жиілігімен байланысты. Фотонның корпускулалық қасиетін тәжірибе жүзінде сыртқы фотоэффект, Комптон эффектісі және жарықтың қысымы дәлелдейді.

88.Толқын- тербелістің кеңістікте таралу процесі. Толқын тарайтын ортаның бөлшектері толқынмен ілесіп кетпейді, олар өзінің тепе- теідік қалпының маңында ғана тербеледі. Толқын таралатын бағытпен салыстырғандағы бөлшектер тербелістің бағытына байланысты қума және көлденең болып екіге бөлінеді.

Көлденең толқын – ортаның бөлшектері толқынның таралу бағытына перпендикуляр тербеледі.

Қума толқын- ортаның бөлшектері толқынның таралу бағыты бойынша тербеледі.

Механикалықкөлденең толқындар ығысу кедергісі бар ортада ғана пайда бола алады. Сондықтан сұйық және газ тектес ортада тек қума толқын тарай алады. Уақыт өтуіне байланысты орта бөлшектерінің қозғалысы берілген, әр түрлі бөлшектер фазасы бойынша тербеледі.

Толқын ұзындығы- бірдей фазада ең жақын орналасқан бөлшектердің арақашықтығы. немесе λ=

Толқын фронты – бір уақыт мезетінде тербеліс келіп жеткен нүктелердің геометриялық орны.

Толқындық бет – бірдій фазада тербелетін нүктелердің геометриялық орны. Қарапайым толқындық бет жазық немесе сфеоралық болады. Жазық толқында толқындық беттер бір біріне параллель жазықтарда , ал сфералық толқында – концентрлік сфералар түрінде болады.

Толқын теңдеуі тербелістегі нүктенің ығысуын x,y,z координаталары мен t уақыттың функциясы ретінде беретін өрнек.

Фазалық жылдамдық –фазаның орын ауыстыру жылдамдығы. Толқын фазасы мәнімен анықталады. Берілген фазада барлық нүктедегі тербеліс амплитудасы бірдей болады, олай болса . Осы өрнекті диференциалдай отырып фазалық жылдамдығы табамыз. dt- -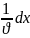 =0.

Толқындық сан - 2 ұзындығына қаншалықты толқын ұзындығы сәйкес келетін сан k= = .

Жазық толқын теңдеуін толқындық сан арқылы өрнектейік ξ=acos( Негізен л векторлық шама толқынның таралу бағытын көрсетеді k=ki. kx=kr, мұндағы r- радиус векторы, олай болса , кез келген бағытта таралатын жазық толқынның теңдеуі ξ=acos( . Изотроптыжәне толқын энергиясын жұтпайтын ортада тарайтын толқын, дербес диференциалдық теңдеуменсипатталады, оны толқындық теңдеу деп атайды. Оның түрі мұндағы Лаплас операторы. Жазық толқынның осы теңдеуі қанағаттандыратын дәлелдеік. acos( , (7)

acos(

acos(

acos( ,

., ξ=- олай болса , ,

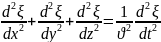
Лаплас операторы арқылы жазсақ дәлелдеу керегі де осы еді. Толқынның энергиясы.

Серпімді ортада тарайтын толқын энергиясы тербеліс жасайтын бөлшектердің кинетикалық энергиясы мен деформация салдарынан туатын потенциялдық энергияның қосындыларынан тұрады. Жазық қума толқын таралатын элементар көлем бөліп алайық Е_к және Е_р энергиялары мұндағы 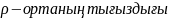, жылдамдығы.

Толқын энергиясы

Энергияның тығыздығы w=

Жазық толқын үшін

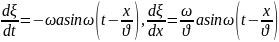
Онда w= орташа мәні . Тараған толқынн көзімен бірге энергия тығыздығы да тасымалданады. Кеңістіктің әр түрлі нүктелеріндегі энергия ағынын сипаттау үшін энергия ағынының тығыздығы деп аталатын векторлық шама еңгізу, оны алғашқы рет Н. Умов енгізгін j= . Мұндағы Ф энергия ағыны Ф=

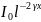Умов векторының абсолюттік шамасы толқынның интенсивтілігін береді. I=│ │, I=│ │= . Амплитудасы A= интенсивтілігі I= . Жұтылатын ортадағы жазық толқынның теңдеуі