81 .Дифракцилық тор. Голография принципі.

Дифракцилық тор-бірдей өзара параллель орналасқан саңылаулар жиынтығы. Мөлдір саңылаудын енін b, ал мөлдір емес а деп белгілесек, дифракциялық тордың периоды d=b+a өрнегімен анықталады. Торға перпендикуляр түскен толқынның дифракциясын қарастырайық.

Суреттен екі шеткі сәулесінің жол айырмасы Δ=dsin . Дифракцияланған монохромат жарықтың max шарты dsin = 𝜆, m=0,1,2…

мin шарты dsin = 1)𝜆

Соныменен дифракциялық торға монохроматты жарық шоғы түскенде жарық шоқтарын бөліп тұратын өте енсіз күңгірт жолақтар, яғни сызықтар пайда болады. Егер ақ жарық түссе, дифракциялық жолақтар толқын ұзындықтарына қарай қызылдан күлгін түске дейін жіктеледі. Орталық ашық жолақтан оң және сол жағында түрлі түсті жолақтар болады. Жарықтың әр түрлі түске жіктелуін дифракциялық спектрлер дейді. Дифракциялық торлар күрделі жарық құрамын зерттеу үшін пайдалынылады, оны спектрометр деп атайды. Спектрометрдің ажыратқыш қабілеті R= =mn, (m=0,1,2…), n-тордағы саңылау сандары. Бұрыштық дисперсиясы Q= , к-спектрдің реттік саны. Тордың периоды d=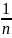 мұндағы n=1 мм ішіндегі штрихтер саны. Оптикалық құралдар үшін объективтің ажыратқыштық қабілеттілігі R= , мұндағы

Егер кристал бетіне толқын ұзындығы монохроматты рентген сәулелері бұрыш жасап түссе, атомдық жазықтығында жатқан атомдардан шағылады. Шашыраған 1 және 2сәулелерінің оптикалық жолдарының айырмасы Δ=2dsin .интенсивтілігі максимум болу үшін мына шарт орындалуға тиіс 2dsin =k𝜆, k-шағылған сәулелердің реттік саны. Осы теңдеуді Вульф-Брегтер формуласы деп аталады. Берілген формула рентген сәулелерінің спектрі жайындағы ілімді және кристалл құрылымын зерртеуге мүмкіндік береді.

Голография-интерференциялық көріністерді толық жазып және оны қалыпына келтіретін ерекше тәсіл. Голография интерференция құбылысына негізделгеннен кейін қабаттасқан толқындар когерентті болуы тиіс, сондықтан лазерлерді қолданады. Фото суреттерде тек заттан шағылған толқындардың амплитудасы тіркеледі, ал кеңістік голографиясында фазада тіркелуі қажет. Сонымен голография негізі мынада:нәрседен шағылған толқындар мен оған когерентті фазасы белгілі жарық көзінен келген толқындардың интерференциясын арнаулы пластинкаға түсіріліп, голограмма алады. Голография әдісі голографиялық электронды микроскопта, голографиялық кино мен теледидар және т.б. жерлерде қолданылады.

83 .Өшетін тербелістер,диф. Теңдеуі. Амплитудасы.Логарифдік декремент.

Еркін өшетін тербелістер – ортаның кедергісі салдарынан, жүйесінің энергиясы кеміп,уақыт бойынша амплитудасы азайып отыратын тербелістер.

Кез-келген нақты тербеліс жүйесінде тербеліс өшеді. Механикалық тербелістерде өшу ортаның кедергісі, ал электр тізбектерінде өткізгіштің жылу шығару салдарынан болады.Еркін өшетін тербелістін теңдеуін қорытып шығарайық.Мысал ретінде серіппеге ілінген жүктің тербелісін алайық.Ортаның кедергі күші мен серіппенің серпімділік күші

, F_сер=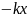 . Мұндағы r – кедергі коэфициенті, «-» таңбасы f_r мен V жылдамдық шамаларының бағыттары қарама-қарсы.Ньютонның екінші заңынан белгілесек

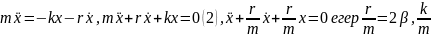
еркін өшетін тербелістің теңдеуін аламыз. Мұндағы өшу коэффициенті деп аталады, жүйенің меншікті жиілігі.Шешімі мұндағы a(t) уақыт бойынша кеміп отыратын амплитудасы, оның мәнін табу үшін туындылары (2) теңдеуге қойып, түрлендіреміз

tуақыт шамасының кез-келген мәнін қанағаттандыру үшін 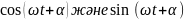коэффициенттері нөлге тең болу керек

(3) теңдеуінен интегралдасақ

. Бұдан тербеліс амплитудасы экспоненциал заңымен өшетінін көреміз. Мұндағы уақыттың бастапқы мезетіндегі амплитудасы. Сонымен өшетін тербелістің шешімі . Бұл функцияның графигі (11-сурет) берілген.

Өшетін тербелістің жиілігі мен периоды. (3) теңдеуге мәндерін қойсақ теңдеуін аламыз, бұдан тербеліс жиілігі

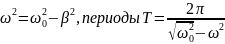
Тербеліс жиілігінің нақты мәні болу үшін болуға тиіс. Бұдан тербеліс болу үшін ортаның кедергісі өте үлкен болмауы тиіс. Өшу коэффициенті өскен сайын тербеліс периоды артады.

Логарифмдік декремент. Тербеліс амплитудасы экспоненциал заңымен кемігендіктен, бір периодқа сәйкес уақыт мезетінде амплитудалар қатынасын өшу декременті деп, оның логарифмі өшудің логарифмдік декременті деп аталады . Амплитудасы е есе кемитін уақытты релаксация уақыт деп атайды 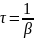. Олай болса мұндағы тербеліс саны, демек логарифмдік декремент тербеліс санына кері шама. Тербелмелі жүйені сипаттау үшін жүйе сапалығы деп аталатын физикалық шаманы енгіземіз . Бұдан сапалық амплитуда е есе кемитін уақыт ішінде жасалатын тербеліс санына пропорционал. Тербеліс периодының формуласынан егер болса, тербеліс периоды шексіздікке немесе нақты мәні болмайды. Қозғалыс тербеліссіз болып оны периодтық қозғалыс деп аталады. Бастапқы шарттанрына байланысты периодтық қозғалыс кезінде тепе-теңдікке келтірудің екі жолы бар (12-сурет). 2-ші қисықта болуға тиіс, қалған шарттарда 1-ші қисық сәйкес келеді.

Еркін өшетін тербеліске мысал ретінде активті кедергісі бар контурдағы тербелісті қарастыруға болады.Бұл жағдайда конденсатордағы заряд тербелісінің дифференциалдық теңдеуі немесе

мұндағы