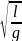- •3. Өздік және өзара индукция құбылыстары. Индуктивтілік.
- •4.Тоқтың магнит энергиясы. Магнит өрiсi энергиясының көлемдiк тығыздығы.
- •5.Электромагниттік өріс үшін Максвелл теориясының жалпылама сипаттамасы. Максвелл теңдеулер жүйесі. Электр және магнит өрістерінің салыстырмалылығы.
- •6. Ығысу тоғы. Ығысу тогынын тығыздығы.
- •7. Электр тiзбегiн тұйықтау және ажырату кезiндегi экстратоктар.
- •8.Тербелмелі процесстер. Гармоникалык тербелiстердiң жалпы сипаттамасы.
- •9.Гармоникалык терб. Диф. Тендеyi. Гармоникалык тербелiс энергиясы.
- •10.Гармоникалық осциллятор. Серіппелі, физикалык, математикалык маятник, тербелмелi контур.
- •11.Бір бағытта тербелетін екі тербелісті қосу. Векторлық диаграмма. Соғу.
- •12.Еркін өшетін тербелістер және оның сипаттамасы. Өшу коэффициенті, өшудің логарифмдік декременті. Сапалылық.
- •13.Еріксіз тербелістер. Дифференциалды тендеулерi және оның шешiмдерi. Ерiксiз тербелiс фазасы және амплитудасы. Резонанстык кисыктар.
- •14.Толқындық қозғалыстың негізгі сипаттамасы. Сфералық және жазық толқын. Толқын теңдеуі. Фазалык жане топтык жылдамдык.
- •15.Серпімді толқындык тендеу.Толкын энергиясы. Энергия ағыны. Умоф векторы.
- •16.Толқындардың суперпозиция принципі. Топтық және фазалық жылдамдық және олардың арасындағы байланыс. Толқын интерференциясы. Калыпты жане аномальды дисперсия.
- •22.Дифракция. Бір саңылаудағы дифракция. Дифракциялық тор.
- •23. Жарык поляризациясы. Еки диэлектрик ортанын шекарасындагы жарыктын шагылуы мен сыну кезиндеги поляризация.
- •24.Жылулық сәуле шығару. Жылулық сәуле шығару заңдары. Абсолют қара дененин сауле шыгару проблемелары. Планк формуласы және гипотезасы. Кирхгоф заны. Рэлей-Джинс формулалары.
- •25.Фотондар. Жарық кванттарының энергиясы және импульсі. Жарык кысымы.
- •26.Комптон эффектісі және оның элементар теориясы.
- •27. Фотоэффект. Фотоэффект заңдары. Фотоэффект үшін Эйнштейн теңдеуі.
- •28.Заттардың толқындық-корпускулалық дуализмі.Де Бройль гпотезасы жане оны экксперименталды растау. Де Бройль толкынынын касиеттері.
- •34.Сутегі атомында электрондардың күй бойынша үлестірімі. Сәуле шығару және жұтылу спектрі.
- •35.Электромагниттік сәуле шығарудың зат пен өзара әсерлесуінің кванттық табиғаты. Спонтанды және еріксіз сәуле шығарулар. Лазер.
- •36.Кванттық статистика элементтері. Ферми-Дерак және Бозе-Эйнштейн кванттық статитикалары туралы түсінік. Бозондар және фермиондар.
- •37. Кристалдардагы энергетикалык аймактар. Катты денелердин аймактык теорисындагы металдар, диэлектриктер, жартылай откизгиштер.
- •38.Металдардын электр откизгиштиги. Ферми денгей.
- •48. Ядроның байланыс энергиясы. Массалық ақау.
- •49. Кванттык сызыктық гармоникалық оссилятор.
- •50 Бір жаққа бағытталған екі тербелістерді қосу. Қорытқы тербелістің теңдеуі
- •52 .Кванттық статистика туралы жалпы мағлұматтар. Боза Эйнштейн бөлінуі. Бозондар.
- •53 , Кванттық теория бойынша сутегі атомы. Энергетикалық деңгейлер. Кеңістіктік кванттау. Электрон спині. Паули принципі.
- •54 Өздік және өзара индукция.Ленц ережесі
- •56 Гармоникалық тербелістер, олардың сипаттамалары.
- •57 Шредингер теңдеуі. Шредингердің стационар теңдеуі
- •58 Механикалық тербелістер. Физикалық маятник тербелісінің периодын қорыту.
- •59 Гейзенбергтің анықсыздықтар ара қатынасы.
- •60 Механикалық тербелістер. Математиткалық маятниктің тербеліс периодын қорыту.
- •61 Жылулық сәуле шығару. Энергетикалық жарқырау , шығару қасиеттері. Абсолют қара дене, оның сәуле шығару заңдары.
- •62Өшетін механикалық тербелістер. Серіппіге ілінген жүктің өшетін тербелісі. Өшу коэффициенті. Өшудің логарифмдік декременті. Беріктілік.
- •63. Фотон . Фотон импульсы энергиясы . Комптон эффектісі.
- •64. Жартылай өткізгіштер. Жө меншікті өткізгіштігі. Фотокедергі.
- •65. Жылулық сәуле шығару. Планк формуласы. Кирхгоф заңы.
- •66. Электромагниттік тербелістер. Тербелмелі контур.Томсон ф-н қорыту
- •67. Жарықтың жұтылуы мен сейілуі.Жарық дисперсиясы. Ньютон спектрі.
- •68 Кристалл ішіндегі электрондардың стационар күйлері.Ферма деңгейі. Азғындалған электрон газы.
- •70 .Кванттық статистика туралы жалпы мағлұматтар. Боза Эйнштейн бөлінуі. Бозондар.
- •71. Кванттық теория бойынша сутегі атомы. Энергетикалық деңгейлер. Кеңістіктік кванттау. Электрон спині. Паули принципі.
- •72.Айнымалы электр тогы. Айнымалы тоқ үшін Ом заңын векторлық диаграмма арқылы қорыту.
- •73.Атом ядросының масса ақауы ж/е байланыс энергиясы.
- •74.Толқындардың суперпозиция принципі. Топтық жылдамдық пен фазалық жылдамдықтар. Дисперсия.
- •75 Өздік және өзара индукция.Ленц ережесі
- •76Тікбұрышты потенциалдық шұңқыр ішіндегі бөлшек.Туннельді эффект
- •77. Өзара перпендикуляр бағытталған тербелістерді қосу.Лиссажу фигура
- •78.Жарық дифракциясы. Гюгейнс-Френель принципі. Френель зоналары, олардың қолданылуы.
- •79.Жартылай өткізгіштердің қоспалы өткізгіштігі.
- •80.Фотоэффект заңдары. Эйнштейннің фотоэффектке арналған теңдуі
- •81 .Дифракцилық тор. Голография принципі.
- •83 .Өшетін тербелістер,диф. Теңдеуі. Амплитудасы.Логарифдік декремент.
- •84 Франк-Герц тәжірибелері.
- •86.Максвелл теңдеулері. Ығысу тогы.
- •88.Жартылай өткізгіштер. Жө жанасу потенциалы. Р-n ауысуы. Оның волтьамперлік сипаттамалары.
- •10. Фотон . Фотон импульсы энергиясы . Комптон эффектісі.
- •11. Жартылай өткізгіштер. Жө меншікті өткізгіштігі. Фотокедергі.
- •12. Жылулық сәуле шығару. Планк формуласы. Кирхгоф заңы.
- •13. Электромагниттік тербелістер. Тербелмелі контур.Томсон ф-н қорыту
- •14. Жарықтың жұтылуы мен сейілуі.Жарық дисперсиясы. Ньютон спектрі.
- •16.Радиоактивтік ыдырау заңы.Жартылай ыдырау периоды. Радиоактивтік ыдырау түрлері.
- •19Еріксіз электр тербелістері.Резонанстықтық қисықтар
- •20 Кристалл ішіндегі электрондардың стационар күйлері.Ферма деңгейі. Азғындалған электрон газы.
- •21 Бір жаққа бағытталған екі тербелістерді қосу. Қорытқы тербелістің теңдеуі
- •23.Кванттық статистика туралы жалпы мағлұматтар. Боза Эйнштейн бөлінуі. Бозондар.
- •24. Кванттық теория бойынша сутегі атомы. Энергетикалық деңгейлер. Кеңістіктік кванттау. Электрон спині. Паули принципі.
- •25.Айнымалы электр тогы. Айнымалы тоқ үшін Ом заңын векторлық диаграмма арқылы қорыту.
- •26.Атом ядросының масса ақауы ж/е байланыс энергиясы.
- •27.Толқындардың суперпозиция принципі. Топтық жылдамдық пен фазалық жылдамдықтар. Дисперсия.
- •28 Өздік және өзара индукция.Ленц ережесі
- •30. Өзара перпендикуляр бағытталған тербелістерді қосу.Лиссажу фигура
- •31.Жарық дифракциясы. Гюгейнс-Френель принципі. Френель зоналары, олардың қолданылуы.
- •32.Жартылай өткізгіштердің қоспалы өткізгіштігі.
- •33.Фотоэффект заңдары. Эйнштейннің фотоэффектке арналған теңдуі
- •48.Өшетін тербелістер,диф. Теңдеуі. Амплитудасы.Логарифдік декремент.
- •39 Франк-Герц тәжірибелері.
- •41.Максвелл теңдеулері. Ығысу тогы.
- •47.Жартылай өткізгіштер. Жө жанасу потенциалы. Р-n ауысуы. Оның волтьамперлік сипаттамалары.
- •12) Энергияның сақталу және айналу заңы.
- •47 Сұрақ Магнит өрiсi.............................
57 Шредингер теңдеуі. Шредингердің стационар теңдеуі
Кванттық
механиканың негізігі теңдеуі болып,
толқындық функцияға арналған Шредингердің
1926ж ашқан ұсақ бөлшектер күйін
сипаттатйтын теңдеуі жатады. Бұл теңдеу
бұрыннан белгілі қатынастардан
қорытылып шығарылмай, тек көптеген
ғылыми тәжірибелердің нәтижелерінен
табылады. Шредингер теңдеуінің жалпы
түрі: - (1)
(1)
Мұндағы
h=h/2п=1,05*10-34
Дж*с, m-бөлшектің массасы, U=(x,y,z,t)-күштер
өрісіндегі бөлшекте потенциалдық
энергиясы, i- жорамал сан, - бөлшектің
кеңістіктегі координаты.
- бөлшектің
кеңістіктегі координаты.
(1)
теңдеудегі Ψ функциясы потенциалдық
өрістегі бөлшекке әсер ететін күштердің
потенциалдық энергиясы арқылы анықталады.
Сөйтіп, U потенциалдық энергия уақыт
пен кордината фунциясы екендігін
байқаймыз, яғни Ψ(х,у,z,t) Е – бөлшектің толық энергиясы. Егер
(2) өрнекке 1 теңдеудегі функция мәндерін
қойып, дифференциалдық теңдеуін аламыз:
Е – бөлшектің толық энергиясы. Егер
(2) өрнекке 1 теңдеудегі функция мәндерін
қойып, дифференциалдық теңдеуін аламыз:
 (3) Осы теңдеу Шредингердің бөлшектің
стационарлық күйін сипаттайтын теңдеу.
(3) Осы теңдеу Шредингердің бөлшектің
стационарлық күйін сипаттайтын теңдеу.
58 Механикалық тербелістер. Физикалық маятник тербелісінің периодын қорыту.
Тербеліс – белгілі бір дәрежеде уақыт бойынша қайталанып отыратын процестер.
Тербелістер:
механикалық, электромагниттік,
электромеханикалық. Гармоникалық
осциллятор – х”+wx=0 теңдеуімен
сипатталатын жүйе. Мысалы: математикалық
және физикалық маятниктер, пружинаға
ілінген жүктің тербелісі, тербелмелі
контур. Физикалық маятник – оның инерция
центріне дәл келмейтін қозғалмайтын
нүкте маңында тербеліс жасайтын қатты
дене. Т= 2П/ w, W= , T=2П
, T=2П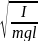 ,
lкел=
,
lкел= ,
T=2П
,
T=2П
59 Гейзенбергтің анықсыздықтар ара қатынасы.
Классикалық физикада траектория бойымен қозғалған дененің кез келген уақытта орны мен импульс мәндері болады. Элементар бөлшектер әлемінде бөлшектердің толқындық қасиеттері болған соң траектория деген түсінік болуы мүмкін емес. Сондықтан физикалық шамалар физикаға қарағанда басқаша қатынаста болады. Мысал ретінде х кординатасы мен Рх физикалық шамалардың қатынастарын қарастырайық. Жазық де Бойль толқыны х осі бойынша тарасын. Бұл жағдайда импульс қандай да болса бір мәнге ие болады. Рх =Pz=0, Py=P.
Енді
саңылау арқылы орнын тауып көрейік.
Саңылаудан өткен кезде электронның
орны шамасында анықтай аламыз, бірақ дифракция
салдарынан импульс алғашқы бағытынан
аутқып, саңылауға дейіңгі нақты мәнін
жоғалтады. Суреттен
шамасында анықтай аламыз, бірақ дифракция
салдарынан импульс алғашқы бағытынан
аутқып, саңылауға дейіңгі нақты мәнін
жоғалтады. Суреттен
 бірінші дифракция максимум шартынан
бірінші дифракция максимум шартынан
 Егер де дифракция суретінің басқа да
максимумдерін ескерсек:
Егер де дифракция суретінің басқа да
максимумдерін ескерсек:
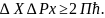
Берілген
теңдеуді Гейзенбергтің анықталмаушылық
қатынасы деп атайды. Бұдан координатасын
дәл анықтасақ импульстің белгілі мәні
болмайды және керісінше. Сөйтіп элементар
бөлшектердің орны мен импульсін бір
мезгілде мәндері болмайды. Үш
координаталары бойынша жазсақ
 .
Сонымен
қатар уақыт пен энергияның анықталмаушылық
қатыстары да қарастырылады, яғни
.
Сонымен
қатар уақыт пен энергияның анықталмаушылық
қатыстары да қарастырылады, яғни
 ,
бұл
белгілі жүйфені орташа өмір сүруі
уақыты болса, онда оны сипаттайтын
энергияны дәл өлшеуге мүмкін емес
немесе керісінше.
,
бұл
белгілі жүйфені орташа өмір сүруі
уақыты болса, онда оны сипаттайтын
энергияны дәл өлшеуге мүмкін емес
немесе керісінше.
60 Механикалық тербелістер. Математиткалық маятниктің тербеліс периодын қорыту.
Тербеліс – белгілі бір дәрежеде уақыт бойынша қайталанып отыратын процестер. Тербелістер: механикалық, электромагниттік, электромеханикалық боп бөлінеді.
Математикалық мамятник – салмақсыз және созылмайтын жіпке ілінген, массасы бір нүктеге жинақталған жүйе.
![]() Маятникті
тепе теңдік қалпынан аутқыған кезде
шама жағынан mglsin
Маятникті
тепе теңдік қалпынан аутқыған кезде
шама жағынан mglsin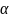 тең айналдырушы күш моменті пайда
болады. Мұндағы m – маятниктің массасы,
l – жіптің ұзындығы.
тең айналдырушы күш моменті пайда
болады. Мұндағы m – маятниктің массасы,
l – жіптің ұзындығы.
M
= -mglsin
«-»
таңбасы күш моменті мен бұрыштық ығысуы
қарама қарсы. Айналмалы қозғалыс
динамикасының негізгі теңдеуінен I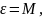 инерция моменті I=ml2
, бұрыштық үдеуін
инерция моменті I=ml2
, бұрыштық үдеуін
 деп белгілесек m
деп белгілесек m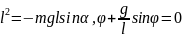 аутқу
өтое аз болғандықтан sin
=
,
олай болса
аутқу
өтое аз болғандықтан sin
=
,
олай болса
 деп белгілесек
деп белгілесек
 теңдеуі аламыз. Бұл гармоникалық
тербелістің теңдеуі. Шешімі
=cos(wt+
теңдеуі аламыз. Бұл гармоникалық
тербелістің теңдеуі. Шешімі
=cos(wt+ периоды
Т=2П
периоды
Т=2П