МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

КРЕМЕНЧУЦЬКИЙ Національний УНІВЕРСИТЕТ

ІМЕНІ михайла остроградського

ІНСТИТУТ ЕЛЕКТРОМЕХАНІКИ, ЕНЕРГОЗБЕРЕЖЕННЯ І систем управління

МЕТОДИЧНІ ВКАЗІВКИ

ЩОДО ВИКОНАННЯ РОЗРАХУНКОВОї роботи (КОНТРОЛЬНОЇ РОБоти) З НАВЧАЛЬНОЇ ДИСЦИПЛІНИ

“математичні основи цифрових систем керування”

ДЛЯ СТУДЕНТІВ денної та заочної ФОРМ НАВЧАННЯ

за напрямом

6.050201 – “Системна інженерія”

(у тому числі скорочений термін навчання)

КРЕМЕНЧУК 2011

Методичні вказівки щодо виконання розрахункової роботи (контрольної роботи) з навчальної дисципліни “Математичні основи цифрових систем керування” для студентів денної та заочної форм навчання за напрямом 6.050201 – “Системна інженерія” (у тому числі скорочений термін навчання)

Укладач: асист. Г. О. Гаврилець

Рецензент к.т.н., доц. А. Л. Перекрест

Кафедра систем автоматичного управління та електропривода

Затверджено методичною радою Кременчуцького національного університету

імені Михайла Остроградського

Протокол №____ від__________

Заступник голови методичної ради______________ доц. С. А. Сергієнко

ЗМІСТ

Вступ 4

1. Рекомендації щодо написання та оформлення розрахункової роботи (контрольної роботи) 5

2. Рекомендації щодо виконання роботи 6

Задача 1 Визначення передавальних функцій та аналіз систем керування 6

Задача 2 Отримання різницевих рівнянь за диференційними рівняннями системи та їх розв’язок за рекурентними співвідношеннями 11

Задача 3 Визначення дискретної передавальної функції імпульсної системи з екстраполятором нульового порядку 14

Задача 4 Визначення оригіналу решітчастої функції за відомим z-перетворенням 17

Задача 5 Розв’язування різницевих рівнянь 18

Список літератури 21

Додаток А Зразок оформлення титульної сторінки розрахункової роботи (контрольної роботи) 22

ВСТУП

Дисципліна “Математичні основи цифрових систем керування” вивчає питання, що стосуються математичного опису систем автоматичного керування.

Метою вивчення дисципліни є засвоєння принципів перетворення та обробки сигналів; вивчення математичного апарату для дослідження безперер­вних і дискретних систем; основ моделювання систем керування.

Дисципліна “Математичні основи цифрових систем керування” є підґрунтям дисциплін, що вивчають загальні та прикладні питання автоматичного керування технологічними об’єктами.

Метою розрахунково-графічної роботи виконання практичних робіт є закріплення студентами теоретичних знань і отримання практичних навичок при дослідженні систем керування, а також для подальшого вивчення дисциплін напряму підготовки “Системна інженерія”: теорії автоматичного керування; комп’ютеризованих систем управління; методів оптимізації керуючих алгоритмів; основ збору, передачі й обробки інформації; математичного моделювання процесів та систем.

1 Рекомендації щодо написання та оформлення розрахункової роботи (контрольної роботи)

Пояснювальна записка до роботи пишеться українською або російською мовою на аркушах формату А4 без рамок або виконується на комп’ютері. Вимоги до оформлення роботи:

Обсяг роботи – до 10 сторінок (включаючи рисунки і літературу). Заповнення сторінки не менш ніж на 80 %.

Стиль тексту – формат аркуша – А4, поля зліва – 3 см, справа – 1 см, зверху та знизу по 2 см. Інтервал між рядком – одинарний, шрифт Times New Roman, 14 pt, звичайний, абзац 1,25 см, вирівнювання по ширині, автоматичне виставлення переносів.

Стиль формул: для редактора формул наступні параметри: великі, малі грецькі літери та символи – шрифт Symbol, інші Times New Roman. Розміри: звичайний 14 pt, крупний індекс 10 pt, дрібний індекс 9 pt, крупний символ 16 pt, дрібний символ – 14 pt.

Сторінки роботи нумерують арабськими цифрами внизу посередині зі збереженням наскрізної нумерації всього тексту. Титульну сторінку теж включають до нумерації, але номер сторінки не ставлять.

Усі рисунки повинні бути пронумеровані, мати пояснювальний напис і посилання в тексті записки.

Робота містить 25 варіантів завдань. Вибір варіанту роботи здійснюється за двома останніми цифрами номера залікової книжки. Якщо отримане число N  25, то номер варіанту V = N. Якщо N більше 25, але менше 50, то V = N - 25. Якщо N більше 50, але менше 75, то V = N - 50. Якщо N більше 75, то V = N - 75.

У роботі потрібно знайти розв’язок п’яти задач, які стосуються математичного опису та аналізу цифрових систем керування.

2 Рекомендації щодо виконання роботи

Задача 1 Визначення передавальних функцій та аналіз систем керування

Система керування описується диференційним рівнянням виду:

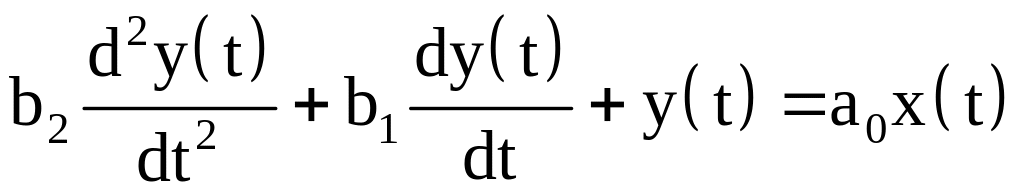(1.1)

Відповідно до варіанту (таблиця 3.1):

а) записати передавальну функцію системи за Лапласом;

б) знайти вираз для перехідної характеристики системи;

в) побудувати перехідну характеристику системи на інтервалі часу ;

г) знайти вираз для перехідної характеристики системи, використовуючи команди символьного процесора MathCAD та побудувати її графік;

д) виконати моделювання системи керування у пакеті MatLab та отримати графік перехідної характеристики. Час моделювання системи ;

е) порівняти результати, отримані розрахунковим способом і у математичних пакетах.

Таблиця 3.1 – Варіанти завдань до задачі 1

№ вар				, с	№ вар				, с
	0,6	3,2	1	20	14	0,11	0,8	1,45	4,6
	0,12	0,95	1,5	4,5	15	0,034	0,55	1,22	5,2
	0,035	0,57	1,2	4	16	0,125	0,85	2,1	5
	0,105	0,89	2	5	17	0,19	2,05	1,68	10
	0,2	2,1	1,7	10	18	0,24	1,22	2,4	6,5
	0,27	1,2	2,5	6	19	0,027	0,45	1	5
	0,025	0,55	1	4	20	0,04	0,47	1,1	4
	0,043	0,42	1,06	3	21	0,09	0,88	2,2	5
	0,096	0,92	2,3	5	22	0,023	0,66	1,7	5
	0,026	0,69	1,7	5	23	0,017	0,31	1,5	5
	0,012	0,33	1,45	4,5	24	0,37	1,15	2,3	8
	0,35	1,2	2,6	8	25	0,03	0,64	1,5	5
	0,65	3,1	1,1	20

Приклад до задачі 1. Розв’язати задачу 1, якщо система описана наступним диференційним рівнянням:

.

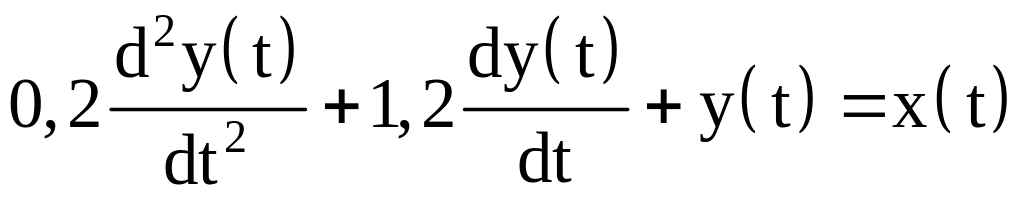Час моделювання с.

З урахуванням властивостей перетворення Лапласа:

• властивість лінійності: L{x₁(t) +x₂(t)} = L{x₁(t) + L{x₂(t)};

• диференціювання оригіналу (за нульових початкових умов):

запишемо рівняння в операторній формі:

,

.

Передавальна функція за Лапласом дорівнює відношенню зображення вихідної величини до зображення вхідної величини за нульових початкових умов:

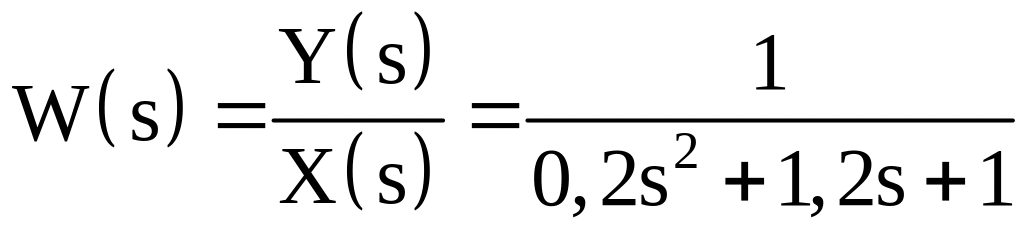. (1.2)

Передавальна функція W(s) та часові функції системи – перехідна характеристика h(t) та імпульсна перехідна функції w(t) пов'язані між собою:

L{h(t)} = W(s)/s  зображення перехідної функції;

L{w(t)} = W(s)  зображення імпульсної перехідної функції.

Звідси, відповідно, можна записати:

w(t) = L^-1{W(s)}, (1.3)

h(t) = L^-1 {W(s)/s}. (1.4)

Співвідношення (1.3), (1.4) дозволяють знайти перехідну та імпульсну перехідну функції САК за її відомою передавальною функцією W(s). Для цього можуть бути використані таблиці зображень основних елементарних функцій або теорема розкладу.

Відповідно до 1.4:

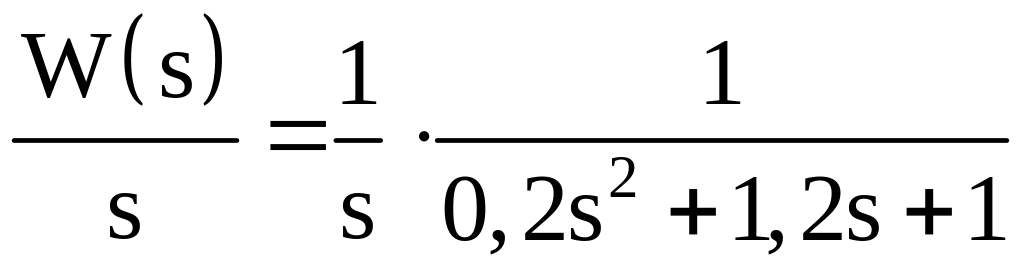, (1.5)

. (1.6)

Для знаходження зворотного перетворення Лапласа необхідно розкласти вираз (1.5) на суму простих дробів. Знайдемо корені знаменника передавальної функції і розкладемо його на множники. Отримаємо вираз:

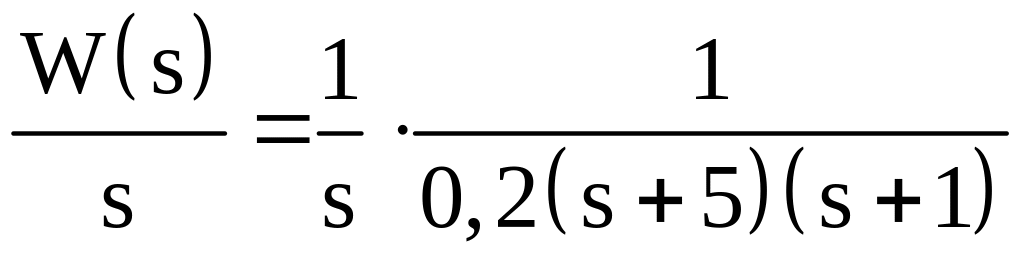
Розкладемо на суму простих дробів:

,

.

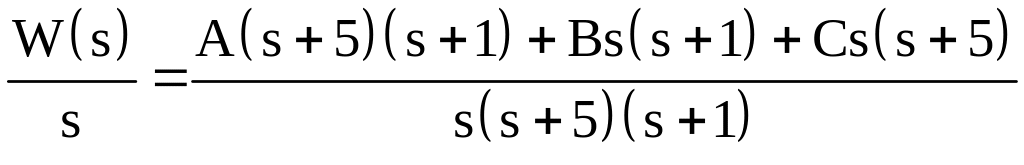Розкриємо дужки у чисельнику, згрупуємо коефіцієнти при і запишемо систему рівнянь:

А=1

В=0,25

С=-1,25

Тоді (1.5) запишемо:

. (1.7)

Знайдемо зворотне перетворення Лапласа для виразу (1.7):

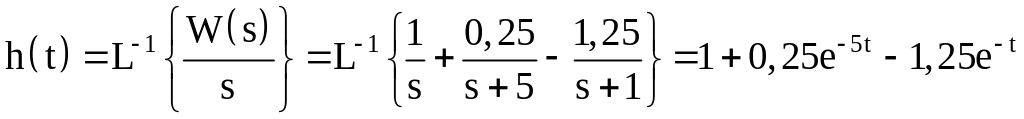(1.8)

Побудуємо графік перехідної характеристики у математичному пакеті MathCAD (рисунок 3.1):

Рисунок 3.1 – Перехідна характеристика системи у програмі MathCAD

Спростити розрахунки можна, скориставшись командами символьного процесора MathCAD, а саме:

1. factor – розклад на множники:

2. parfrac – розклад на прості дроби:

3. invlaplace – обернене перетворення Лапласа:

Отримати графік перехідної характеристики системи можна і без виконання розрахунків – шляхом моделювання у пакеті Simulink MatLab. Передавальну функцію (1.2) у Simulink представимо блоком Transfer Fcn бібліотеки Continuous, на її вхід подамо одиничну ступінчату функцію – блок Step бібліотеки Sources, а вихід з’єднаємо із блоком Scope бібліотеки Sinks (рисунок 3.2).

Рисунок 3.2 – Схема моделювання системи керування

Запустивши модель на виконання, отримаємо графік перехідної характеристики системи (рисунок 3.3).

Рисунок 3.3 – Перехідна характеристика системи у програмі Simulink

Останній спосіб найпростіший, але дає змогу лише переглядати результат, тоді як звичайний спосіб розрахунку з використанням програми MathCAD дозволить знайти розв’язок у вигляді аналітичної залежності.