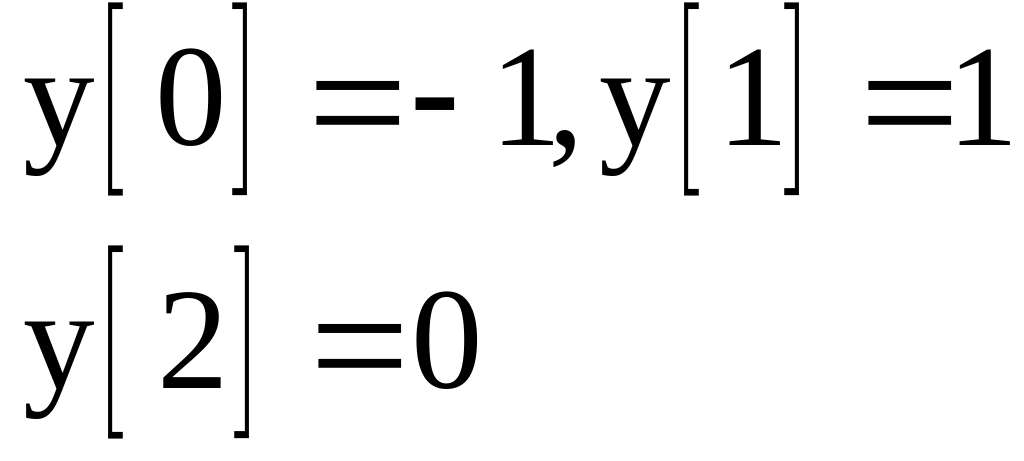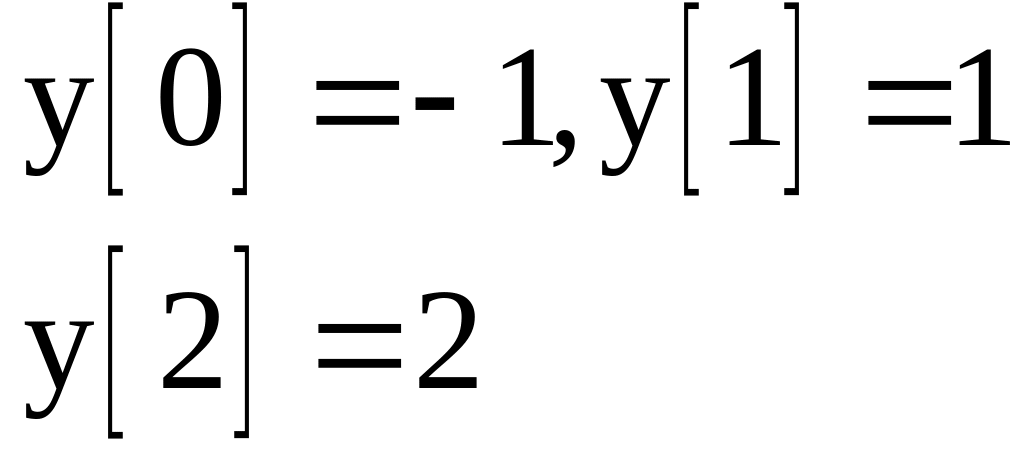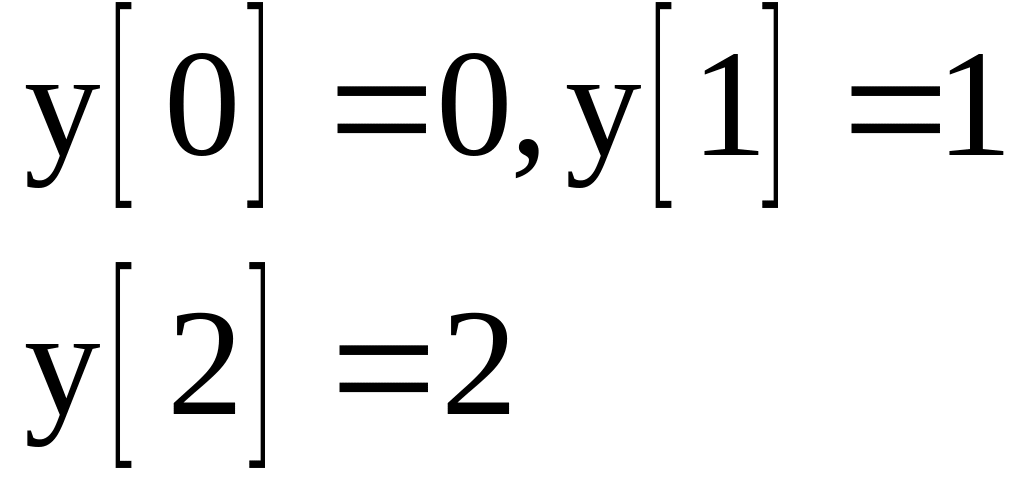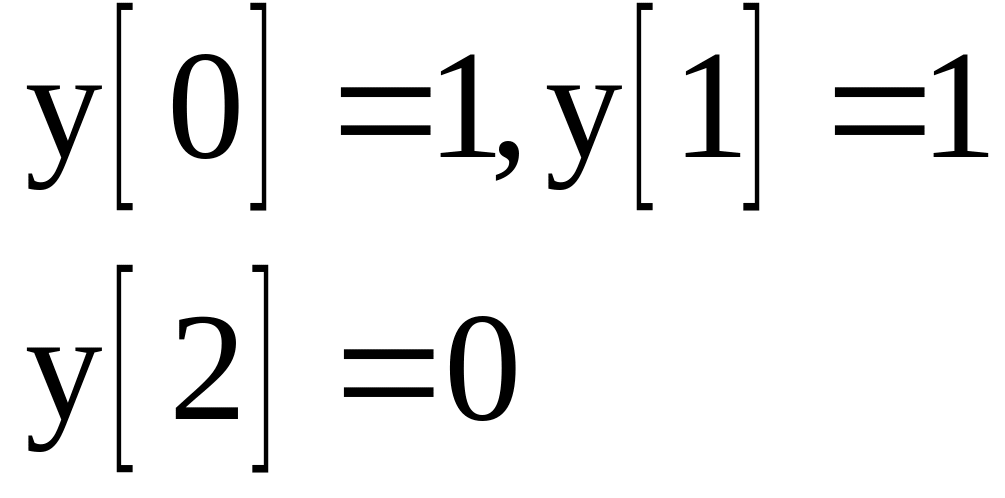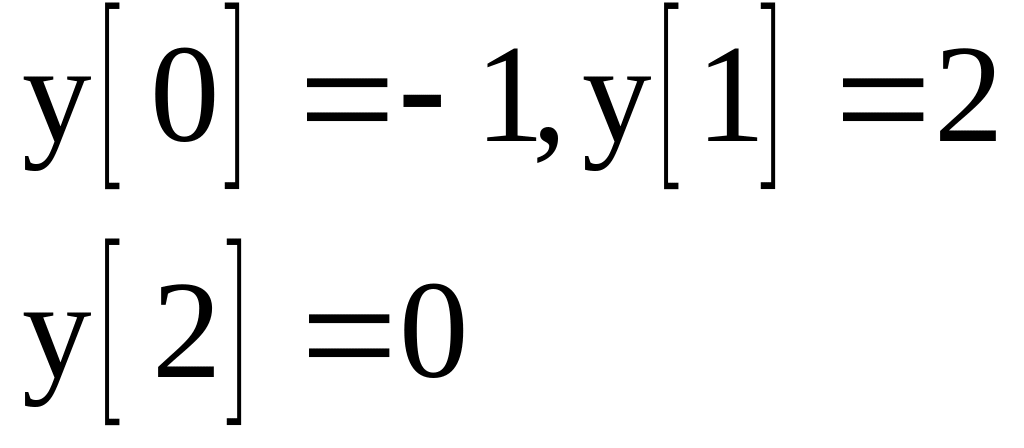Порядок виконання роботи

1. Знайти розв’язок лінійного різницевого рівняння на інтервалі на прикладі рівняння другого порядку при початкових значеннях .

Запишемо рівняння відносно :

.

1.1 Відкрити MatLab . Створити нову модель.

1.2 Розмістити на моделі такі елементи: Sources→Constant, Ports&Subsystems→ Subsystem, Signal Routing→Mux, Sinks→To Workspace.

1.3 Відкрити блок Subsystem. Створити схему розв’язку рівняння відносно (рисунок 5.4). Входи схеми In1, In2 відповідають сигналам і , виходи Out1, Out2 – і відповідно.

1.4 Створити ще 11 копій блоку Subsystem і розмістити елементи як показано на рисунку 5.5. У змінну y (формат збереження Array) записати розв’язки рівняння на кожній ітерації.

Рисунок 5.4 – Блок Subsystem

Рисунок 5.5 – Схема моделювання різницевого рівняння на інтервалі

1.5 Виконати моделювання системи. Отримати розв’язок рівняння (рисунок 5.6) за допомогою команди plot:

plot(y(1,1:13));

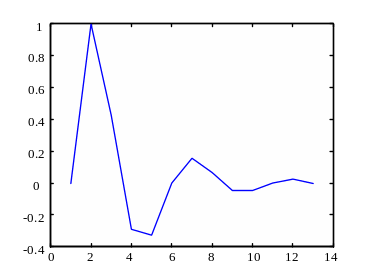
Рисунок 5.6 – Розв’язок різницевого рівняння на інтервалі

2. Знайти розв’язок лінійного різницевого на інтервалі на прикладі рівняння другого порядку при початкових значеннях . Для знаходження розв’язку на досить великому інтервалі доцільно запрограмувати дії, що повторюються згідно з алгоритмом розв’язку рівнянь як рекурентних відношень.

2.1 Скласти схему моделювання, як показано на рисунку 5.7.

Рисунок 5.7 – Схема моделювання різницевого рівняння з використанням програми

2.2 Для отримання розв’язку на інтервалі написати m-скрипт наступного змісту:

x0n=0; % початкове значення x0

x0=0; % значення x0 на першій ітерації

x1n=1; % початкове значення x1

x1=1; % значення x1 на першій ітерації

N=30; % кількість ітерацій

sim('lab5_1'); % моделювання системи

n=length(xn); % у змінній n довжина масиву xn

for i=3:N % цикл

sim('lab5_1');

y1(i)=xn(n,:); % в і-й елемент масиву y заноситься останній елемент

% масиву xn

x0=x1; % перепризначення вхідних змінних

x1=xn(n,:);

end

y1(1)=x0n; % ініціалізація перших двох елементів масиву y1

% початковими значеннями

y1(2)=x1n;

plot(y1(1,1:N)); % графічний розв’язок рівняння

2.3 Запустити скрипт на виконання, увівши у командному рядку його ім’я (без розширення). Отримати графічний розв’язок рівняння (рисунок 5.8).

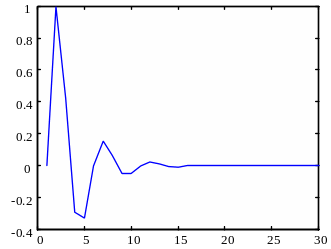
Рисунок 5.8 – Розв’язок різницевого рівняння на інтервалі

3. Відповідно до варіанту, вказаного викладачем, (таблиця 5.1) знайти розв’язок лінійного різницевого рівняння наведеними вище способами. Для першого способу знайти розв’язок на інтервалі , для другого – на інтервалі .

Таблиця 5.1 – Варіанти завдань

№ вар	Різницеве рівняння	Початкові значення

Продовження таблиці 5.1

Зміст звіту

1. Титульна сторінка.

2. Мета лабораторної роботи.

3. Пункти виконання роботи відповідно до варіанту, з представленням результатів та коментарями.

4. Висновки з роботи