
-
Контрольна робота з теорії ймовірностей
Варіант 9
Завдання 1.
Два стрільці зробили по одному пострілу по мішені. Ймовірність попасти в мішень при одному пострілі для першого стрільця дорівнює 0,8, для другого – 0,9. Яка ймовірність, що попаде лише один стрілець?
Розв'язок
Позначимо події: А1 – перший стрілець попав у мішень; А2 – другий стрілець попав у мішень. Тоді протилежні події Ā1, Ā2 означають, що відповідний стрілець не попав у мішень.
Попадання лише одного стрільця у мішень означає, що або перший стрілець попав, а другий не попав, або другий стрілець попав, а перший не попав. Позначимо подію, що в мішень попав лише один стрілець, В. Тоді за формулою складання та множення ймовірностей маємо:
Р (В) = Р (А1) • Р (Ā2) + Р (А2) • Р (Ā1)
За умовою задачі, Р (А1) = 0,8; Р (А2) = 0,9. За правилом визначення імовірності протилежних подій, маємо:
Р (Ā1) = 1 – Р (А1) = 1 – 0,8 = 0,2
Р (Ā2) = 1 – Р (А2) = 1 – 0,9 = 0,1
Отже, ймовірність того, що у мішень попаде лише один стрілець, дорівнює:
Р (В) = 0,8 • 0,1 + 0,9 • 0,2 = 0,08 + 0,18 = 0,26
Завдання 2.
В ящику міститься 12 деталей, виготовлених на заводі № 1 і 20 деталей, виготовлених на заводі № 2. Імовірність того, що деталь, виготовлена на заводі № 1 стандартна, дорівнює 0,8, для деталей, виготовлених на заводі № 2, ця ймовірність дорівнює 0,7. Яка імовірність, що взята навмання деталь стандартна?
Розв'язок
Нехай подія А означає, що взята навмання деталь стандартна. Позначимо події: Н1 – деталь виготовлена на заводі № 1, Н2 – деталь виготовлена на заводі № 2. Позначимо умовні імовірності РН1(А), РН2(А) – деталь є стандартною при умові, що вона виготовлена відповідно на заводі № 1 та № 2. За умовою задачі, ці імовірності дорівнюють: РН1(А) = 0,8; РН2(А) = 0,7
Визначаємо імовірності подій Н1 та Н2:
12 12
Р(Н1) = –––––– = –––– = 0,375;
12 + 20 32
20 20
Р(Н2) = –––––– = –––– = 0,625;
12 + 20 32
За формулою повної імовірності визначаємо імовірність того, що взята навмання деталь є стандартною:
Р (А ) = РН1(А) • Р(Н1) + РН2(А) • Р(Н2) = 0,8 • 0,375 + 0,7 • 0,625 =
= 0,3 + 0,4375 = 0,7375.
Завдання 3.
Проведено n = 900 незалежних випробувань, в кожному з яких може відбутись подія А з імовірністю р = 0,8.
а) За локальною теоремою Муавра – Лапласа знайти імовірність того, що подія А наступить 709 раз.
б) За інтегральною теоремою Муавра – Лапласа знайти імовірність того, що подія А наступить від 700 до 729 раз.
Розв'язок
а) За локальною теоремою Муаврв – Лапласа, ймовірность того, що у n незалежних випробуваннях подія А відбудеться m разів визначається за формулою:
1 m – nр

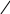


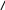
 Рn
(m)
= –––––––– •
φ ( ––––––– )
Рn
(m)
= –––––––– •
φ ( ––––––– )
npq npq
де р – імовірність того, що подія А відбудеться у кожному окремому незалежному випробуванні
q = 1 – р - імовірність того, що подія А не відбудеться у кожному окремому незалежному випробуванні
1
φ (х) = ––––– • ( е – t²/ 2 ) –функція Гаусса
2 π
m – nр
х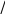
 = –––––––
= –––––––
npq
Визначаємо х :
709 – 900 · 0,8 709 – 720 – 11
х
 = –––––––
––––––
= –––––––– = –––––– = – 0,92
= –––––––
––––––
= –––––––– = –––––– = – 0,92
900 · 0,8 · 0,2 144 12
За таблицею значень функції Гаусса і враховуючи парність функції, визначаємо, що φ (– 0,92) = 0,2613
Звідси, ймовірність того, що що подія А наступить m = 709 раз, становить:
1 1
Р900 (709) = –––––––– • φ ( – 0,92 ) = –––– • 0,2613 = 0,0218
144 12
б) За інтегральною теоремою Муавра-Лапласа, ймовірность того, що у n незалежних випробуваннях подія А відбудеться від m1 до m2 разів визначається за формулою:
m2 – nр m1 – nр
Рn (m1 ≤ m ≤ m2) = Ф ( ––––––– ) – Ф ( ––––––– )
npq npq
де р – імовірність того, що подія А відбудеться у кожному окремому незалежному випробуванні
q = 1 – р - імовірність того, що подія А не відбудеться у кожному окремому незалежному випробуванні
1 х
Ф (х) = ––––– ∫ е – t²/ 2 dt –функція Лапласа
2 π 0
m1 – nр m2 – nр
х 1 = –––––––; х 2 = –––––––;
npq npq
Визначаємо х1 та х2 :
700 – 900 · 0,8 700 – 720 – 20
х 1 = ––––––– –––––– = –––––––––– = –––––– = – 1,67
900 · 0,8 · 0,2 144 12
729 – 900 · 0,8 729 – 720 9
х
 2
= –––––––
––––––
= ––––––––– = ––– = 0,75
2
= –––––––
––––––
= ––––––––– = ––– = 0,75
900 · 0,8 · 0,2 144 12
За таблицею значень функції Лапласа і враховуючи непарність функції, визначаємо, що Ф (– 1,67) = – 0,4526; Ф (0,75) = 0,2735.
Звідси, ймовірність того, що не подія А наступить від m1 = 700 до m2 = 729 раз становить:
Р900 (700 ≤ m ≤ 729) = Ф (0,75) – Ф (– 1,67) = 0,2735 + 0,4526 = 0,7261
