- •Введение
- •Правила техники безопасности при выполнении лабораторных работ
- •Лабораторная работа №1 Тема: Опытная проверка свойств последовательного соединения резисторов
- •Основные теоретические положения
- •Обьект и средства исследования
- •Порядок проведения эксперимента
- •Контрольные вопросы и задачи
- •Литература:
- •3.В.М. Прошин Лабораторно-практические работы по электротехнике-2009г.
- •Лабораторная работа №2
- •Основные теоретические положения
- •Обьект и средства исследования
- •Порядок проведения эксперимента
- •Обработка результатов эксперимента
- •Контрольные вопросы и задачи
- •Тема: Расчет электрических цепей при смешанном соединении резисторов Время : 6 час
- •Величина тока в последовательной цепи
- •Распределение напряжения в последовательной цепи
- •Сумма напряжений на участках последовательной цепи равна напряжению источника тока
- •Общее сопротивление параллельно включенных сопротивлений определяется по формуле:
- •Распределение токов и напряжения в параллельных ветвях
- •Лабораторная работа №3 Тема: опытная проверкасвойств параллельного соединения конденсаторов Время-2 час
- •Общие положения
- •Описание экспериментальной установки
- •Параллельное
- •Порядок выполнения работы Задание 1 Определение постоянной установки
- •Задание 2 Определение емкости конденсатора
- •Задание 3 Измерение емкости параллельно и последовательно соединенных конденсаторов
- •Контрольные вопросы и задания
- •3.Что такое смешанное соединение резисторов?
- •4.По какому методу легче решать задачи по данным схемам?
- •1. Исследовать явление резонанса напряжений.
- •Объект и средства исследования
- •Порядок проведения эксперимента
- •Обработка результатов эксперимента
- •Контрольные вопросы и задачи
- •Лабораторная работа №5.
- •Введение
- •Порядок выполнения работы и обработка результатов измерения
- •Лабораторная работа№7 Тема "исследование трехфазной четырепроводной электрической цепи синусоидального тока
- •2. Каково соотношение между фазными и линейными напряжениями и токами при соединении нагрузки "звездой"?
- •5. Что такое напряжение смещения нейтрали? в каких случаях оно равно нулю?
- •6.Чем опасно короткое замыкание одной фазы при наличии и отсутствии нулевого провода?
- •Контрольные вопросы:
- •Тема: Испытание однофазного трансформатора Время-4 час
- •Содержание
- •Порядок выполнения работы
- •Рекомендации по обработке экспериментальных данных
- •1. Опыт холостого хода.
- •2. Опыт короткого замыкания.
- •3. Опыт нагрузки.
- •7. Содержание отчета
- •Содержание графической части и выводов
- •Контрольные вопросы
- •Техника безопасности при испытании трансформатора
- •Лабораторная работа №11 Тема: Определение потерь напряжения в линиях электропередач
- •1.Пояснение к работе
- •2.Техническое задание
- •3.Работа в лаборатории.
- •4. Содержание отчета
- •5.Контрольные вопросы.
- •Лабораторная работа №12 Тема: Исследование и снятие вольт-амперных характеристик полупроводникового диода
- •Общие сведения
- •Задание
- •Описание лабораторной установки
- •Указания по выполнению работы
- •Содержание отчета
- •Контрольные вопросы
- •Содержание
- •Очевидно, примесная фотопроводимость возникает при условии
- •Методика эксперимента с хематическое устройство фоторезистора дано на рис.3.
- •Введение к выполнению работы
- •Задание к работе.
- •Отчет Контрольные вопросы
- •Задание
- •Предварительная подготовка
- •Работа в лаборатории
- •Содержание отчета
- •Контрольные вопросы
R
I
Рис. 7
V
R
I
Напряжение на некотором участке электрической цепи имеряется вольтметром, который подключается параллельно тому участку цепи, на котором измеряется напряжение (рис.7). Вольтметр имеет очень большое внутреннее сопротивление поэтому его подключение не влияет на режим работы цепи.
Рис.
8
R
Обьект и средства исследования
Объектом исследования является последовательная цепь, состоящие из резисторов R1–R4 смонтированных на плате № 4.
Источником питания служит источник постоянного тока с регулируемой величиной ЭДС. Выходные гнезда источника расположены на центральной панели стенда и обозначены ‘+’ и ‘-‘ Внутреннее сопротивление источника не учитывается, т. е. источник ЭДС полагается идеальным.
В качестве электроизмерительных приборов используются многопредельные миллиамперметры Э377, а так же цифровой или стрелочный многопредельный электронный вольтметр. Выбор предела измерения миллиамперметра осуществляется нажатием одной из клавиш, размещенных под прибором. Цифра под клавишей указывает предел измерении (ПИ) в миллиамперах.
Тогда, для того, чтобы определить значение тока по отклонению стрелки (ОС) необходимо:
вычислить цену деления (цд) прибора ЦД=ПИ/КДП, отметим, что для миллиамперметров Э377 количество делений прибора (КДП) равно 100;
вычислить ток в амперах [ I ]=1000*ЦД*ОС.
Порядок проведения эксперимента
1.Собрать с помощью монтажной схемы (рис.9) последовательную цепь в соответствии с рисунком 10.










Рис. 9
f
e
c
b
a
V
R1
R2
R4
R3
+
-
А
После проверки цепи преподавателем подать на неё напряжение, для чего:
на плате рис9. лицевой панели стенда поставить тумблер ВЗ-1 в положение "Вкл.", а тумблер В3-2 - в положение II;
включить тумблеры В1 и Â2 на центральной панели стенда.
3. Подключив вольтметр к гнёздам а и f , с помощью ручки "Рег. Uвх" на плате № 3 установить указанную преподавателем величину напряжения U af и записать ее в табл. 1.
4. Записать в табл. 1 показания амперметра, измеряющего ток I в цепи.
5. Измерить с помощью вольтметра напряжения на каждом резисторе R1 и R4, а также Uaf и записать их значения а табл. 1.
6. Снять напряжение, отключив тумблеры В1 и В2 и отсоединить цепь от гнезд "+" и "-" источника питания.
Используя электронный измерительный прибор в режиме омметра измерить сопротивление каждого резистора, а также Raf . Результаты записать в табл. 1.
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
1. Используя закон Ома, рассчитать значение сопротивлений R1, R2, R3, R4 и Raf Результаты занести в табл. 2.
2. Вычислить мощность на каждом резисторе и мощность всей цепи. Результаты занести в табл. 2.
Расчетным путем определить ток I и напряжения на каждом резисторе U1-U4 , считая известным напряжение Uaf и сопротивления R1-R4 (значения Uaf и R1-R4 взять из табл. 1).
4. Сравнить результаты измерений и расчетов, сделать выводы.
Контрольные вопросы и задачи
1. Дать определение электрической цепи.
2.Что называется последовательным и параллельным соединением? Привести примеры.
3. Сформулировать закон Ома и законы Кирхгофа.
4. Êàê связаны общее напряжение, приложенное к последовательной цепи, с напряжениями на каждом элементе цепи?
5. Как зависит эквивалентное сопротивление последовательной цепи от сопротивлений ее элементов?
6. Как изменится напряжение U2 (рис. 5), если уменьшить сопротивление R3, при постоянном значении U ?
7. Как изменится напряжение U2 (рис. 5), если уменьшить сопротивление R2 при постоянном значении U ?
Определить напряжение между точками b и e (рис.9), если U=100 В, R1=10 0м, R2=15 0м, R3= 20 0м, R4=5 Ом.
Литература:
1.М.В.Немцов,И.И.Светлакова Электротехника-2008г.
2.Л.И.Фуфаева Электротехника-2009г.
3.В.М. Прошин Лабораторно-практические работы по электротехнике-2009г.
приложение
ПРОТОКОЛ ИСПЫТАНИЙ
К лабораторной работе ¹1. Исследование линейных электрических цепей постоянного тока с последовательным соединением резисторов.
Рис.
10
Uaf
a
А
R1
R2
R4
R3
b
c
e
f

Измеренные параметры |
Участок цепи |
||||
параметры |
аb |
bс |
се |
ef |
af |
U, В |
|
|
|
|
|
I, А |
|
|
|
|
|
R, Oì |
|
|
|
|
|
РАСЧЁТНО-ГРАФИЧЕСКАЯ ЧАСТЬ
Таблица 2
Рассчитанные |
Участок цепи |
||||
параметры |
аb |
bс |
се |
ef |
af |
R, Oì |
|
|
|
|
|
Р, Вт |
|
|
|
|
|
Расчётные формулы:
Расчет последовательной цепи.
Дано: Определить:
Расчет:
Краткие выводы по работе:
Группа _______ Студент ________ «__» _______ 199__ г.
Преподаватель__________________________
Лабораторная работа №2
Тема: ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ РЕЗИСТОРОВ.
Время-2 час
Цель работы:
1. Приобрести навыки сборки параллельных электрических цепей.
2. Закрепить навыки пользования электроизмерительными приборами.
3. Закрепить теоретические сведения о методах анализа электрических цепей с параллельным соединением резисторов (потребителей).
Основные теоретические положения
Рис.
1
R3
I3
R1
I1
I2
U
R2
I
При параллельном соединении общий ток цепи I , т.е. ток, проходящий через источник, связан с токами I1, I2 и I3 первым законом Кирхгофа
I=I1+I2+ I3.
 При
анализе Параллельной цепи удобно
пользоваться понятием проводимости G,
являющейся величиной, обратной
сопротивлению, т.е,
При
анализе Параллельной цепи удобно
пользоваться понятием проводимости G,
являющейся величиной, обратной
сопротивлению, т.е,
G=1/R
Единица измерения проводимости - Сименс (См).
В соответствии с законом Ома проводимости каждой из ветвей G1, G2 и G3 (рис. 1) определяются формулами
G1=I1/U=1/R1, G2=I2/U=1/R2, G3=I3/U=1/R3,
тогда, эквивалентная проводимость всей цепи Gэк находится как сумма проводимостей всех параллельных ветвей цепи
Gэк=I/U=G1+G2+G3.
Из последней формулы легко получить выражение для эквивалентного сопротивления цепи, представленной на рисунке 1:
RЭК=R1R2R3/(R1R2+R2R3+R1R3),
а, для цепи из двух параллельных элементов
RЭК=R1R2/(R1+R2).
Если ветвь состоит из двух или более последовательно соединенных элементов, то ее проводимость определяется согласно формуле
G=1/(R1+ R2+...+ RN),
где N – число элементов ветви.
Характерной особенностью параллельной цепи является то, что режим работы любой ветви не зависит от параметров других ветвей, поэтому параллельное соединение является основным способом подключения потребителей к электрической сети .
 Активная
мощность Р всей цепи определяется по
одному из следующих выражений:
Активная
мощность Р всей цепи определяется по
одному из следующих выражений:
P=UI , Р=I2RЭК= I2/GЭК, Р=U2/RЭК= U2GЭК.
При заданной величине напряжения U, приложенной к цепи, ее анализ сводится и расчету тока каждой из ветвей в отдельности (рис. 1), т.е.
I1=U/R1=UG1, I2=U/R2=UG2, I3=U/R3=UG3,
и определению общего тока I по первому закону Кирхгофа.
Если известны величины общего тока I и сопротивление всех элементов, то рассчитывать данную цепь необходимо в следующем порядке:
вычислить проводимости каждой ветви;
определить эквивалентную проводимость цепи;
по известному значению тока I в соответствии с законом Ома для всей цепи найти напряжение;
рассчитать токи в. ветвях по закону Ома:
проверить правильность расчета по первому закону Кирхгофа.
Обьект и средства исследования
Объектом исследования является параллельная цепь, состоящие из резисторов, смонтированных на плате № 4.
Указанные на схеме стенда соединения выполнены при монтаже стенда. В качестве параллельной цепи берется цепь, состоящая из двух ветвей, одна из которых включает в себя последовательно соединенные R2 и R3, а другая - R5 и R6.
В качестве электроизмерительных приборов используются многопредельные миллиамперметры Э377, а так же цифровой или стрелочный многопредельный электронный вольтметр.
Порядок проведения эксперимента
1.Собрать с помощью монтажной схемы (рис.2) последовательную цепь в соответствии с рисунком 3.




R5
R6
d
d
А
А
c
Рис. 2
e
c
b
V
R2
R3
+
-
А
R2
R3
b
c
e
c
После проверки цепи преподавателем подать на неё напряжение, для чего:
R2
R3
b
c
e
c
R2
R3
b
c
e
c
на плате № 3 левой панели стенда поставить тумблер ВЗ-1 в положение "Вкл.", а тумблер В3-2 - в положение II;
включить тумблеры В1 и В2 на центральной панели стенда.
3. Подключив вольтметр к гнездам "+" и "-" источника питания, с помощью регулятора напряжение установить заданную преподавателем величину напряжения U и записать ее в таблицу 1.
4. Измерить токи в ветвях и записать их значения в таблицу 1.
Измерить напряжения на участках схемы и записать их значения в таблицу
Обесточив цепь, используя электронный измерительный прибор в режиме омметра измерить сопротивление каждого резистора, а также R be . Результаты записать в таблицу 1.
Обработка результатов эксперимента
1. Используя закон Ома, рассчитать значение сопротивлении R2, R3, R5, R6 и R be Результаты занести в табл. 2.
Вычислить мощность на каждом резисторе и мощность всей цепи. Результаты занести в табл. 2.
3. Используя закон Ома, вычислить проводимости участков цепи и эквивалентную проводимость всей цепи. Результаты записать в таб. 4.
Записать уравнение по первому закону Кирхгофа для узла "b" и проверить соответствие ему экспериментальных данных.
Записать уравнение по второму закону Кирхгофа для контура bdecb и проверить соответствие ему экспериментальных данных.
Контрольные вопросы и задачи
1.Что называется параллельным соединением? Привести примеры.
2. Сформулировать закон Ома и законы Кирхгофа.
3. Как зависит общий ток в параллельной цепи (рис. 1) от токов в ветвях?
4. Как изменится ток I2 (рис. 1), если увеличить сопротивление R3?
5. Определить ток I (рис. 3), если U=20 В, R2=10 0м, R3=30 0м, R5=15 0м, R6=5 0м.
6. Определить напряжение U, приложенное к цепи (рис. 3), а также токи I1, и I2, если I=5А, R2=10 0м, R3=10 0м, R5=20 0м, R6=10 0м.
7. При какой величине тока I (рис. 3) мощность, рассеиваемая на резисторе R5 будет равна 60 Вт, если R2=6 0м, R3=4 0м, R5=5 0м, R6=10 0м
Приложение
ПРОТОКОЛ ИСПЫТАНИЙ
К лабораторной работе №2. Исследование линейных электрических цепей постоянного тока с параллельным соединением резисторов.
Таблица 1
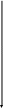
R6 R5 d А А Рис. 3 Ube А R2 R3 b c e
|
Участок цепи |
||||
параметры |
bс |
се |
bd |
de |
be |
U, В |
|
|
|
|
|
I, А |
|
|
|
|
|
R, Oì |
|
|
|
|
|
РАСЧЁТНО-ГРАФИЧЕСКАЯ ЧАСТЬ
Таблица 2
Рассчитанные |
Участок цепи |
||||
параметры |
bс |
се |
bd |
de |
be |
R, Oì |
|
|
|
|
|
G, См |
|
|
|
|
|
Р, Вт |
|
|
|
|
|
Расчётные формулы:
Расчет параллельной цепи.
Дано: Определить:
Расчет:
Краткие выводы по работе:
Группа _______ Студент ________ «__» _______ 199__ г.
Преподаватель__________________________
Практическая работа №1
Тема: Расчет электрических цепей при смешанном соединении резисторов Время : 6 час
Цель работы: опытным путем изучить законы протекания тока через последовательно и параллельно соединенные проводники и определить формулы расчета сопротивлений таких участков. 1.Пояснение к работе
Краткие теоретические сведения Последовательным соединением сопротивлений называется такое соединение, при котором конец первого сопротивления соединяется с началом второго, конец второго - с началом третьего и т. д.
Общее сопротивление последовательно соединенных резисторов равно сумме их сопротивлений. Rобщ.=R1+R2+R3 Rобщ=5ом+10ом+25ом=40ом
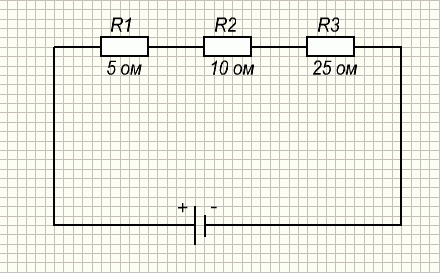
Величина тока в последовательной цепи
Так как в данной цепи отсутствует ответвление тока, то очевидно, что количество электричества, протекающее через поперечное сечение проводника за единицу времени. в любой точке цепи будет одинаковым. Следовательно во всех точках последовательной цепи величина тока одинакова. Эти четыре амперметра покажут одинаковые величины тока. Поэтому при последовательном соединении для измерения тока достаточно включать один амперметр на любом участке цепи.
Распределение напряжения в последовательной цепи

Напряжение источника тока приложенное к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков. Напряжение приложенное к каждому из этих резисторов определяется по формуле:
![]()
Так как ток в последовательной цепи везде одинаков значит действительно напряжение на ее участках зависит от сопротивления чем больше сопротивление тем большее напряжение приложено к данному участку.
Сумма напряжений на участках последовательной цепи равна напряжению источника тока
![]()
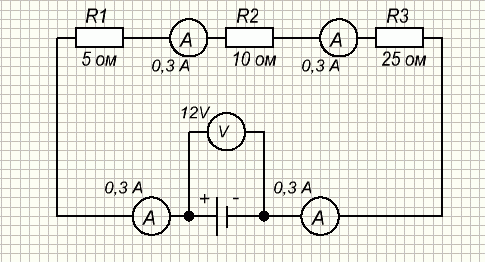
Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму - концы.
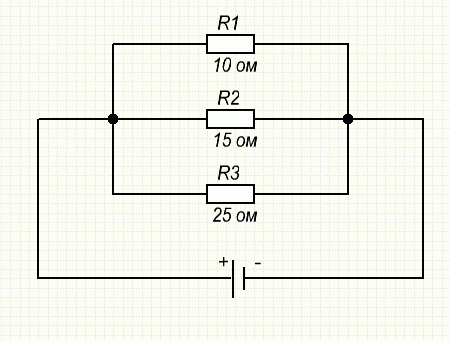
Общее сопротивление параллельно включенных сопротивлений определяется по формуле:
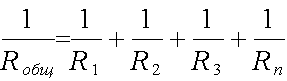
Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение. На вышеуказанном рисунке мы можем сразу сказать что общее сопротивление будет меньше 10 ом. Первый частный случай Если параллельно включено только два резистора то их общее сопротивление можно определить по формуле:
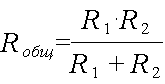
Второй частный случай
Если параллельно включено любое количество резисторов одинаковых сопротивлений то их общее сопротивление можно определить если сопротивление одного резистора разделить на количество резисторов.
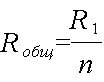
Распределение токов и напряжения в параллельных ветвях
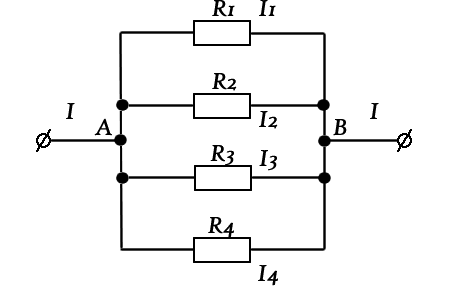
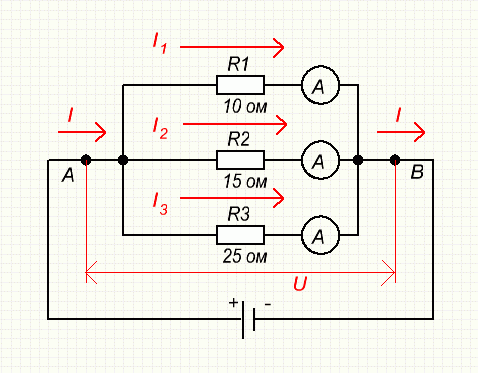
Так как начала всех сопротивлений сведены в одну общую точку, а концы - в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.
Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.
![]()
Если разветвление подключено непосредственно к зажимам источника тока, то напряжение на каждом из сопротивлений равно напряжению на зажимах источника.
![]()
Второе свойство цепи с параллельным соединением заключается в том, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям. Это значит что, чем больше сопротивление, тем меньше по нему пойдет ток.
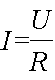
Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, I3 утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду утекающему от нее:
![]()
Следовательно, третье свойство параллельного соединения может сформулирована так: Величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.
Техническое задание Собрать электрическую цепь (рисунок 1) смешанное соединение

Рисунок 1. Схема электрическая принципиальная.
Снять показания приборов и записать их в таблицу Произвести расчеты Ответить на контрольные вопросы Сделать вывод Работа в лаборатории
Собрать схему (Рисунок 2).

Рисунок 2. Схема исследования.
Установить на схеме величины R1=1 кОм + N, R2=2 кОм + N, R3=3 кОм + N и R4=4 кОм + N, где N - номер студента по журналу (мощность резисторов более 1 Вт). Включить источник и установить напряжение U=15 В, 24 В. Определите экспериментально с помощью мультиметра (в режиме измерения сопротивлений) сопротивление между точками:
А и С; С и D; B и D; A и D.
Запишите эти показания в таблицу 1. Рассчитайте теоретические значения сопротивлений между указанными точками схемы и сравните их с измеренными. Измерьте с помощью мультиметра (в режиме измерения тока) токи, текущие через каждое сопротивление. Запишите показания прибора в таблицу 2. Проверьте экспериментально, что в последовательной цепи ток одинаков через все сопротивления, а в параллельной цепи разделяется так, что сумма всех токов через параллельно соединенные элементы, равна полному току через весь участок. Измерьте с помощью мультиметра (в режиме измерения постоянного напряжения) напряжения на каждом сопротивлении. Запишите показания прибора в таблицу 2. Проверьте экспериментально, что в последовательной цепи напряжение на всем участке равно сумме напряжений на каждом элементе, а в параллельной цепи, напряжение одно и то же на каждом элементе. Отключить схему. Таблица 1 - Рассчитанные параметры
№ вар. |
Установлено |
Рассчитано |
||||||
R1 |
R2 |
R3 |
R4 |
А - С |
С - D |
B - D |
A-D |
|
кОм |
кОм |
кОм |
кОм |
кОм |
кОм |
кОм |
кОм |
|
|
|
|
|
|
|
|
|
|
Таблица 2 - Измеренные параметры
№ изм. |
U |
I |
I1 |
I2 |
I3 |
I4 |
U1 |
U2 |
U3 |
U3 |
В |
А |
А |
А |
А |
А |
В |
В |
В |
В |
|
1 |
15 |
|
|
|
|
|
|
|
|
|
2 |
24 |
|
|
|
|
|
|
|
|
|
Содержание отчета Название и цель работы Схемы Таблицы Ответы на контрольные вопросы Вывод
Контрольные вопросы: 1. Может ли сопротивление участка двух параллельно соединенных проводников быть больше (меньше) любого из них? Объясните ответ. 2.Какие законы сохранения используются для вывода формул сопротивления параллельного и последовательного соединения проводников?
Лабораторная работа №3 Тема: опытная проверкасвойств параллельного соединения конденсаторов Время-2 час
Цель работы – определить электроёмкость неизвестного конденсатора и системы конденсаторов, соединённых последовательно и параллельно.
Приборы и принадлежности: микровеберметр, вольтметр, потенциометр, магазин сопротивлений, эталон емкости, конденсатор неизвестной емкости, источник напряжения, переключатель, выключатель.
Общие положения
Электрической емкостью уединенного проводника называется физическая величина, измеряемая отношением заряда проводника к его потенциалу. Если заряд проводника q, его потенциал φ, то по определению электроемкости
 .
(1)
.
(1)
Электроемкость зависит от размеров и формы проводников, среды,
а также от взаимного расположения окружающих тел и проводника. Система
из
двух проводников, разделенных слоем
диэлектрика называется конденсатором.
Электроемкостью конденсатора называют
величину равную отношению заряда q
к разности потенциалов
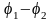 между обкладками. Обозначим
=U,
тогда
между обкладками. Обозначим
=U,
тогда

Электроемкость плоского конденсатора практически не зависит от окружающих тел и определяется выражением

где
ε – диэлектрическая проницаемость
среды, ε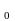 = 8, 8510
= 8, 8510 Ф/м, S
– площадь пластин, d
– расстояние между пластинами.
Ф/м, S
– площадь пластин, d
– расстояние между пластинами.
Конденсаторы можно соединять в батарею, причем при последовательном соединении (рис.1) емкость батареи рассчитывается по формуле
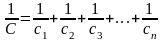 (2)
(2)
При параллельном соединении общая емкость батареи
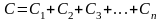 (3)
(3)
Описание экспериментальной установки
 В
данной лабораторной работе требуется
определить электроемкость каждого из
двух конденсаторов неизвестной
емкости и емкость батареи при
последовательном и параллельном
соединении конденсаторов. Для определения
емкости конденсатора необходимо знать
разность потенциалов между обкладками
конденсатора и заряд на его обкладках.
В
данной лабораторной работе требуется
определить электроемкость каждого из
двух конденсаторов неизвестной
емкости и емкость батареи при
последовательном и параллельном
соединении конденсаторов. Для определения
емкости конденсатора необходимо знать
разность потенциалов между обкладками
конденсатора и заряд на его обкладках.

Рисунок 1.
Последовательное
соединение
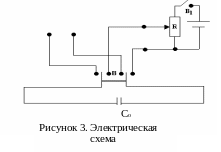
Для определения емкости конденсатора в данной работе используется установка, электрическая схема которой приведена на рис.3.
Рисунок
2. соединение
Параллельное
Если с помощью потенциометра установить определенное напряжение и зарядить конденсатор, а затем переключить конденсатор на микровеберметр, то конденсатор разрядится через него, при разрядке конденсатора возникают кратковременные токи, которые могут быть измерены с помощью цифрового микровеберметра. Инструкция по использованию микровеберметра находится на рабочем столе.
V
Микровеберметр



 Практически
заряд любого конденсатора можно
определить, разряжая через микровеберметр
конденсатор известной емкости С0,
заряженный до известной разности
потенциалов U0
Практически
заряд любого конденсатора можно
определить, разряжая через микровеберметр
конденсатор известной емкости С0,
заряженный до известной разности
потенциалов U0
 .
.
Зная заряд конденсатора q0 и показания микровеберметра n0, определяют постоянную прибора
Рисунок
3. Электрическая
схема установки
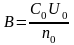 .
(4)
.
(4)
Используя значение постоянной можно определить емкость любого конденсатора по формуле
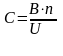
(5)
где U – разность потенциалов между пластинами конденсатора, n – показание микровеберметра.
Порядок выполнения работы Задание 1 Определение постоянной установки
1. Собрать электрическую цепь согласно схеме (рис.3).
2. Определить постоянную установки, для чего включить в цепь эталонный конденсатор С0. Замкнув выключатель В1 и передвигая контакт потенциометра, установить указанное преподавателем напряжение U0.
Установить переключатель В в положение, при котором конденсатор заряжается. Перекинуть переключатель В в положение для разрядки конденсатора через микровеберметр и снять показание n0. По формуле (4) определить постоянную установки В. Опыт следует повторить не менее пяти раз, изменяя напряжение U0 в пределах, указанных преподавателем. Данные измерений занести в составленную таблицу. Определить среднее значение постоянной.
Задание 2 Определение емкости конденсатора
1. Заменить в цепи (рис.3) эталонный конденсатор конденсатором неизвестной емкости и при трех значениях напряжения в пределах, указанных преподавателем, снять показания микровеберметра.
2. Зная
U,
B,
n,
по формуле (5) рассчитать емкость первого
конденсатора С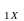 .
Повторить измерения для второго
конденсатора и определить его емкость
С
.
Повторить измерения для второго
конденсатора и определить его емкость
С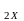 .
Результаты занести в таблицу.
.
Результаты занести в таблицу.
Задание 3 Измерение емкости параллельно и последовательно соединенных конденсаторов
1. По схеме, приведенной в задании 2, провести измерения с обоими конденсаторами Cx, включив их сначала параллельно, а затем последовательно. Сравнить результаты измерения емкости батареи конденсаторов с емкостью, вычисленной по формулам (2) и (3).
Результаты измерений внести в таблицу.
2. Расчет погрешностей произвести для каждого из конденсаторов как для прямых измерений.
Контрольные вопросы и задания
Дайте определение электрической ёмкости уединенного проводника.
Что представляет собой конденсатор? Дайте определение электроемкости конденсатора.
Поясните физический смысл электроемкости отдельного проводника и системы проводников.
Как определять электроёмкость батареи последовательно и параллельно соединённых конденсаторов?
Зачем в работе используется эталонный конденсатор?
Практическая работа №2
Тема: Расчет электрических цепей при смешанном соединении резисторов
Время-2 час.
Цель работы: Сформировать знания студентов в расчете электрических цепей при смешанном соединении резисторов и применения этих схем в электротехнике и электронике
Содержание
Смешанное соединение резисторов
Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением. На рисунке 4 показан простейший пример смешанного соединения резисторов.

Рисунок 4. Смешанное соединение резисторов.
На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно. Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму: 1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов. 2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление. 3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений. 4. Рассчитывают сопротивления полученной схемы.
Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 1.

Рисунок 1. Расчет сопротивления участка цепи при смешанном соединении резисторов.
Задания для студентов :при заданных номиналах R,I иU определить токи в ветвях? Использовать законы для последовательного и параллельного соединения резисторов.

Контрольные вопросы:
1.1- закон Кирхгофа, формулировка и формула.
2. 2-закон Кирхгофа, формулировка и формула.
3.Что такое смешанное соединение резисторов?
4.По какому методу легче решать задачи по данным схемам?
ЛАБОРАТОРНАЯ РАБОТА №4
Тема: ИССЛЕДОВАНИЕ НЕРАЗВЕТВЛЕННОЙ RLC -ЭЛЕКТРИЧЕСКОЙ ЦЕПИ СИНУСОИДАЛЬНОГО тока
Время: 6час
Цель работы.
1. Исследовать явление резонанса напряжений.
2. Установить связь между током, напряжениями на элементах цепи и емкостью конденсатора.
3. Получить навыки построения векторных диаграмм и научиться их использовать для анализа электрических цепей.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
В данной работе исследуется неразветвленная цепь, состоящая из катушки индуктивности и конденсатора, подключенная к сети синусоидального тока. Схема цепи представлена на рис. 1.
U
С
UС
L
Рис.
2
UL
R
UR
UК
I
С
UС
R,
L
Рис.
1
U
UК
I
























Индуктивный и емкостный элементы характеризуются соответственно индуктивным XL = L [Ом] и емкостным XC = 1/C [Ом] сопротивлениями,
где: f [с-1] – угловая частота; f [Гц] - частота тока в цепи (f=50 Гц).
Рис.
3
R
X
Z




Z =
 или Z =
или Z =
 .
.
Кроме того, справедливо: R=Z*cos, X= Z*sin = arctg (X/R).



UR
Рис. 4
UX
U
Рис. 5
P
Q
S
Кроме того, соотношения между полной S (мощностью всей цепи), активной P (мощностью на активных элементах цепи) и реактивной Q =QL – QC (мощностью на реактивных элементах цепи), также определяется треугольником (рис .5).
Отметим, что угол = U – I называется углом сдвига фаз и является одним из важнейших параметров цепей переменного синусоидального тока. Он показывает разницу между начальными фазами векторов напряжения – U и тока – I, и одинаков для всех приведенных треугольников. Это свойство цепей переменного тока значительно облегчает их расчет, так как многие параметры цепи могут быть найдены из геометрических соотношений.
Необходимо отметить, что:
вектор напряжения UR совпадает по фазе с вектором тока I. Действующее значение этого напряжения UR = R*I;
вектор напряжения UL опережает по фазе вектор тока I на угол . Действующее значение этого напряжения UL = XL*I;
вектор напряжения UC отстает по фазе от вектора тока I на угол Действующее значение этого напряжения UC = XC*I.
Таким образом, возможны три режима работы цепи переменного синусоидального тока, определяемые соотношением между величинами индуктивного XL и емкостного XC сопротивлений:
XL > XC, тогда UL > UC, и вектор напряжения U опережает по фазе вектор тока I на угол , лежащий в пределах 0 < < Такая цепь (нагрузка) называется активно-индуктивной (рис. 6).
XL < XC, тогда UL < UC, и вектор напряжения U отстает по фазе от вектор тока I на угол , лежащий в пределах -< < 0Такая цепь (нагрузка) называется активно-емкостной (рис. 7).
XL = XC, тогда UL = UC, и вектор напряжения U совпадает по фазе с вектором тока I. Угол 0. Такой режим работы последовательной цепи синусоидального тока называется резонансом напряжений (рис. 8).
U
Рис.
6
UC
UL
I
UR
UK
0
U
Рис.
8
UC
UL
I
UR
UK
U
Рис.
7
UC
UL
I
UR
UK













XL = XC или L = 1/C
следуют условия, с помощью которых можно добиться возникновения резонанса в цепи:
путем подбора частоты рез = 1/
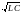 питающего напряжения;
питающего напряжения;
путем подбора индуктивности Lрез = 1/C катушки;
путем подбора емкости Cрез = 1/L конденсатора (в данной работе резонанса добиваются именно этим способом).
Очевидно, что при резонансе напряжений величина реактивного сопротивления Xрез = XL – XC равна нулю, а полное сопротивление цепи Zрез = R. Поэтому, действующее значение резонансного тока (величина которого максимальна) определяется формулой:
 Iрез
= U/Zрез
= U/R
max.
Iрез
= U/Zрез
= U/R
max.
При этом, вектора напряжений UL и UC на реактивных элементах достигают величин UL = Iрез XL и UC = Iрез XC, численно равны между собой, и противоположны по направлению. Следовательно напряжение цепи, при резонансе напряжений, равно напряжению на активном элементе т.е. U = UR (рис. 8). Отметим, что при условии R<<XL(C) (имеющим, как правило, место в цепях содержащих только катушку индуктивности и емкость) напряжение на реактивных элементах будут во много раз превышать напряжение на зажимах цепи, т.е. U<<UL(C).
Полная мощность последовательной цепи синусоидального тока может быть определена по одной из следующих формул:
S
= UI, S
= ZI2,
S =
 ;
;
соответственно активная мощность:
P = UR I, P = RI2, P = UI cos , P = S cos ;
и реактивная мощность:
Q = QL - QC = (UL - UC) I, Q = XI2 = (XL -XC) I2, Q = UI sin , Q = S sin .
Величина cos = P/S называется коэффициентом мощности. Она показывает какую часть от полной мощности S составляет мощность P, выделяемая на активных элементах цепи.
В режиме резонанса напряжений QL = QC, следовательно полная мощность цепи будет равна активной мощности Sрез= P, а cos = cos 0 = 1.
Объект и средства исследования
Объектом исследования служит последовательная цепь, включающая в себя индуктивную катушку с постоянными параметрами R и L, а также батарею конденсаторов, емкость которой меняется при помощи переключателей П2. Емкость батареи равна сумме емкостей параллельно включенных конденсаторов. Элементы исследуемой цепи смонтированы на плате 10 передней панели стенда.
В качестве электроизмерительных приборов применяются многопредельный миллиамперметр типа. Ý-377 и электронный вольтметр (цифровой или стрелочный). Источником .питания исследуемой цепи являются одна из фаз трёхфазного источника.
Порядок проведения эксперимента









(A~N)
С
Рис. 9
А
V
R, L
2. Установить на вольтметре режим измерения переменного напряжения.
3. После проверки цепи преподавателем подать на нее напряжение, установив выключатель В1(3~36 ) в положение "Вкл."
4. Постепенно увеличивая емкость батареи конденсаторов с помощью переключателей П2 (емкость батареи равна сумме емкостей включенных конденсаторов) и замеряя ток цепи, заполнить таблицу 1 протокола испытаний.
5. Установить в цепи режим резонанса напряжений. Для этого необходимо (ориентируясь на данные предыдущего опыта) меняя емкость батареи конденсаторов получить максимально возможное значение тока I. Уточнить значение емкости при которой наступает резонанс, замерив и сравнив между собой напряжения на катушки индуктивности UК и на батареи конденсаторов UС (UК должно быть на 1...5 В больше чем UС). Полученные данные занести в таблицу 2.
6. Согласовать с преподавателем результаты экспериментов, после чего разобрать электрическую цепь.
Обработка результатов эксперимента
По данным таблиц 1 и 2 определить величину XC емкостного сопротивления цепи, считая, что частота f питающего напряжения равна 50 Гц. Результаты вычислений занести в таблицу 3. Привести расчетные формулы.
По данным таблицы 2 определить величину R активного сопротивления катушки. Результаты вычислений занести в таблицу 4. Привести расчетные формулы.
По данным таблицы 2 определить величину XL индуктивного сопротивления катушки. .Результаты вычислений занести в таблицу 4. Привести расчетные формулы.
По данным таблиц 1 и 2 определить величины реактивного X и полного Z сопротивлений цепи, а также угол сдвига фаз . Результаты вычислений занести в таблицу 3. Привести расчетные формулы.
По данным таблицы 2 вычислить величины: напряжения на индуктивности UL, активной P, реактивной Q и полной S мощностей. Результаты вычислений занести в таблицу 4. Привести расчетные формулы.
По данным таблиц 1-4 построить графики зависимостей (рис.11) X = f(C), Z = f(C), = f(C), I = f(C).
Построить векторную (рис.12) диаграмму для режима резонанса напряжений, считая начальную фазу вектора тока I равной нулю.
Контрольные вопросы и задачи
Укажите признаки наступления резонанса напряжений в последовательной цепи при изменении емкости конденсатора.
Какие векторы на векторной диаграмме имеют при резонансе напряжений одинаковую длину?
При каком условии возникает резонанс напряжении и почему?
Изобразите векторную диаграмму тока и напряжений в последовательной цепи при условии XL > XC.
Изобразите векторную диаграмму тока и напряжений в последовательной цепи при условии XL < XC.
Изобразите векторную диаграмму тока и напряжении в последовательной цепи при резонансе напряжении.
Активное сопротивление цепи равно ёмкостному и равно половине индуктивного сопротивления. Чему равен угол сдвига фаз между током и напряжением?
Полная мощность, коэффициент мощности и активное сопротивление цепи соответственно равны: 1 кВА; 0,8 и 2 0м. Чему равно действующее значение тока в цепи?
Полная мощность и реактивное сопротивление цепи соответственно равны 400 ВА и 2 0м. Угол сдвига фаз между током и напряжением равен 30°. Чему равно действующее значение напряжения на зажимах цепи?
Активное и реактивное сопротивления и реактивная мощность цепи соответственно равны 3 Ом, 4 Ом, 36 вар. Чему равна полная мощность цепи?
Полное сопротивление, коэффициент мощности напряжения цепи соответственно равны 10 Ом; 0,6 и 20 В. Чему равна активная мощность цепи?
Сопротивление и мощность конденсатора соответственно равны 10 Ом, 90 вар. Индуктивная составляющая напряжение равна 50 В. Чему равна реактивная мощность цепи?
Активная, индукция и ёмкостная мощность цепи соответственно равны 6 Вт , 10вар и 2 вар. Чему равен коэффициент мощности цепи.
Напряжение, ток и сдвиг фаз между ними соответственно равны 200 В, 10 А, 37 град. Чему равно реактивное сопротивление цепи?
Приложение
ПРОТОКОЛ ИСПЫТАНИЙ






Рис. 10
N
A
U
С
А
R, L
К лабораторной работе ¹5. «Исследование линейной неразветвленной электрической цепи синусоидального тока»
Таблица 1.
C, мкФ. |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
I, А. |
|
|
|
|
|
|
|
|
|
|
Таблица 2.
Cрез, мкФ. |
Iрез, А. |
U, В. |
UК, В |
UС, В |
|
|
|
|
|
РСЧЕТНО–ГРАФИЧЕСКАЯ ЧАСТЬ.
Таблица 3.
C, мкФ. |
|
|
|
|
|
|
|
|
|
|
|
XC, Ом |
|
|
|
|
|
|
|
|
|
|
|
X, Ом |
|
|
|
|
|
|
|
|
|
|
|
Z, Ом |
|
|
|
|
|
|
|
|
|
|
|
, град. |
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.
R, Ом. |
XL, Ом. |
UL, В. |
P, Вт. |
Q, вар. |
S, ВА. |
|
|
|
|
|
|
Расчетные формулы:
C мкФ
0
10 20 30 40 50 60 70
80 90
I A
Z Ом
X Ом
град.
Рис.
11








 Векторная
диаграмма: mI
= А/см., mU
= В/см .
Векторная
диаграмма: mI
= А/см., mU
= В/см .
+j
+1
Рис.
12


Краткие выводы по работе:
Группа _______ Студент ________ «__» _______ 20__ г.
Преподаватель__________________________
Лабораторная работа №5.
Тема: ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ ПРОВОДНИКА.
Время-2 час
Цель: Сформировать знания студентов в измерении удельного сопротивления, опытным путем обучить проводить замеры удельного сопротивления с помощью измерительных приборов.
Введение
Электрический ток есть упорядоченное движение зарядов. Эти заряды в учениях о токах называются носителями тока. В металлах и полупроводниках носителями тока являются электроны, в электролитах и ионизованных газах – положительные и отрицательные ионы.
Одним из главных способов возбуждения электрического тока в телах является создание и поддержание в них электрического поля. Как показывает опыт, для многих тел (например, металлов) в широких пределах плотность электрического тока j пропорциональна напряженности электрического поля Е. Это – один из важнейших, хотя и не фундаментальных, законов электродинамики. Он называется законом Ома (1787-1854). Математически закон Ома выражается формулой:
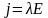 (1)
(1)
где λ - постоянная для данного материала величина, называемая его удельной проводимостью или электропроводностью. Она зависит от физического состояния тела (температуры, давления и пр.).
Строго говоря, закон Ома справедлив лишь для физически однородных тел. Величина, обратная электропроводности, называется удельным сопротивлением материала:
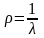 (2)
(2)
Рассмотрим случай, когда электрические токи текут вдоль тонких проводов (проволок). Направление тока будет совпадать с направлением оси провода. Через поперечное сечение S провода в единицу времени проходит количества электричества
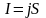 (3)
(3)
называемое силой тока и просто током. Если ток постоянен, то из-за сохранения заряда величина I будет одна и та же вдоль всего провода.
Пусть
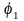 и
и
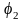 – потенциалы
концов 1 и 2 провода длиной
– потенциалы
концов 1 и 2 провода длиной

 (4)
(4)
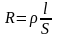 (5)
(5)
Величина, определяемая формулой (5), называется электрическим сопротивлением или просто сопротивлением провода. Формула (4) выражает закон Ома для участка цепи в интегральной форме, в отличие о формулы (1) выражающей этот же закон в дифференциальной форме.
Сопротивление проводника можно измерить двумя способами:
Измерение сопротивления по методу с точным измерением тока (основным измерительным прибором является амперметр).
Измерение сопротивления с точным измерением напряжения.
При измерении по первому методу используется схема №1, по второму схема №2.
 При
работе с данной схемой воспользуемся
следующими формулами:
При
работе с данной схемой воспользуемся
следующими формулами:
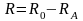
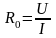
Г де
де
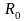 -
общее сопротивление,
-
общее сопротивление,
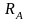 -
внутреннее сопротивление амперметра,
U
– показания вольтметра, I
– показания амперметра.
-
внутреннее сопротивление амперметра,
U
– показания вольтметра, I
– показания амперметра.
Рассмотрим теперь схему 2:
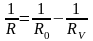
Где
-
общее сопротивление,
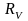 -
внутреннее сопротивление амперметра,
U
– показания вольтметра, I
– показания амперметра.
-
внутреннее сопротивление амперметра,
U
– показания вольтметра, I
– показания амперметра.
Точность расчетов по этим схемам определяется точностью амперметра и вольтметра.
Теперь если мы в качестве сопротивления возьмем проводник длинной , поперечным сечением S, то, зная R, сможем определить удельное сопротивление:
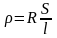 (6)
(6)
Выполнение работы.
Измерение удельного сопротивления по методу с точным измерением тока.
Включить прибор с помощью переключателя «сеть»
Установить режим точного измерения тока
Передвижной кронштейн установить на 0.7 длины резисторного провода по отношению к основанию.
При помощи потенциомера установить такое значение тока, что бы вольтметр показывал
 измерительного диапазона.
измерительного диапазона.Снять показания вольтметра и амперметра.
Определить длину измеряемого провода при помощи шкалы прибора.
Подобные измерения произвести 5-7 раз, данные занести в таблицу 1.
Таблица1
n\n |
|
|
|
|
|
|
|
|
1. 2. . . 7. |
|
|
|
|
|
|
|
|
По формуле
 определить R;
определить R;
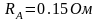 - сопротивление амперметра.
- сопротивление амперметра.
По формуле (6) определить удельное сопротивление исследуемого проводника. Диаметр проводника d=0.36 мм.
Рассчитать погрешность измерений.
Измерение удельного сопротивления по методу с точным определением напряжения.
Включить прибор с помощью переключателя «сеть»
Установить режим точного измерения напряжения.
Согласно пунктам 3-7 первой части провести измерения, данные занести в таблицу 2
Таблица 2
n\n |
|
|
|
|
|
|
|
|
1. 2. . . 7. |
|
|
|
|
|
|
|
|
4.
Пользуясь формулой
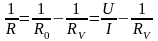 ,
определите R;
=2500
Ом – внутренне сопротивление проводника.
,
определите R;
=2500
Ом – внутренне сопротивление проводника.
5. Рассчитать погрешность измерений.
Контрольные вопросы:
Закон Ома в интегральной и дифференциальной формах.
Сопротивление, удельное сопротивление, зависимость удельного сопротивления от температуры.
Вывод рабочих формул.
Литература:
1.М.В.Немцов,И.И.Светлакова Электротехника-2008г.
2.Л.И.Фуфаева Электротехника-2009г.
3.В.М. Прошин Лабораторно-практические работы по электротехнике-2009г.
Лабораторная работа№6
Тема: Прямые и косвенные методы измерения сопротивления, методы сравнения для измерения сопротивлений.
Время- 4 час
Цель работы: Сформировать знания студентов различными методами измерения сопротивлений и определение сопротивления с помощью мостиковой схемы.
Основные понятия и закономерности
Если в рассматриваемом участке цепи отсутствует источник тока, то сторонние силы не действуют, а участок цепи называется однородным. Для однородного участка цепи выполняется закон, экспериментально установленный немецким физиком Омом в 1826 г. Согласно закону Ома для однородного участка цепи, сила тока прямо пропорциональна падению напряжения на проводнике:
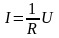 . (6.1)
. (6.1)
В
отсутствие сторонних сил напряжение
 совпадает с разностью потенциалов
,
поддерживаемой на концах проводника.
Величина
совпадает с разностью потенциалов
,
поддерживаемой на концах проводника.
Величина
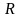 называется электрическим сопротивлением
проводника. Единицей сопротивления в
СИ служит Ом. В соответствии с формулой
(6.1) 1 Ом – это сопротивление такого
проводника, в котором при напряжении
1 В течет ток силой 1 А.
называется электрическим сопротивлением
проводника. Единицей сопротивления в
СИ служит Ом. В соответствии с формулой
(6.1) 1 Ом – это сопротивление такого
проводника, в котором при напряжении
1 В течет ток силой 1 А.
Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для цилиндрического проводника
,
где – длина проводника,
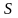 - площадь его
поперечного сечения,
- площадь его
поперечного сечения,
– зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением, измеряется в СИ в Ом×м (омо-метрах).
Величина удельного сопротивления определяется химической природой вещества и условиями, при которых оно находится (в частности, температурой).
Опыт показывает, что для большинства металлов сопротивление растет с температурой приблизительно по линейному закону:
 (6.2)
(6.2)
где
и
- удельное сопротивление и сопротивление
проводника при температуре
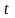 °С,
°С,
 и
- удельное сопротивление и сопротивление
проводника при температуре
и
- удельное сопротивление и сопротивление
проводника при температуре
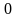 °С,
°С,
 – температурный коэффициент сопротивления,
для чистых металлов (при не очень низких
температурах) близкий к 1/273 К-1.
– температурный коэффициент сопротивления,
для чистых металлов (при не очень низких
температурах) близкий к 1/273 К-1.
Методы измерения сопротивления
Для
определения сопротивлений проводников
существуют различные методы. Одним из
распространенных методов является
измерение сопротивлений с помощью
вольтметра и амперметра. В этом методе
сопротивление проводника определяют
по закону Ома для участка цепи
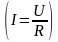 :
:
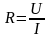 , (6.3)
, (6.3)
где U – разность потенциалов на концах проводника,
I – сила тока в проводнике.
Сила тока измеряется амперметром, который присоединяется последовательно с неизвестным сопротивлением Rx, а разность потенциалов – вольтметром V, включенным параллельно измеряемому сопротивлению (рисунок 6.1).
 Рисунок
6.1 – Схема для определения сопротивления,
если
RV
>> Rx
Рисунок
6.1 – Схема для определения сопротивления,
если
RV
>> Rx
При включении вольтметра в цепь часть тока протекает через вольтметр, и амперметр покажет не ток, протекающий через сопротивление Rx, а сумму токов, протекающих через Rx и вольтметр V, т.е.
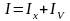 .
.
Вследствие этого в формулу (6.3) следует подставить не Rx, а общее сопротивление параллельно соединенных ветвей между точками 1 и 2: вольтметра RV и сопротивления Rx. Это сопротивление равно:
 . (6.4)
. (6.4)
Из
формулы (10.4) видно, что
 ,
если RV >> Rx
(сопротивление RV
вольтметра должно быть значительно
больше измеряемого сопротивления Rx).
,
если RV >> Rx
(сопротивление RV
вольтметра должно быть значительно
больше измеряемого сопротивления Rx).
Если это условие не выполняется, то неизвестное сопротивление определяется из соотношения (10.4):
 .
.
Так как , то
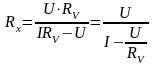 . (6.5)
. (6.5)
Как следует из формулы (6.5), для определения сопротивления Rx кроме тока I и напряжения U необходимо знать также и сопротивление вольтметра RV. На некоторых типах вольтметров это сопротивление указано. На многопредельных вольтметрах указывается максимальный ток Imax, протекающий через прибор при отклонении стрелки на всю шкалу. Эта величина является характерной для данного прибора и не зависит от предела измерений. Сопротивление такого прибора находится как отношение:
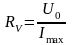 ,
,
где U0 – выбранный предел измерения напряжения. На различных пределах измерения сопротивление RV различно.
Чтобы
исключить влияние вольтметра, амперметр
А можно включить так, как показано на
рисунке 6.2. В этом случае амперметр
измеряет ток, протекающий по неизвестному
сопротивлению Rx,
но тогда вольтметр показывает разность
потенциалов не на Rx,
а сумму разностей потенциалов на Rx
и на амперметре А. В этом случае отношение
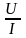 дает не величину Rx,
а общее сопротивление R
между точками 1 и 2 схемы, т.е. R = Rx + RA
(RA
– сопротивление амперметра).
дает не величину Rx,
а общее сопротивление R
между точками 1 и 2 схемы, т.е. R = Rx + RA
(RA
– сопротивление амперметра).
Если RA << Rx, то общее сопротивление . Отношение даёт величину Rx тем точнее, чем сопротивление амперметра RA меньше измеряемого. В общем случае, когда о величине неизвестного сопротивления сказать ничего нельзя, расчет ведется по формуле:
 .
.
 Рисунок
6.2 – Схема для определения сопротивления,
Рисунок
6.2 – Схема для определения сопротивления,
если
сравнима с
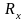 .
.
Отсюда
 . (6.6)
. (6.6)
Обычно на амперметре указано или непосредственно его сопротивление RA или (если прибор многопредельный) величина разности потенциалов Umax между зажимами прибора, соответствующая отклонению стрелки на всю шкалу. В последнем случае сопротивление прибора равно:
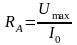 ,
,
где I0 – выбранный предел измерения тока.
На амперметрах с наружными шунтами также бывает указана величина Umax, при делении которой на величину тока, указанного на шунте, получается сопротивление прибора вместе с шунтом.
На практике иногда не учитывают сопротивлений приборов, т.е. отношение принимают за величину неизвестного сопротивления. Систематическая ошибка, которая возникает при этом, зависит от величины измеряемого сопротивления и от сопротивлений применяемых приборов.
Как следует из рассуждений, схемы на рисунках 6.1 и 6.2 неравноценны: при одинаковых приборах схема 6.1 даёт меньшую ошибку при малом неизвестном сопротивлении, схема 6.2 – при большом. Если ошибка незначительна при измерениях токов и разностей потенциалов, то нет надобности учитывать влияние сопротивлений приборов и с достаточной степенью точности можно принять:
 . (6.7)
. (6.7)
Очень точным и весьма часто применяемым в лабораторной практике методом является метод мостика постоянного тока (мост Уитстона.).
Принципиальная
схема мостика приведена на рисунке 6.3.
Измеряемое сопротивление Rx
и три других переменных сопротивления
R0, R1
и R2 соединяются
так, что образуется замкнутый
четырехугольник АВСD. В
одну диагональ четырехугольника включён
гальванометр
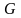 (этот участок и является мостиком), а в
другую через ключ К – источник постоянного
тока e. При замыкании
ключей К и К1 гальванометр показывает
наличие тока Ig
в цепи ДС, но можно подобрать такие
сопротивления R1
и R2, что потенциалы
точек С и Д станут равными, тогда ток в
цепи гальванометра будет отсутствовать
– мост уравновешен (при замыкания ключа
К1 стрелка гальванометра остается
на нуле).
(этот участок и является мостиком), а в
другую через ключ К – источник постоянного
тока e. При замыкании
ключей К и К1 гальванометр показывает
наличие тока Ig
в цепи ДС, но можно подобрать такие
сопротивления R1
и R2, что потенциалы
точек С и Д станут равными, тогда ток в
цепи гальванометра будет отсутствовать
– мост уравновешен (при замыкания ключа
К1 стрелка гальванометра остается
на нуле).
 Рисунок
6.3 – Мост Уитстона
Рисунок
6.3 – Мост Уитстона
В этом случае имеют место следующие соотношения:
 ,
,
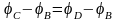 , (6.8)
, (6.8)
т.е.
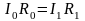 (6.9)
(6.9)
и
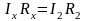 . (6.10)
. (6.10)
Применяя к узлам С и D первое правило Кирхгофа, в случае отсутствия тока через гальванометр будем иметь:
 ,
,
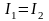 .
.
Деля уравнение (10.9) на уравнение (6.10) и произведя сокращение, получим:
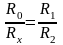 . (6.11)
. (6.11)
Откуда искомое сопротивление Rx равно:
 . (6.12)
. (6.12)
Соотношение (10.12) можно получить, используя правила Кирхгофа:
1.
Первое правило Кирхгофа – алгебраическая
сумма токов, сходящихся в узле, равна
нулю:
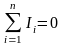 .
Узлом называется точка, в которой
сходится более, чем два проводника.
Направления токов через элементы цепи
выбираются произвольным образом. Ток,
текущий к узлу, считается имеющим один
знак (например, плюс), текущий от узла –
имеющим другой знак (например, минус).
Уравнения первого правила Кирхгофа
можно написать для каждого из N
узлов цепи, но независимыми будет только
N-1 уравнение.
.
Узлом называется точка, в которой
сходится более, чем два проводника.
Направления токов через элементы цепи
выбираются произвольным образом. Ток,
текущий к узлу, считается имеющим один
знак (например, плюс), текущий от узла –
имеющим другой знак (например, минус).
Уравнения первого правила Кирхгофа
можно написать для каждого из N
узлов цепи, но независимыми будет только
N-1 уравнение.
2.
Второе правило Кирхгофа применяется
для замкнутого контура электрической
цепи – алгебраическая сумма произведения
токов на сопротивления соответствующих
участков контура равна алгебраической
сумме ЭДС, встречающихся в контуре:
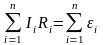 .
Для выбранного контура выбирается
произвольным образом направление обхода
и ток на данном участке считается
положительным, если его направление
совпадает с направлением обхода контура.
ЭДС считается положительной, если при
данном направлении обхода мы переходим
внутри источника тока от отрицательного
полюса источника к положительному.
.
Для выбранного контура выбирается
произвольным образом направление обхода
и ток на данном участке считается
положительным, если его направление
совпадает с направлением обхода контура.
ЭДС считается положительной, если при
данном направлении обхода мы переходим
внутри источника тока от отрицательного
полюса источника к положительному.
Для данной электрической схемы всего должно быть составлено 6 уравнений (число уравнений определяется числом неизвестных токов). По первому правилу Кирхгофа можно составить три уравнения (4 узла) и три уравнения по второму правилу Кирхгофа,
Применим первое правило Кирхгофа к узлам С и D. Будем считать, что при замкнутом ключе К ток через гальванометр Ig направлен от точки С к точке D. Тогда имеем:
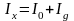 ,
,
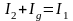 . (6.13)
. (6.13)
По второму правилу Кирхгофа для контуров САDС и ВСDВ (обход против часовой стрелки) получим:
 ,
,
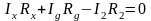 . (6.14)
. (6.14)
При равновесии мостика Уитстона Ig = 0 и соотношения (6.13) и (6.14) примут вид:
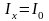 ,
,
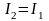 ,
,
, ,
откуда
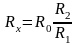 .
.
Метод измерения сопротивлений с помощью моста Уитстона является методом сравнения или нулевым методом, так как в этом случае производится непосредственное сравнение сопротивлений, а гальванометр используется в качестве индикатора отсутствия тока (нуль-гальванометр). Поэтому точность измерения определяется только точностью магазинов сопротивлений и чувствительностью гальванометра.
Порядок выполнения работы и обработка результатов измерения
1. Собрать электрическую цепь, как показано на рисунке 6.3. Вместо сопротивления Rx включить в цепь одну из катушек с неизвестным сопротивлением Rx1, а в качестве источника постоянного тока использовать выпрямитель.
2. По указанию преподавателя выставить значения сопротивлений R1 и R2.
3. Изменяя сопротивление магазина R0, добиться отсутствия тока в цепи гальванометра.
4. Вычислить неизвестное сопротивление Rx1 по формуле (6.12).
5. Те же измерения произвести с другой катушкой, определить её сопротивление Rx2.
6. Включить обе катушки в цепь сначала последовательно, а затем параллельно, и измерить указанным методом сопротивления при последовательном Rпосл,эксп. и параллельном Rпарал,эксп. соединении.
Все полученные на опыте и вычисленные результаты занести в таблицу 10.1.
Таблица 10.1
Измеряемое сопротивление |
R0, Ом |
R1, Ом |
R2, Ом |
Rx, Ом |
DR, Ом |
|
Катушка № 1 |
|
|
|
|
|
|
Катушка № 2 |
|
|
|
|
|
|
Катушки № 1 и № 2 включены последовательно |
|
|
|
|
|
|
Катушки № 1 и № 2 включены параллельно |
|
|
|
|
|
|
7. Пользуясь полученными в п.п. 1 ¸ 5 значениями сопротивлений катушек №1 и №2 по формулам для последовательного и параллельного проводников вычислить теоретические значения сопротивлений Rпосл,теор. и Rпарал,теор.
8.
Вывести формулы для относительных и
абсолютных погрешностей величин Rx1,
Rx2,
Rпосл,эксп.,
Rпарал,эксп.,
Rпосл,теор.,
Rпарал,теор.
Вычислить эти погрешности. Относительная
погрешность магазина сопротивлений
Р33 (в процентах) вычисляется по формуле
 .
Здесь Rmax
– наибольшее значение сопротивления,
которое можно выставить на магазине,
Ом; R0 –
номинальное значение включенного
сопротивления,
.
Здесь Rmax
– наибольшее значение сопротивления,
которое можно выставить на магазине,
Ом; R0 –
номинальное значение включенного
сопротивления,
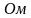 .
.
9. Сравнить с учётом погрешности определённые экспериментально и теоретически рассчитанные значения сопротивления при последовательном и параллельном соединении катушек.
10. По данным о диаметре и длине проволоки, из которой намотаны катушки, рассчитать удельное сопротивление материала проволоки. По табличным данным определить металл, из которого изготовлена проволока.
Контрольные вопросы:
Что такое сила тока, напряжение?
Закон Ома для однородного, неоднородного участков и для полной цепи.
Правила Кирхгофа.
Измерение сопротивления с помощью амперметра и вольтметра. Недостатки этого метода измерений.
Вывести условие равновесия мостика Уитстона.
Каковы преимущества мостиковой схемы?
От чего зависит точность измерения сопротивлений при помощи мостиковой схемы?
Сопротивление проводника. Его физический смысл. От чего зависит сопротивление проволоки?
Удельное сопротивление проводника. Единицы измерения.
Параллельное и последовательное соединение проводников.
Во сколько раз изменится сопротивление участка цепи, если N одинаковых проводников, соединенных последовательно, соединить параллельно?
Лабораторная работа№7 Тема "исследование трехфазной четырепроводной электрической цепи синусоидального тока
Время-2 час
Цель: Сформировать знания студентов об исследовании трехфазной четырехпроводной электрической цепи синусоидального тока и уметь собирать схемы соединения «звездой» и рассчитывать симметричную и несимметричную нагрузки.
ПОРЯДОК РАБОТЫ:
1. Ознакомиться с приборами, необходимыми для выполнения работы, записать их технические характеристики.
Собрать электрическую цепь (рис.1).

3.
Установить симметричную нагрузку в
фазах и записать показания приборов
при наличии нейтрального провода и без
него. Убедиться, что Uл = Uф /![]()
4. Установить несимметричную нагрузку фаз (разное количество ламп в каждой фазе) и записать показания приборов при наличии нейтрального провода и без него.
5. Установить симметричную нагрузку и, отключив все лампы в одной из фаз потребителя, что соответствует обрыву в данной фазе, записать показания приборов при наличии нейтрального провода и без него.
Установив симметричную нагрузку фаз, отключить нейтральный провод и записать показания приборов при коротком замыкании одной из фаз потребителя (для этого можно проводником замкнуть накоротко зажимы любой фазы). Все данные измерений и вычислений внести в таблицу 1 и построить по этим данным векторные диаграммы для каждого пункта.
Таблица 1.
Характер нагрузки |
UA |
UB |
UC |
UAB |
UBC |
UCA |
IA |
IB |
IC |
IN |
UN |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Симметричная без нейтрального провода |
|
|
|
|
|
|
|
|
|
|
|
Симметричная с нейтральным проводом |
|
|
|
|
|
|
|
|
|
|
|
Несимметричная без нейтрального провода |
|
|
|
|
|
|
|
|
|
|
|
Несимметричная с нейтральным проводом |
|
|
|
|
|
|
|
|
|
|
|
Полная разгрузка одной фазы без нейтрального провода |
|
|
|
|
|
|
|
|
|
|
|
Полная разгрузка одной фазы с нейтральным проводом |
|
|
|
|
|
|
|
|
|
|
|
Короткое замыкание фазы без нейтрального провода |
|
|
|
|
|
|
|
|
|
|
|
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Трехфазной системой переменных токов называется совокупность трех однофазных электрических цепей, в которых действуют три синусоидальные ЭДС одинаковой частоты, сдвинутые по фазе на 1/3 периода и создаваемые одним источником электрической энергии. Обмотки фаз генератора имеют одинаковое число витков и выполняются из провода одинакового сечения, поэтому ЭДС, индуктированные в этих обмотках, равны по величине.
Если каждая из трех фаз генератора работает на отдельную нагрузку, то в этом случае имеет место несвязанная трехфазная система, в которой генератор соединен с нагрузкой 6-ю проводами (рис.2).

Такие системы неэкономичны и практического применения не имеют.
Соединение фаз генератора и нагрузки может осуществляться по схемам "звезда" и "треугольник". Если концы фаз генератора соединить в одну точку, а к началам подвести линейные провода, соединяющих генератор с нагрузкой, то такое соединение называется "звездой" и условно обозначается знаком " " (рис.3).

Чтобы соединить фазы нагрузки по схеме "звезда", следует все концы фаз этого потребителя соединить в одну точку, а начала фаз линейными проводами соединить с источником энергии.
Точки соединения концов фаз генератора (0) и нагрузки (0`) называются соответственно нулевыми, или нейтральными точками генератора и нагрузки.
Обе эти точки соединяются проводом, называемым нулевым или нейтральным.
Таким образом, генератор соединен с нагрузкой четырьмя проводами, поэтому такая система называется трехфазной четырехпроводной.
Токи, протекающие в фазах генератора или нагрузки, называются фазными и обозначаются: IА; IВ; IС или в общем виде IФ.
Токи, протекающие по линейным проводам, называются линейными IЛ.
При соединении "звездой" фаза генератора, линейный провод и фаза нагрузки соединены последовательно, поэтому IЛ = IФ.
По нейтральному проводу протекает ток, равный геометрической сумме трех токов: IО= IА+IВ+IС или алгебраической сумме комплексов этих токов: IО=IА+IВ +IС.
Напряжения, измеренные между началом и концом каждой фазы, называются фазными и обозначаются: UА; UВ; UС или в общем виде UФ. Напряжения UАВ; UВС; UСА называются линейными и измеряются между линейными проводами, т.е. между началами фаз. В линейных проводах принято считать положительными направления токов от генератора к нагрузке, а в нейтральном - от нагрузки к генератору.
Благодаря наличию нейтрального провода, фазные напряжения потребителя остаются неизменными как при симметричной, так и при несимметричной нагрузке.
Если ток в нейтральном проводе равен нулю, что может иметь место при симметричной нагрузке, то трехфазная система может стать трехпроводной (рис.4).

Соотношения между линейными и фазными напряжениями устанавливаются на основании второго закона Кирхгофа. При этом уравнения для действующих значений записываются в векторной (1) или комплексной (2) форме:
UАВ= UА - UВ UАВ = UА - UВ
UВС= UВ - UС (1) UВС = UВ - UС (2)
UСА = UС - UА UСА= UС - UА
Векторные диаграммы, построенные по уравнениям (1), изображены на рис.5

а). б).
Векторная диаграмма рис.5 (а) называется топографической (каждая точка этой диаграммы соответствует точке на схеме).
Из векторной диаграммы рис.5 (б) видно, что "звезда" фазных напряжений отстает от "звезды" линейных напряжений на угол 30. Соотношение между величинами фазных и линейных напряжений для симметричной нагрузки можно вывести, рассматривая один из треугольников, составленных векторами фазных и линейных напряжений.
Например:
![]()
Откуда
![]()
Т.е., линейное напряжение в случае симметричной нагрузки и при наличии нейтрального провода в раз больше фазного.
UО - напряжение, измеряемое между нейтральными точками генератора и потребителя.
СЛУЧАЙ СИММЕТРИЧНОЙ НАГРУЗКИ.
Нагрузка, подключенная к трехфазному генератору, может быть симметричной и несимметричной.
Симметричной называется такая нагрузка, при которой сопротивления фаз одинаковы по величине и по характеру, т.е.
ZА = ZВ = ZС = r + jx
При симметричной нагрузке токи в фазах по величине равны между собой.
IА = IВ = IС,
где
![]()
На Рис.6 показаны векторные диаграммы напряжений и токов для симметричной активной нагрузки (а) - при наличии нейтрального провода
(IА + IВ + IС = IО = 0), а (б) - без нейтрального провода.

Рис.6
СЛУЧАЙ НЕСИММЕТРИЧНОЙ НАГРУЗКИ.
При несимметричной нагрузке ZАZВZС, токи в фазах IАIВIС.
Векторные диаграммы для данного случая изображены на рис.7 (а, б).
На рис.7 (а) показано графическое определение тока в нейтральном проводе IО. Благодаря наличию нейтрального провода при несимметричной нагрузке напряжения на фазах потребителя энергии остаются неизменными и равными фазным напряжениям генератора (если пренебречь сопротивлением нейтрального провода и линейных проводов).

Рис.7
В случае обрыва нейтрального провода нулевая точка смещается в сторону более нагруженной фазы, и напряжения на фазах потребителя изменяются, что приводит к нарушению нормальной работы приемников энергии, поэтому в нейтральный провод не рекомендуется ставить предохранитель или рубильник. Токи в трехфазной цепи без нейтрального провода принимают такие значения, что их геометрическая сумма равна нулю.
Если в качестве нагрузки трехфазной трехпроводной цепи используются лампы накаливания одинаковой мощности, то их накал определяется фазным напряжением, а так как напряжения на фазах различны, то лампы будут гореть с различной яркостью. Наибольший накал ламп будет в той фазе, в которой включено меньшее количество ламп.
В случае обрыва одной из фаз, например, фазы "А" без нейтрального провода (отключены все лампы в этой фазе), две другие фазы ("В" и "С") оказываются включенными последовательно и находятся под линейным напряжением UВС. Если сопротивления одинаковы, то напряжения их будут равны, и каждое составляет половину линейного напряжения UВС/2 (рис.8).

Рис.8
В этом случае лампы, включенные в фазу "А", погаснут, а в фазах "В" и "С" будут иметь меньший накал.
Уменьшение сопротивления одной из фаз (например, "А") до нуля, что соответствует короткому замыканию в ней, приводит к смещению нулевой точки в вершину треугольника линейных напряжений, тогда UА=0, а фазные напряжения UВ и UС становятся равными линейным: UАВ и UСА.
Векторная диаграмма токов и напряжений для данного случая показана на рис.9.

Рис.9
Лампы, включенные в фазу "А", гаснут, а в фазах "В" и "С" горят ярче обычного.
Вывод: при несимметричной нагрузке фаз нельзя применять соединение приемников по схеме "звезда" без нулевого провода.
Содержание отчета
1. Технические характеристики приборов и элементов, используемых в работе.
2. Схемы и таблицы.
3. Расчетные формулы и векторные диаграммы.
4. Выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое соединение фаз генератора и нагрузки называется "звездой"?
2. Каково соотношение между фазными и линейными напряжениями и токами при соединении нагрузки "звездой"?
3. Объяснить назначение нулевого провода.
4. Как определить ток в нулевом проводе?
5. Что такое напряжение смещения нейтрали? в каких случаях оно равно нулю?
6.Чем опасно короткое замыкание одной фазы при наличии и отсутствии нулевого провода?
Лабораторная работа №8.
Тема: Исследование трехфазной цепи при
соединении потребителей «треугольником».
Время:2 час
Цель: Сформировать знания студентов об исследовании трехфазной электрической цепи синусоидального тока и уметь собирать схемы соединения « треугольником» и рассчитывать симметричную нагрузку.
Собрать схему рисунка 6-1.
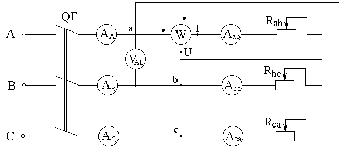
Рисунок 6-1 – Схема трехфазной цепи при соединений нагрузки треугольником
На схеме: QF – автоматический выключатель трёхфазный; VАВ – вольтметр со шкалой до 150В; АA, АB, АC, Аab, Аbc, Аca – амперметры со шкалой до 2,5А; W – ваттметр.
Подключить цепь к трехфазному источнику (линейное напряжение не выше 90В).
Установить несимметричную активную нагрузку (изменяя реостатами фазные сопротивления установить по приборам различные значения фазных токов, не превышающие допустимые значения для реостатов). Результаты измерений внести в таблицу 6-1 (пункт 1).
4. Установить симметричную активную нагрузку (фазные токи не выше 1,5А). Результаты измерений внести в таблицу 6-1 (пункт 2).
5. Выключить QF и сделать разрыв в линейном проводе фазы “А” (в точке “А”). Результаты измерений внести в таблицу 6-1 (пункт 3).
6. Выключить QF и восстановить схему. Сделать разрыв в фазе “аb” (разорвать цепь сопротивления Rab ). Результаты измерений внести в таблицу 6-1 (пункт 4).
7. Выключить QF и восстановить схему. Параллельно реостату Rab в фазе “аb” включить конденсатор ёмкостью 30 – 40 мкФ. Результаты измерений внести в таблицу 6-1 (пункт 5).
8. Выключить QF и отключить в фазе “аb” сопротивление Rab, оставив только конденсатор ёмкостью 30 – 40 мкФ. Результаты измерений внести в таблицу 6-1 (пункт 6).
По результатам измерений для всех режимов (пункты 1–6 таблицы 6-1) построить в масштабе векторные диаграммы напряжений и токов (фазных и линейных).
10. Для симметричной активной нагрузки (пункт 2 таблицы 6-1) определить соотношение между линейными и фазными токами.
Таблица 6-1 – Результаты измерений в трехфазной цепи
при различных режимах работы
№ |
Режим цепи |
IA, А |
IB, А |
IC, А |
Iаb, А |
Ibс, А |
Iса, А |
UAB, B |
Pab, Вт |
1 |
Несимметричная активная нагрузка |
|
|
|
|
|
|
|
|
2 |
Симметричная активная нагрузка |
|
|
|
|
|
|
|
|
3 |
Разрыв в линейном проводе фазы “A” |
|
|
|
|
|
|
|
|
4 |
Разрыв в фазном проводе “ab” |
|
|
|
|
|
|
|
|
5 |
Реостат в фазе “аb” соединен параллельно с конденсатором |
|
|
|
|
|
|
|
|
6 |
В фазе “аb” включен конденсатор |
|
|
|
|
|
|
|
|
Контрольные вопросы:
1. Как образуется соединение треугольником?
2. Какая нагрузка называется симметричной?
3. Какой режим работы называется симметричным?
4. Какой ток называется линейным?
5. Какой ток называется фазным?
6. Какое соотношение существует между линейными и фазными токами при симметричной нагрузке?
7. Как связаны между собой линейные и фазные токи при несимметричной нагрузке?
8. Допустимо ли короткое замыкание в цепи, соединенной треугольником?
9. Какое соотношение между линейными и фазными напряжениями при соединении треугольником?
10. Окажет ли влияние обрыв одной фазы нагрузки на режим работы двух оставшихся фаз?
11. Объяснить построение векторных диаграмм напряжений и токов для симметричной нагрузки.
12. Объяснить построение векторных диаграмм напряжений и токов для несимметричной нагрузки.
13. Объяснить построение векторных диаграмм напряжений и токов при обрыве линейного провода.
14. Объяснить построение векторных диаграмм напряжений и токов при обрыве фазного провода.
15. Почему показание ваттметра равно нулю при выполнении пункта
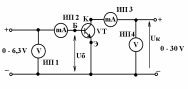
Лабораторная работа 9
Тема: Исследование цепи трехфазной цепи при
соединении потребителей «звездой».
Время-2 час
Цель: Сформировать знания студентов об исследовании трехфазной электрической цепи синусоидального тока и уметь собирать схемы соединения «звездой» и рассчитывать симметричную нагрузку.
1. Собрать схему рисунка 5-1.
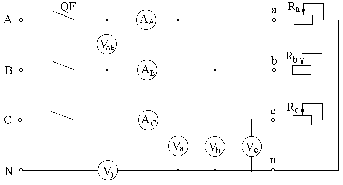
Рисунок 5-1 – Схема трехфазной цепи при соединении нагрузки звездой
На схеме: QF – автоматический выключатель трёхфазный; VАВ, Va, Vb , Vс – вольтметры со шкалой до 150В; Vo – вольтметр со шкалой до 60B (75В); АA , АB , АC – амперметры со шкалой до 2,5А.
Подключить цепь к трехфазному источнику (линейное напряжение не выше 90В).
Закоротить вольтметр Vo (схема с нейтральным проводом) и установить симметричную активную нагрузку (по равенству показаний амперметров). Результаты измерений внести в таблицу 5-1 (пункт 1).
4. При симметричной активной нагрузке восстановить схему (включить вольтметр Vo – схема без нейтрального провода). Результаты измерений внести в таблицу 5-1 (пункт 2).
5. Сделать разрыв в фазном проводе фазы “A” (в точке "а" схемы). Результаты измерений внести в таблицу 5-1 (пункт 3).
6. Восстановить схему электрической цепи. Реостатом Ra изменить величину сопротивления в фазе “A”. Зафиксировать показания приборов для двух значений сопротивления – пункты 4,5 таблицы 5-1.
7. Вывести сопротивление реостата в фазе “A” до нуля (короткое замыкание). Результаты измерений внести в таблицу 5-1 (пункт 6).
8. Заменить реостат в фазе “A” Rа катушкой индуктивности (вариометром). Результаты измерений внести в таблицу 5-1 (пункт 7).
9. Заменить вариометр в фазе “A” конденсатором ёмкостью 30 - 40 мкФ. Результаты измерений внести в таблицу 5-1 (пункт 8).
10. Закоротить вольтметр Vo (схема с нейтральным проводом) при включенном в фазу “A” конденсаторе емкостью 30 - 40 мкФ. Результаты измерений внести в таблицу 5-1 (пункт 9).
Применяя метод засечек, построить для всех режимов трёхфазной цепи (пункты 1 – 9 таблицы 5-1) в масштабе топографические диаграммы фазных напряжений источника и приёмника, а также векторные диаграммы токов. Для режима с нейтральным проводом (пункт 9) графически определить значение тока в нейтральном проводе.
Определить соотношение между линейными и фазными напряжениями для симметричной нагрузки (пункты 1,2).
Таблица 5-1 – Результаты измерений в трехфазной цепи
при различных режимах работы
№ |
Режим цепи |
IA, А |
IB, А |
IC, А |
Vа, В |
Vb, В |
Vc, В |
V0, В |
VAB, В |
||
1 |
Сим- метричная нагрузка |
С нейтральным проводом |
Активная |
|
|
|
|
|
|
|
|
2 |
Без нейтрального провода |
Активная |
|
|
|
|
|
|
|
|
|
3 |
Несимметричная нагрузка |
Без нейтрального провода |
Ra = |
|
|
|
|
|
|
|
|
4 |
Ra = Rа1 |
|
|
|
|
|
|
|
|
||
5 |
Ra = Rа2 |
|
|
|
|
|
|
|
|
||
6 |
Ra = 0 |
|
|
|
|
|
|
|
|
||
7 |
Вариометр в фазе “A” |
|
|
|
|
|
|
|
|
||
8 |
Конденсатор в фазе “A” |
|
|
|
|
|
|
|
|
||
9 |
С нейтральным проводом |
Конденсатор в фазе “A” |
|
|
|
|
|
|
|
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как образуется соединение звездой?
2. Какая нагрузка называется симметричной?
3. Какой режим pаботы трехфазной цепи называется симметричным?
4. Какое напряжение называется линейным?
5. Какое напряжение называется фазным?
6. Какова роль нейтрального провода?
7. Влияет ли нейтральный провод на режим работы трехфазной цепи при симметричной нагрузке?
8. Оказывает ли влияние сопротивление в нейтральном проводе на режим работы трехфазной цепи при симметричной нагрузке?
9. Оказывает ли влияние сопротивление в нейтральном проводе на режим работы в трехфазной цепи при несимметричной нагрузке?
10. Какое напряжение называется напряжением смещения нейтрали?
11. Чему равно напряжение смешения нейтрали при обрыве фазы?
12. Чему равно напряжение смещения нейтрали при коротком замыкании фазы?
13. Объяснить построение топографической диаграммы напряжений и векторной диаграммы токов при обрыве фазы.
14. Почему при коротком замыкании фазы в трехфазной цепи напряжения на фазах нагрузки равны линейным напряжениям?
15. Объяснить построение топографической диаграммы напряжений и векторной диаграммы токов при коротком замыкании в фазе “А”.
16. Допустимо ли короткое замыкание фазы при отсутствии нейтрального провода?
17. Допустимо ли короткое замыкание фазы при наличии нейтрального провода?
18. Объяснить построение топографической диаграммы напряжений и векторной диаграммы токов при включении в фазу “А” вариометра при отсутствии нейтрального провода.
19. Объяснить построение топографической диаграммы напряжений и векторной диаграммы токов при включении в фазу “А” вариометра при наличии нейтрального провода.
20. Объяснять построение топографической диаграммы напряжений и векторной диаграммы токов при включении в фазу “А” конденсатора при отсутствии нейтрального провода.
21.Объяснять построение топографической диаграммы напряжений и векторной диаграммы токов при включении в фазу “А” конденсатора при наличии нейтрального провода.
ЛАБОРАТОРНАЯ РАБОТА №10
Тема: Испытание однофазного трансформатора Время-4 час
Цель работы:
Произвести испытание однофазного трансформатора в режимах холостого хода, короткого замыкания и в режиме нагрузки резистивными приемниками.
Экспериментально определить коэффициент трансформации, ток холостого хода, потери мощности в сердечнике.
Экспериментально определить напряжение короткого замыкания и потери мощности в обмотках при номинальной нагрузке.
По экспериментальным данным построить внешнюю характеристику трансформатора и определить изменение напряжения при нагрузке.
По экспериментальным данным построить рабочие характеристики трансформатора.
Содержание
Трансформатор - статический электромагнитный аппарат, в котором посредством магнитного поля, переменный ток одного напряжения преобразуется в переменный ток другого напряжения той же частоты. |
Рис. 1. Электромагнитная
схема
трансформатора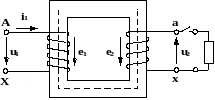
|
(1) |
|
(2) |
Если вторичная обмотка замкнута, то под действием ЭДС ”е2” в цепи вторичной обмотки потечет ток. Отношение электродвижущих сил определяется отношением чисел витков первичной и вторичной обмоток и для трансформатора есть постоянная величина, которая называется коэффициентом трансформации.
|
(3) |
Величина коэффициента трансформации может быть найдена экспериментально или вычислена по паспортным данным.
В паспорт трансформатора заносятся номинальная мощность S, номинальное напряжение и токи обмоток. Номинальной полезной мощностью трансформатора называется полная мощность на зажимах вторичной обмотки - S2н, она приблизительно равна полной мощности потребляемой первичной обмоткой - S1н, т.е.
|
(4) |
Номинальным напряжением называется напряжение на зажимах обмотки при холостом ходе трансформатора, обозначается - U1н, U2н.
Номинальным током называется ток, связанный с номинальной мощностью и номинальным напряжением следующим соотношением:
|
(5) |
Эксплуатационные характеристики трансформатора определяются изменением вторичного напряжения при нагрузке, потерями мощности в сердечнике и обмотках, коэффициентом полезного действия. Все эти величины могут быть рассчитаны по данным опытов холостого хода и короткого замыкания, которые характеризуют работу трансформатора в предельных режимах нагрузки: при ее отсутствии I2 = 0 и номинальной - I2 = I2н. Основным режимом работы трансформатора является режим нагрузки, когда вторичная обмотка замкнута на приемник и по ней протекает ток i2. Сила тока i2 определяется величинами ЭДС е2 и полного сопротивления вторичной цепи. При наиболее распространенной индуктивной нагрузке, ток вторичной обмотки отстает от ЭДС - е2 по фазе, при емкостной - опережает ЭДС на некоторый угол, определяемый параметрами вторичной цепи.
Появление тока во вторичной обмотке сопровождается появлением намагничивающей силы - , которая создает в сердечнике магнитный поток, направленный, в соответствии с принципом Ленца, навстречу потоку первичной обмотки, т.е. магнитный поток вторичной обмотки стремится размагнитить магнитопровод. Увеличение вторичного тока приводит к возрастанию мощности вторичной цепи - i2е2.
Согласно закону сохранения энергии это вызывает рост мощности потребляемой первичной обмоткой из сети - i1uи, следовательно,
при неизменной величине первичного напряжения увеличение тока вторичной обмотки приводит к возрастанию тока первичной обмотки. |
Одновременно с увеличением тока первичной обмотки возрастает и намагничивающая сила - i1прирост которой, компенсирует размагничивающее действие вторичного тока.
Магнитный поток в сердечнике трансформатора при нагрузках от 0 до номинальной остается неизменным. |
Протекание тока во вторичной обмотке трансформатора вызывает падение напряжения в ее активном и индуктивном сопротивлениях. Поэтому ЭДС - е2 несколько отличается от напряжения U2 на зажимах вторичной обмотки.
Отклонение величины вторичного напряжения трансформатора от напряжения холостого хода, выраженное в процентах, называется изменением напряжения трансформатора при нагрузке. |
|
(6) |
Эта величина может быть рассчитана по данным опытов холостого хода и короткого замыкания или определена по внешней характеристике, которая представляет собой зависимость вторичного напряжения от коэффициента загрузки - U2 = f(). При индуктивной нагрузке вторичное напряжение уменьшается с ростом вторичного тока. При номинальной нагрузке уменьшение напряжения будет тем больше, чем больше полные сопротивления обмоток.
Величина изменения напряжения при нагрузке зависит также от характера нагрузки. У силовых трансформаторов при изменение напряжения составляет 5-10 %. Чтобы устранить нежелательное уменьшение напряжения на приемниках, трансформатор проектируют так, чтобы напряжение холостого хода U20 было на 5% больше номинального напряжения приемников, кроме того предусматривается возможность изменения числа витков одной из обмоток при возрастании нагрузки.
Порядок выполнения работы
Внимательно прочитайте раздел ”Техника безопасности при работе трансформатора”.
Паспортные данные трансформатора занесите в рабочий журнал.
Таблица 1
Паспортные данные трансформатора ОСМ-О16У3
Тип трансформатора |
U1H |
U2H |
I1H |
I2H |
SH |
|
B |
B |
A |
A |
кВА |
ОСМ-О16У3 |
220 |
110 |
0,727 |
1,54 |
0,160 |
Технические данные электроизмерительных приборов, используемых в работе, занесите в таблицу 2.
Таблица 2
|
Система измерения |
Класс точности прибора |
Диапазон измерения прибора |
|
|
|
|
|
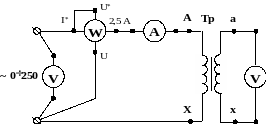
Рис. 2. Схема проведения опыта холостого хода
Соберите схему, изображенную на рисунке 2. Клеммы, маркированные ”I*; 2,5; U*; U”, находятся на ваттметре.
Диапазон измерения вольтметра, включенного в цепь первичной обмотки, установите 0-300 В, диапазон измерения вольтметра, включенного в цепь вторичной обмотки, установите 0-150 В.
Диапазон измерения амперметра установите 0-1 А. Диапазон измерения ваттметра установите 0-75 Вт.
Предъявите цепь для проверки преподавателю или лаборанту.
Автоматическим выключателем ”АП”, расположенным на панели источников питания подайте напряжение на стенд. При этом на панели блока питания должна загореться сигнальная лампа.
Магнитным пускателем, кнопки которого расположены на панели источников питания под клеммами 0~250, подайте напряжение на панель схему. При этом на панели блока питания должна загореться сигнальная лампа.
Регулятором напряжения ”ЛАТР”, расположенным на панели блока питания, установите на первичной обмотке трансформатора номинальное напряжение.
Показания приборов занесите в таблицу 3.
Таблица 3
Результаты испытания трансформатора ОСМ-О16У3 на холостом ходу
Измерено |
Вычислено |
|||||||||
U10, B |
U20, B |
I10, A |
P0, Вт |
i0 |
k12 |
cos |
z12, Ом |
R12, Ом |
x12, Ом |
|
|
|
|
|
|
|
|
|
|
|
|
Регулятором напряжения ”ЛАТР”, расположенным на панели блока питания, снимите напряжение с первичной обмотки трансформатора.
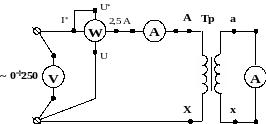
Рис. 3. Схема проведения опыта короткого замыкания
Автоматическим выключателем ”АП”, расположенным на панели блока питания, отключите стенд от сети, при этом на панели блока питания сигнальные лампы должны погаснуть.Соберите цепь, изображенную на рисунке 3.
Диапазон измерения вольтметра, включенного в цепь первичной обмотки, установите 0-75 В.
Диапазон измерения амперметра, включенного в цепь вторичной обмотки, установите 0-2,5 А.
Внимательно прочитайте условия проведения опыта короткого замыкания.
ДЛЯ ПРОВЕДЕНИЯ ОПЫТА КОРОТКОГО ЗАМЫКАНИЯ ПЕРВИЧНОЕ НАПРЯЖЕНИЕ УСТАНОВИТЕ ТАКИМ, ЧТОБЫ В ЦЕПИ ПЕРВИЧНОЙ ОБМОТКИ ПРОТЕКАЛ НОМИНАЛЬНЫЙ ТОК. |
Ручку регулятора напряжения ”ЛАТР”, расположенного на панели блока питания стенда, установите в крайнее положение, по направлению противоположному движению часовой стрелки.
Предъявите цепь для проверки преподавателю или лаборанту.
Автоматическим выключателем ”АП”, расположенным на панели источников питания подайте напряжение на стенд. При этом на панели блока питания должна загореться сигнальная лампа.
Магнитным пускателем, кнопки которого расположены на панели источников питания под клеммами 0~250, подайте напряжение на панель схему. При этом на панели блока питания должна загореться сигнальная лампа.
Регулятором напряжения ”ЛАТР”, расположенным на панели блока питания, установите номинальный ток на первичной обмотке трансформатора.
Показания приборов занесите в таблицу 4.
Таблица 4
Результаты испытания трансформатора ОСМ-О16У3 в режиме короткого замыкания
Измерено |
Вычислено |
||||||||
U1К, В |
I1Н, А |
PК, Вт |
I2Н, А |
uК |
zК, Ом |
RК, Ом |
xК, Ом |
cos К |
|
|
|
|
|
|
|
|
|
|
|
Регулятором напряжения ”ЛАТР”, расположенным на панели блока питания, снимите напряжение с первичной обмотки трансформатора.
Автоматическим выключателем ”АП”, расположенным на панели блока питания, отключите стенд от сети, при этом на панели блока питания сигнальные лампы должны погаснуть.
Соберите цепь, изображенную на рисунке 4.
Диапазон измерения вольтметра, включенного в цепь первичной обмотки, установите 0-300 В. Диапазон измерения ваттметра установите 0-375 Вт.
Предъявите цепь для проверки преподавателю или лаборанту.
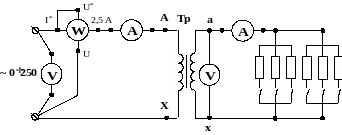
Рис. 4. Схема испытания трансформатора под нагрузкой
Автоматическим выключателем ”АП”, расположенным на панели источников питания подайте напряжение на стенд. При этом на панели блока питания должна загореться сигнальная лампа.Магнитным пускателем, кнопки которого расположены на панели источников питания под клеммами 0~250, подайте напряжение на панель схему. При этом на панели блока питания должна загореться сигнальная лампа.
Регулятором напряжения ”ЛАТР”, расположенным на панели блока питания, установите на первичной обмотке трансформатора номинальное напряжение.
Снимите показания приборов для 4-7 значений вторичного тока. Величину тока изменяйте постепенным увеличением количества включенных резисторов.
СЛЕДИТЕ ЗА ВЕЛИЧИНОЙ ТОКА В ОБМОТКАХ. ВЕЛИЧИНЫ ТОКОВ I1 И I2 НЕ ДОЛЖНЫ ПРЕВЫШАТЬ НОМИНАЛЬНЫХ ЗНАЧЕНИЙ. |
33. Показания приборов занесите в таблицу 5.
Таблица 5
Результаты испытания трансформатора ОСМ-О16У3 под нагрузкой
Измерено |
Вычислено |
||||||||
U1, B |
I1, A |
P1, Вт |
U2, B |
I2, A |
|
P2, Вт |
|
cos |
|
|
|
|
|
|
|
|
|
|
|
Регулятором напряжения ”ЛАТР”, расположенным на панели блока питания, снимите напряжение с первичной обмотки трансформатора.
Автоматическим выключателем ”АП”, расположенным на панели блока питания, снимите напряжение со стенда.
Предъявите результаты экспериментов преподавателю.
По указанию преподавателя на ПЭВМ Агат-9 рассчитайте внешние характеристики и КПД трансформатора при индуктивной и емкостной нагрузках.
Рекомендации по обработке экспериментальных данных
1. Опыт холостого хода.
Рис. 5. Схема
замещения трансформатора на холостом
ходу
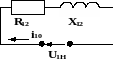
 ,
тогда отношение электродвижущих сил в
формуле (3) можно заменить отношением
напряжений. Схема замещения трансформатора
на холостом ходу (рис. 5) содержит только
элементы намагничивающей цепи R12
и x12. Для нее известны измеренное
экспериментально напряжение U10,
мощность P0 и ток холостого хода
I10.
,
тогда отношение электродвижущих сил в
формуле (3) можно заменить отношением
напряжений. Схема замещения трансформатора
на холостом ходу (рис. 5) содержит только
элементы намагничивающей цепи R12
и x12. Для нее известны измеренное
экспериментально напряжение U10,
мощность P0 и ток холостого хода
I10.
Эти данные легко позволяют, пользуясь законами Ома, Джоуля-Ленца и треугольником сопротивлений, определить сопротивления намагничивающей цепи: полное - z12, активное - R12, реактивное - х12 и коэффициент мощности, также как это делали при выполнении работы ”Последовательная цепь переменного тока”.
i0 - ток холостого хода, выраженный в процентах от номинального - эта величина заносится в паспорт трансформатора.
2. Опыт короткого замыкания.
Рис. 6. Схема
замещения трансформатора при коротком
замыкании

Схема замещения трансформатора (рис. 6) будет содержать только элементы, учитывающие потери в обмотках (RК) и индуктивное падение напряжения (хК). Измеренные значения напряжения короткого замыкания U1к, мощность потерь короткого замыкания РК и тока I1H, позволяют определить параметры схемы замещения (RК - активное сопротивление, хК - индуктивное сопротивление, zК - полное сопротивление, а также коэффициент мощности при коротком замыкании), точно также, как это делали при обработке экспериментальных данных опыта холостого хода, и при выполнении работы ”Последовательная цепь переменного тока”.
uК - напряжение короткого замыкания, выраженное в процентах от номинального, обычно заносится в паспорт трансформатора.
3. Опыт нагрузки.
Коэффициентом загрузки - называется отношение тока, протекающего в обмотках трансформатора, к номинальному току той же обмотки. Активная мощность Р2 передаваемая в нагрузку равна активной мощности Р1, измеренной экспериментально, за вычетом всех потерь мощности.
Преобразование энергии в трансформаторе сопровождается потерями энергии на перемагничивание сердечника и нагрев обмоток.
Потери в сердечнике для данного трансформатора постоянны, не зависят от нагрузки и определяются в опыте холостого хода, т.е.:
|
(7) |
Потери в медных обмотках пропорциональны квадрату коэффициента загрузки:
|
(8) |
Коэффициент мощности - cos1 определяется соотношением активной мощности Р1 к полной U1I1. Коэффициент полезного действия - отношение активной мощности передаваемой в нагрузку к активной мощности, получаемой трансформатором из сети.
7. Содержание отчета
Наименование и цель работа.
Технические данные оборудования и электроизмерительных приборов.
Схема экспериментальной установки.
Таблицы экспериментальных и расчетных данных.
Расчетные формулы.
Рабочие характеристики трансформатора.
Выводы.
Содержание графической части и выводов
Постройте графики зависимости вторичного напряжения - U2, мощности - Р2, коэффициента мощности cos1 и коэффициента полезного действия - от коэффициента загрузки. Укажите экспериментальные значения коэффициента трансформации, тока холостого хода в процентах, потерь мощности в стальном сердечнике, напряжения короткого замыкания в процентах и потерь мощности в обмотках при номинальной нагрузке.
Сделайте заключение о цели проведения опыта холостого хода.
Сделайте заключение о цели проведения опыта короткого замыкания.
Сделайте вывод о влиянии коэффициента загрузки на величину вторичного напряжения. Рассчитайте по уравнению 6 значение изменения вторичного напряжения в процентах при изменении нагрузки от 0 до номинальной и приведите его значение.
Сделайте вывод о влиянии характера нагрузки на величину вторичного напряжения. (Этот пункт выполняется, если рассчитывались внешние характеристики трансформатора для индуктивной и емкостной нагрузок на ПЭВМ Агат-9).
Сделайте вывод о влиянии коэффициента загрузки на величину КПД трансформатора. Отметьте значение коэффициента загрузки, при котором КПД достигает максимальной величины. Соответствует ли это значение соотношению (8)? Сформулируйте условие, при котором КПД трансформатора достигает максимума.
Сделайте вывод о влиянии характера нагрузки на величину КПД. (Этот пункт выполняется, если рассчитывался КПД трансформатора при индуктивной и емкостной нагрузок на ПЭВМ Агат-9).
Сделайте вывод о влиянии коэффициента загрузки на величины мощности Р2 и коэффициента мощности.
Контрольные вопросы
Какой закон физики положен в основу принципа действия трансформатора?
От каких величин зависят ЭДС первичной и вторичной обмоток трансформатора?
С какой целью проводятся опыты холостого хода и короткого замыкания трансформатора?
Как проводится опыт холостого хода?
Как проводится опыт короткого замыкания?
Что такое коэффициент трансформации?
Как определить коэффициент трансформации экспериментально?
Как определить потери мощности в сердечнике экспериментально?
Как определить потери мощности в обмотках трансформатора при номинальной нагрузке?
При каком условии КПД трансформатора достигает максимального значения?
Техника безопасности при испытании трансформатора
К лабораторному стенду подведено напряжение 220 В - опасное для жизни.
Перед сборкой экспериментальных схем убедитесь, что напряжение на стенде отсутствует (сигнальные лампы не горят, красная кнопка автомата АП утоплена).
Не используйте проводов с поврежденной изоляцией.
Надежно закрепляйте наконечники проводов клеммами, особенно в тех случаях, когда под клеммой находятся несколько наконечников.
КАТЕГОРИЧЕСКИ ЗАПРЕЩАЕТСЯ ВКЛЮЧЕНИЕ СХЕМЫ БЕЗ ПРОВЕРКИ ПРЕПОДАВАТЕЛЕМ ИЛИ ЛАБОРАНТОМ!!!
Все изменения в схеме производятся только при снятии напряжения. Повторное включение схемы производится только после проверки преподавателем или лаборантом.
Во время работы не касайтесь клемм стенда и клемм измерительных приборов.
В случае возникновения аварийных ситуаций (выпадения наконечников проводов из-под клемм, зашкаливания стрелок измерительных приборов, появления дыма или запаха горелой изоляции) немедленно отключите стенд нажатием на красную кнопку автомата АП в правой части стенда.
Лабораторная работа №11 Тема: Определение потерь напряжения в линиях электропередач
Цель работы: определить какие факторы и как они влияют на потери напряжения и мощности. Определить КПД ЛЭП.
1.Пояснение к работе
Краткие теоретические сведения.
О т
генератора до потребителя электроэнергия
передается по проводам, т.е. по линии
электропередачи. Так как ЛЭП характеризуется
определенным сопротивлением, то на нее
тратиться активная мощность на нагрев
проводов. Чем больше сопротивление ЛЭП,
тем больше и потери мощности. На ЛЭП
имеет место и потери напряжения. Чем
больше ток или сопротивление проводов,
тем больше и потери мощности и
напряжения.
Потери электроэнергии
в проводах зависят от силы тока, поэтому
при передаче её на дальние расстояния,
напряжение многократно повышают (во
столько же раз уменьшая силу тока) с
помощью трансформатора, что при передаче
той же мощности позволяет значительно
снизить потери. Однако с ростом напряжения
начинают происходить различные разрядные
явления.В воздушных линиях сверхвысокого
напряжения присутствуют потери активной
мощности на корону (коронный разряд).
Эти потери зависят во многом от погодных
условий (в сухую погоду потери меньше,
а в дождь, изморось или снег эти потери
возрастают) и расщепления провода в
фазах линии.
т
генератора до потребителя электроэнергия
передается по проводам, т.е. по линии
электропередачи. Так как ЛЭП характеризуется
определенным сопротивлением, то на нее
тратиться активная мощность на нагрев
проводов. Чем больше сопротивление ЛЭП,
тем больше и потери мощности. На ЛЭП
имеет место и потери напряжения. Чем
больше ток или сопротивление проводов,
тем больше и потери мощности и
напряжения.
Потери электроэнергии
в проводах зависят от силы тока, поэтому
при передаче её на дальние расстояния,
напряжение многократно повышают (во
столько же раз уменьшая силу тока) с
помощью трансформатора, что при передаче
той же мощности позволяет значительно
снизить потери. Однако с ростом напряжения
начинают происходить различные разрядные
явления.В воздушных линиях сверхвысокого
напряжения присутствуют потери активной
мощности на корону (коронный разряд).
Эти потери зависят во многом от погодных
условий (в сухую погоду потери меньше,
а в дождь, изморось или снег эти потери
возрастают) и расщепления провода в
фазах линии.
Потери на корону для линий различных напряжений имеют свои значения (для линии ВЛ 500 кВ среднегодовые потери на корону составляют около ΔР=9–11 кВт/км).
Так как коронный разряд зависит от напряжённости на поверхности провода, то для уменьшения этой напряжённости в воздушных линиях сверхвысокого напряжения применяют расщепление фаз. То есть вместо одного провода применяют два и более проводов в фазе. Располагаются эти провода на равном расстоянии друг от друга. Получается эквивалентный радиус расщеплённой фазы, этим уменьшается напряжённость на отдельном проводе, что в свою очередь уменьшает потери.
В ГОСТ 13109-97 говорится, что нормальное отклонение напряжения не должно превышать 5, а предельное – 10 процентов.
2.Техническое задание
2.1.Собрать электрическую цепь (рисунок 1).

Рисунок 1 - Схема электрическая принципиальная.
2.2.Снять показания приборов и записать их в таблицу.
2.3.Произвести расчеты.
2.4.Ответить на контрольные вопросы.
2.5. Сделать вывод.
3.Работа в лаборатории.
3.1. Собрать схему (Рисунок 2).
 Рисунок
2 - Схема исследования.
Рисунок
2 - Схема исследования.
3.2. Подать на начало ЛЭП (S=1 мм2, L=1000 м) напряжение 220В и подключить нагрузку Rн = 1 кОм, материал проводов выбрать согласно варианта (таблица 1).
3.3. Замерить напряжение на выходе ЛЭП и ток.
3.4. Записать измеренные величины в таблицу 2.
3.5. Произвести расчеты и сделать вывод.
Табличные значения удельных сопротивлений находятся тут.
Таблица 1 – Варианты
№ варианта |
1 опыт |
2 опыт |
3 опыт |
1 |
Висмут |
Латунь |
Свинец |
2 |
Вольфрам |
Манганин |
Серебро |
3 |
Железо |
Медь |
Цинк |
4 |
Золото |
Молибден |
Алюминий |
5 |
Константан |
Никель |
Висмут |
6 |
Латунь |
Нихром |
Вольфрам |
7 |
Манганин |
Олово |
Железо |
8 |
Медь |
Платина |
Золото |
9 |
Молибден |
Свинец |
Константан |
10 |
Никель |
Серебро |
Латунь |
11 |
Нихром |
Цинк |
Манганин |
12 |
Олово |
Алюминий |
Медь |
13 |
Платина |
Висмут |
Молибден |
14 |
Свинец |
Вольфрам |
Никель |
15 |
Серебро |
Железо |
Нихром |
Таблица 2 - Результаты измерений.
№ опыта |
Измерения |
Расчет |
Материал проводов |
|||||
U1 |
U2 |
I |
∆U′ |
∆P′ |
η |
Rпр |
||
В |
В |
А |
В |
Вт |
% |
Ом |
||
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|

4. Содержание отчета
4.1. Название и цель работы
4.2. Схемы
4.3. Таблицы
4.4. Ответы на контрольные вопросы
4.5. Вывод
5.Контрольные вопросы.
5.1. Какая допускается потеря напряжения по госту в силовой линии и линии освещения?
5.2. Какой металл лучше всего проводит электрический ток?
5.3. От чего зависит потеря напряжения в проводах?
5.4. Почему для нагревательных приборов применяют материалы с большим значением удельного сопротивления?
Лабораторная работа №12 Тема: Исследование и снятие вольт-амперных характеристик полупроводникового диода
Время-2 час
Цель работы – Сформировать знания студентов с основными параметрами и характеристиками полупроводниковых выпрямительных диодов, научить собирать схемы выпрямления.
Общие сведения
Полупроводниковым диодом называют электропреобразовательный полупроводниковый прибор с одним или несколькими p-n-переходами и двумя выводами.
Структура полупроводникового диода с электронно-дырочным переходом и его условное графическое обозначение приведены на рис. 1, а, б.

а б
Рис. 1
Буквами p и n обозначены слои полупроводника с проводимостями соответственно p-типа и n-типа. Обычно концентрации основных носителей заряда (дырок в слое p и электронов в слое n) сильно различаются. Одна из областей p-n-структуры, называемая эмиттером, имеет большую концентрацию основных носителей заряда, чем другая область, называемая базой.
В зависимости от основного назначения и вида используемого явления в p-n-переходе различают шесть основных функциональных типов электропреобразовательных полупроводниковых диодов: выпрямительные, высокочастотные, импульсные, туннельные, стабилитроны, варикапы. Каждый тип диода содержит ряд типономиналов, регламентированных соответствующим ГОСТом.
На рис. 2 представлены структуры планарно-эпитаксиального (а) и сплавного (б) диодов. База и эмиттер образуют омические переходы (контакт) с электродами. К электродам подсоединены металлические выводы, посредством которых диод включается в цепь.

а б
Рис. 2
Основной характеристикой полупроводниковых диодов служит вольт-амперная характеристика. В отличие от характеристики идеального p-n- перехода (пунктирная кривая на рис. 3,а), характеристика реального диода (сплошная кривая на рис. 3,а) в области прямых напряжений U располагается несколько ниже из-за падения части приложенного напряжения на объёмном сопротивлении базы диода r .
Уравнение вольт-амперной характеристики имеет вид:

где
U - напряжение на p-n-переходе; I0
-обратный (или тепловой) ток,
 -
температурный потенциал электрона.
-
температурный потенциал электрона.

а б
Рис. 3
В области обратных напряжений можно пренебречь падением напряжения в объёме полупроводника. При достижении обратным напряжением определённого критического значения ток диода начинает резко возрастать. Это явление называют пробоем диода.
Различают два основных вида пробоя электронно-дырочного перехода:
электрический и тепловой. В обоих случаях резкий рост тока связан с увеличением числа носителей заряда в переходе. Электрический пробой бывает двух видов - лавинный и туннельный.
Полупроводниковые диоды отличаются друг от друга материалом полу-
проводника. Наиболее часто в них используют германий или кремний. Вольт-амперные характеристики кремниевого и германиевого диодов представлены на рис. 3,б. При повышении температуры абсолютная величина изменения обратного тока в кремниевом диоде (рис. 4,а) значительно меньше, чем в германиевом (рис. 4,б).

а б
Рис. 4
Выпрямительные диоды используют для выпрямления переменных токов частотой 50 Гц – 100 кГц. В них используется главное свойство p-n-перехода – односторонняя проводимость. Главная особенность выпрямительных диодов большие площади p-n-перехода, поскольку они рассчитаны на выпрямление больших по величине токов. Основные параметры выпрямительных диодов даются применительно к их работе в однополупериодном выпрямителе с активной нагрузкой (без конденсатора, сглаживающего пульсации).
Среднее прямое напряжение Uпр..ср — среднее за период прямое напряжение на диоде при протекании через него максимально допустимого выпрямленного тока.
Средний обратный ток Iобр. ср — средний за период обратный ток, измеряемый при максимальном обратном напряжении.
Максимально допустимое обратное напряжение Uобр. mах (Uобр. и mах) – наибольшее постоянное (или импульсное) обратное напряжение, при котором диод может длительно и надежно работать.
Максимально допустимый выпрямленный ток Iвп. ср mах — средний за период ток через диод (постоянная составляющая), при котором обеспечивается его надежная длительная работа.
Превышение максимально допустимых величин ведет к резкому сокращению срока службы или пробою диода.
Максимальная частота fтах — наибольшая частота подводимого напряжения, при которой выпрямитель на данном диоде работает достаточно эффективно, а нагрев диода не превышает допустимой величины.
В выпрямительном устройстве энергия переменного тока преобразуется в энергию постоянного тока за счет односторонней проводимости диодов.

Рис.5
На рис. 5 приведена схема однополупериодного выпрямителя. Работа выпрямителя происходит следующим образом. Если генератор вырабатывает синусоидальное напряжение,
e(t) = Еm sin w t,
то в течение положительного (+) полупериода напряжение для диода является прямым, его сопротивление мало, и через резистор проходит ток, который создает на резисторе RН падение напряжения Uвых , повторяющее входное напряжение e(t). В следующий, отрицательный (-) полупериод, напряжение для диода является обратным, сопротивление диода велико, тока практически нет и, следовательно, Uвых = 0. Таким образом, через диод и RН протекает пульсирующий выпрямленный ток. Он создает на резисторе RН пульсирующее выпрямленное напряжение Uвых .
Полезной частью выпрямленного напряжения является его постоянная составляющая или среднее значение U ср (за полупериод):
Ucp = Umax / =0,318 Umax
Таким образом, U ср составляет около 30% от максимального значения.
Выпрямленное напряжение обычно используется в качестве напряжения питания электронных схем.
Высокочастотные (универсальные) и импульсные диоды применяют для выпрямления токов, модуляции и детектирования сигналов с частотами до нескольких сотен мегагерц. Импульсные диоды используют в качестве ключевых элементов в устройствах с микросекундной и наносекундной длительностью импульсов. Их основные параметры:
Максимально допустимые обратные напряжения Uобр. mах (Uобр. и mах) – постоянные (импульсные) обратные напряжения, превышение которых приводит к его немедленному повреждению.
Постоянное прямое напряжение Uпр – падение напряжения на диоде при протекании через него постоянного прямого тока Iпр – заданного ТУ.
Постоянный обратный ток Iобр — ток через диод при постоянном обратном напряжении (Uобр мах). Чем меньше Iобр , тем качественнее диод.
Емкость диода Сд — емкость между выводами при заданном напряжении. При увеличении обратного напряжения (по модулю) емкость Сд уменьшается.
При коротких импульсах необходимо учитывать инерционность процессов включения и выключения диода, что характеризуется следующими параметрами.
1) Время установления прямого напряжения на диоде (tуст ) – время, за которое напряжение на диоде при включении прямого тока достигает своего стационарного значения с заданной точностью (рис. 6,а).
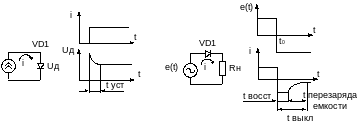
а б
Рис. 6
Это время связанно со скоростью диффузии и состоит в уменьшении сопротивления области базы за счёт накопления в ней неосновных носителей заряда, инжектируемых эмиттером. Первоначально оно высоко, т.к. мала концентрация носителей заряда. После подачи прямого напряжения концентрация неосновных носителей заряда в базе увеличивается, это снижает прямое сопротивление диода.
2) Время восстановления обратного сопротивления диода (tвосст.) определяется как время, в течение которого обратный ток диода после переключения полярности приложенного напряжения с прямого на обратное достигает своего стационарного значения с заданной точностью (рис. 6, б), обычно 10% от максимального обратного тока. Это время связано с рассасыванием в базе неосновных носителей заряда, накопленных при протекании прямого тока. Оно состоит из двух составляющих tвосст.= t1.+ t2., где t1. – время рассасывания, за которое концентрация неосновных носителей заряда на границе р-п-перехода обращается в ноль; t2. – время разряда диффузионной емкости, связанное рассасыванием неосновных зарядов в объеме базы диода. В целом время восстановления это время выключения диода.
Там, где требуется малое время переключения, используют диоды Шотки. Они имеют переход металл — полупроводник, который обладает выпрямительным эффектом. Накопление заряда в переходе этого типа выражено слабо. Поэтому время переключения может быть уменьшено до значения порядка 100 пс. Другой особенностью этих диодов является малое (по сравнению с обычными кремниевыми диодами) прямое напряжение, составляющее около 0,3 В.
Задание
Расчетная часть
Рассчитать вольт-амперную характеристику (ВАХ) выпрямительного диода I=f(U) при температуре окружающей среды +200С и +400С в диапазоне U=0…300мВ (не менее 5 точек).
Ток
диода при прямом напряжении U:
 ,
,
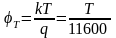 ,
,
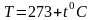 ,
,
 ,
,
где
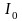 - обратный ток диода,
- обратный ток диода,
- температурный потенциал электрона,
k - постоянная Больцмана,
q - заряд электрона.
Определить дифференциальное сопротивление и сопротивление диода постоянному току в начале линейного участка ВАХ при температуре окружающей среды +200С и +400С соответственно.
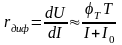 ,
.
,
.
Исходные данные к расчету
Выпрямительный
диод Д223А,
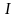 макс=50мA,
=1мкA
(
макс=50мA,
=1мкA
(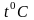 =20
=20 ).
).
Экспериментальная часть
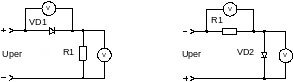
а б
Рис.7
Исследовать полупроводниковые выпрямительные диоды VD1, VD2 рис. 7,а,б:
cнять вольт-амперные характеристики (ВАХ) диодов VD1, VD2 I=f(U),
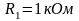 (не менее 10 точек);
(не менее 10 точек);результаты оформить в виде таблиц 1, 2 и графиков.
Таблица 1
-
Прямая
ветвь
UVD1
[B]
UR1
[B]
IVD1
[mA]
Обратная ветвь
UVD1
[B]
UR1
[B]
IVD1
[mA]
Таблица 2
-
Прямая
ветвь
UVD2
[B]
UR1
[B]
IVD2
[mA]
Обратная ветвь
UVD2
[B]
UR1
[B]
IVD2
[mA]
по результатам определить типы используемых выпрямительных диодов (кремниевый или германиевый);
определить значение емкостей диодов Cд1, Сд2 при обратном напряжении Uобр=4В.
Исследовать схему однополупериодного выпрямителя рис. 7,а:
зарисовать осциллограммы напряжений на входе и выходе выпрямителя при подаче на вход синусоидального колебания заданной амплитуды и частоты;
зарисовать осциллограммы напряжений на входе и выходе выпрямителя при подаче на вход колебания типа “меандр” заданной амплитуды и частоты.
Исследовать схему диодного амплитудного ограничителя рис. 7,б:
зарисовать осциллограммы напряжений на входе и выходе амплитудного ограничителя при подаче на вход синусоидального колебания заданной амплитуды и частоты;
зарисовать осциллограммы напряжений на входе и выходе амплитудного ограничителя при подаче на вход колебания типа “меандр” заданной амплитуды и частоты;
по результатам определить порог ограничения для данного амплитудного ограничителя рис. 7,б.
Описание лабораторной установки
Принципиальная схема макета, представленная на рис. 7, позволяет изучить основные свойства кремниевого и германиевого полупроводниковых диодов. Для снятия прямой и обратной ВАХ диодов на схемы подается регулируемое напряжение Uрег соответствующей полярности. Схема на рис.7,а позволяет изучить принцип работы однополупериодного выпрямителя. Схема рис.7,б позволяет исследовать амплитудный диодный ограничитель.
Указания по выполнению работы
Для снятия вольт-амперных характеристик (ВАХ) диодов VD1, VD2 необходимо использовать регулируемый стабилизированный источник питания 0-15В, напряжение с которого подключается к клеммам “Uрег” на лабораторном стенде с соответствующей полярностью. Для снятия прямой ветви ВАХ на анод диода подается положительное напряжение Uрег (прямое включение диода). Для снятия обратной ветви ВАХ на анод подается отрицательное напряжение Uрег (обратное включение диода). Изменяя напряжение Uрег с источника питания от нуля до 15В, вольтметром постоянного тока или универсальным вольтметром фиксируют напряжения на диоде и резисторе R1, данные заносятся в таблицу. Значение тока рассчитывается по закону Ома.
Для определения значений емкостей диодов Cд1, Сд2 на схемы рис. 7,а,б подают синусоидальное колебание амплитудой Uвх=4В частотой f=0,3МГц. Обратное для диода напряжение, в данном случае отрицательная полуволна, используется для определения реактивного сопротивления емкости диода на заданной частоте. Схема замещения цепей рис. 7, а, б на высокой частоте для обратного напряжения представляет собой резистивно-емкостной делитель, что позволяет приближенно оценить значения емкостей диодов Cд1, Сд2:
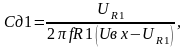
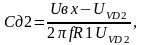
где Uвх – амплитуда входного напряжения,
UR1 – значение обратного напряжения (отрицательной полуволны) на резисторе R1,
UVD2 – значение обратного напряжения на диоде VD2.
Значения Uвх, UR1, UVD2 определяют с помощью осциллографа.
Для исследования схемы однополупериодного выпрямителя на схему рис.7,а последовательно подают синусоидальное колебание и колебание типа “меандр” с генератора низкой частоты. При этом выход генератора подключается к клеммам “Uрег” лабораторного стенда. Значение амплитуд и частот сигналов указывается преподавателем. С помощью осциллографа зарисовать сигналы на входе и выходе однополупериодного выпрямителя.
Для исследования схемы диодного амплитудного ограничителя на схему рис.7,б последовательно подают синусоидальное колебание и колебание типа “меандр” с генератора низкой частоты. При этом выход генератора подключается к клеммам “Uрег” лабораторного стенда. Значение амплитуд и частот сигналов указывается преподавателем. С помощью осциллографа зарисовать сигналы на входе и выходе амплитудного ограничителя. По результатам определить порог ограничения амплитудного ограничителя.
Содержание отчета
Отчет по работе должен содержать:
Цель работы.
Исходные данные для расчета.
Предварительный расчет.
Принципиальную схему лабораторной установки.
Таблицы экспериментальных и расчетных данных.
Графики зависимостей, полученных в результате эксперимента и расчета.
Краткие выводы по результатам расчета и эксперимента.
Контрольные вопросы
Пояснить как образуется p-n-переход.
Свойства p-n-перехода, потенциальный барьер.
Какой из выводов полупроводникового диода называют базой, а какой эмиттером и почему?
Виды полупроводниковых диодов, назначение, область применения, основные параметры и характеристики.
В чем особенность диодов Шотки, их достоинства и область применения.
В чем отличие идеальной ВАХ полупроводникового диода от реальной?
Сравнить ВАХ германиевого и кремниевого полупроводникового диода, сопоставить с полученными экспериментальными данными.
Сравнить по температурным свойствам кремниевый и германиевый полупроводниковые диоды.
Что называют прямым включением диода?
Какой ток протекает через диод при его обратном включении и чем он вызван?
Какое явление называется пробоем диода? Виды пробоя.
Что называют дифференциальным сопротивлением диода?
Пояснить как в лабораторной работе экспериментально снимались ВАХ диодов?
Нарисовать принципиальную схему однополупериодного выпрямителя отрицательного напряжения и осциллограммы сигнала на его входе и выходе.
Нарисовать принципиальную схему амплитудного диодного ограничителя, исследовавшегося в работе, и осциллограммы сигнала на его входе и выходе, пояснить принцип действия.
Чем обусловлен порог ограничения амплитудного диодного ограничителя?
Чем обусловлены инерционные свойства полупроводниковых диодов?
Какие параметры характеризуют инерционность полупроводниковых диодов?
Лабораторная работа №13
Тема: ИССЛЕДОВАНИЕ И СНЯТИЕ ВОЛЬТ-АМПЕРНЫХ ХАРАКТЕРИСТИК ФОТОРЕЗИСТОРА.
Время-2 час
Цель работы
Сформировать знания студентов с принципом и работой фоторезистора, исследовать его основные характеристики, оценить ширину запрещенной зоны полупроводника, из которого сделан фоторезистор.
Содержание
Фоторезистором называется полупроводниковый прибор, действие которого основано на фотопроводимости – изменении проводимости полупроводника при освещении (внутренний фотоэффект). В полупроводнике под действием света генерируются свободные носители заряда ( в отличие от внешнего фотоэффекта, когда электроны под действием света выходят из вещества).
Рассмотрим это явление. В химически чистом (собственном) полупроводнике при абсолютном нуле валентная зона заполнена электронами, а зона проводимости свободна. Неосвещенный полупроводник при абсолютном нуле является изолятором. Если полупроводник нагреть, то вследствие теплового возбуждения появятся электроны в зоне проводимости и дырки в валентной зоне. Электропроводность полупроводника, обусловленная тепловым возбуждением, называется темновой проводимостью:
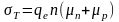 , (1)
, (1)
где
n - концентрация
электронов в зоне проводимости и дырок
в валентной зоне;
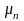 и
и
 - подвижность электронов и дырок
соответственно;
- подвижность электронов и дырок
соответственно;
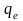 - заряд носителя тока.
- заряд носителя тока.
При
освещении полупроводника возникают
дополнительные носители заряда,
обусловленные внутренним фотоэффектом.
При поглощении кванта света один из
валентных электронов переходит в зону
проводимости, а в валентной зоне
образуется дырка. Очевидно, такой переход
возможен, если энергия фотона
 равна или несколько больше ширины
запрещенной зоны
равна или несколько больше ширины
запрещенной зоны
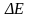 (рис.1а):
(рис.1а):
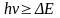 . (2)
. (2)
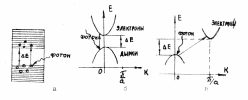
Рис.1.
Аналогично протекает процесс фотоионизации и в примесном полупроводнике. В донорном полупроводнике под действием квантов света электроны переходят с донорных уровней в зону проводимости (рис.2а) , в акцепторных – из валентной зоны на акцепторные уровни (рис.2б).
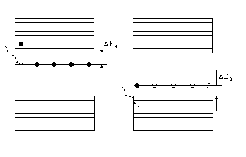
Рис.2.
Очевидно, примесная фотопроводимость возникает при условии
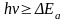 , (3)
, (3)
где
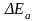 - энергия активации примесных атомов.
Частоту, соответствующую знаку равенства
в выражении (2) называют краем собственного
поглощения, а в выражении (3) – краем
примесного поглощения. Край поглощения
называют также красной границей
внутреннего фотоэффекта.
- энергия активации примесных атомов.
Частоту, соответствующую знаку равенства
в выражении (2) называют краем собственного
поглощения, а в выражении (3) – краем
примесного поглощения. Край поглощения
называют также красной границей
внутреннего фотоэффекта.
Избыточные электроны и дырки, генерируемые при освещении, являются неравновесными носителями заряда в отличие от равновесных носителей, которые имеются в полупроводнике при данной температуре и находятся в термодинамическом равновесии с решеткой кристалла. Дополнительная проводимость, обусловленная появлением неравновесных носителей заряда, и есть фотопроводимость. В случае собственного поглощения фотопроводимость равна
 , (4)
, (4)
где
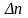 - число пар электрон-дырка, возникающих
при поглощении квантов света.
- число пар электрон-дырка, возникающих
при поглощении квантов света.
При
примесном поглощении появляются
неравновесные носители заряда
преимущественно одного типа. В общем
случае
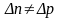 фотопроводимость определяется выражением
фотопроводимость определяется выражением
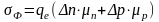 . (5)
. (5)
На величину фотопроводимости влияет также время жизни носителей заряда (промежуток времени от момента генерации носителя заряда до его рекомбинации – соединения электрона и дырки), коэффициент оптического поглощения, квантовый выход внутреннего фотоэффекта (отношение числа генерируемых носителей заряда к числу поглощенных фотонов).
Из сказанного ясно, что полная электропроводность складывается из темновой и фотопроводимости:
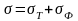 . (6)
. (6)
Методика эксперимента с хематическое устройство фоторезистора дано на рис.3.
Рис.3.
На изолирующую подложку 1 помещается тонкий слой полупроводника 2 (фоточувствительный слой). По краям этого слоя нанесены металлические электроды (контакты) 3. Для предохранения фоточувствительного слоя его покрывают тонкой пленкой лака, прозрачной в области спектральной чувствительности материала. Прибор заключен в закрытый корпус с окном для света. Электроды 3 соединены с клеммами, через которые прибор включается в электрическую цепь последовательно с источником питания.
Основными характеристиками фоторезистора являются вольт-амперная, световая и спектральная.
Вольт-амперной
характеристикой называется зависимость
тока, протекающего через фоторезистор,
от величины приложенного напряжения
при постоянном световом потоке
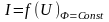 :
:
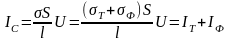 , (7)
, (7)
где
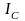 называется световым током;
называется световым током;
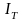 - темновой ток;
- темновой ток;
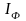 - фототок.
- фототок.
В
частности, если световой поток равен
нулю, то характеристика называется
темновой. Из уравнения (7) видно, что
вольт-амперная характеристика как
темновая, так и при освещении является
линейной, поскольку при постоянной
температуре и постоянном световом
потоке электропроводность не зависит
от напряжения. Следует отметить, что в
области обычно реализуемых освещенностей
световой ток намного больше темнового,
т. е.
 .
.
Световой
характеристикой фоторезистора
называется зависимость фототока от
величины падающего светового потока
при постоянном значении приложенного
напряжения
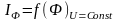 .
Эту зависимость можно заменить
зависимостью
от освещенности Е:
.
Эту зависимость можно заменить
зависимостью
от освещенности Е:
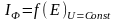 ,
называемой часто люкс-амперной
характеристикой.
,
называемой часто люкс-амперной
характеристикой.
Световая характеристика обычно нелинейная (рис.4). При больших освещенностях увеличение фототока отстает от роста светового потока, намечается тенденция к насыщению. Это объясняется тем, что при увеличении светового потока наряду с ростом концентрации генерируемых носителей заряда растет вероятность их рекомбинации.

Рис.4
Спектральной
характеристикой называется зависимость
фототока от длины волны при постоянной
энергии падающего излучения
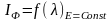 .
Фототок в собственном полупроводнике
появляется, начиная с длины волны
.
Фототок в собственном полупроводнике
появляется, начиная с длины волны
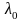 (рис.5), соответствующей равенству
(рис.5), соответствующей равенству
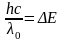 , (8)
, (8)
где - ширина запрещенной зоны полупроводника; - край собственного поглощения. Казалось бы, что спектральная характеристика должна иметь вид ступени (рис.5, кривая «а»), но такой вид она могла бы иметь лишь при абсолютном нуле. При повышении температуры тепловое движение "«размывает» край собственного поглощения (рис.5, кривая «б»).
Р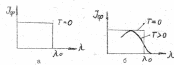 ис.5
ис.5
Вблизи края собственного поглощения у некоторых полупроводников возникает так называемое экситонное поглощение, несколько снижающее величину фототока. (Электрон, возбужденный фотоном, покидает валентную зону, но зоны проводимости не достигает; эта система электрон-дырка, связанная кулоновским взаимодействием, и называется экситоном. Экситоны, будучи нейтральными образованиями, вклада в электропроводность не дают.)
С
увеличением энергии фотона в реальной
спектральной характеристике фототок
быстро достигает максимума, а затем
начинает уменьшаться (рис.5, кривая «б»),
хотя энергии фотона более чем достаточно
для возникновения фотопроводимости.
Это объясняется тем, что с уменьшением
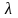 растет коэффициент оптического
поглощения, а это приводит к поглощению
света в тонком приповерхностном слое
вещества, к повышению концентрации
неравновесных носителей и соответственно
повышенной скорости рекомбинации в
этом слое. Другими словами, носители
заряда активно рекомбинируют на
поверхности, не успевая диффундировать
в объеме полупроводника, что приводит
к уменьшению фотопроводимости.
растет коэффициент оптического
поглощения, а это приводит к поглощению
света в тонком приповерхностном слое
вещества, к повышению концентрации
неравновесных носителей и соответственно
повышенной скорости рекомбинации в
этом слое. Другими словами, носители
заряда активно рекомбинируют на
поверхности, не успевая диффундировать
в объеме полупроводника, что приводит
к уменьшению фотопроводимости.
Край
примесного поглощения
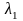 ,
соответствующий равенству
,
соответствующий равенству
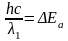 , (9)
, (9)
смещается в сторону больших длин волн относительно собственной фотопроводимости (рис.6). Очевидно, что по спектральной характеристике, определив , можно оценить ширину запрещенной зоны полупроводника, из которого сделан фоторезистор, а определив , - энергию активации примеси.
Р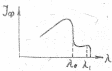 ис.6
ис.6
Фоторезистор характеризуется также такими параметрами как интегральная и спектральная чувствительности. Интегральной удельной чувствительностью называется величина фототока, приходящаяся на единицу потока белого света и на единицу напряжения, приложенного к фоторезистору:
 . (10)
. (10)
Если фоторезистор облучается
монохроматическим светом, то
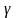 будет спектральной чувствительностью.
будет спектральной чувствительностью.
Фоторезисторы находят широкое применение в различных устройствах автоматизации и контроля.
Введение к выполнению работы
В работе используется фоторезистор СФ2-1, изготовленный из сернистого кадмия. Освещенный фоторезистор представляет собой обычный резистор, сопротивление которого определяется интенсивностью излучения, поэтому его вольтамперная характеристика линейна.
Интенсивность, падающего на фоторезистор излучения, равна:
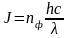 ,
,
где nф – число фотонов падающих на единицу поверхности фоторезистора в единицу времени.
Поскольку фототок пропорционален nф, то он пропорционален и интенсивности.
По спектральной характеристике можно определить ширину запрещенной зоны
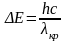 .
.
Задание к работе.
Собрать схему рис.7.
Измерить вольтамперные характеристики фоторезистора при различных значениях интенсивности для двух длин волн. Убедитесь, что зависимости близки к линейной.
Измерьте спектральную характеристику I() при фиксированном значении U.
По спектральной характеристике определите ширину запрещенной зоны.
Измерьте зависимость фототока от интенсивности для двух длин волн.


Рис. 7
Отчет Контрольные вопросы
Что такое внутренний фотоэффект? Сравните с внешним фотоэффектом.
Объясните механизм возникновения фотопроводимости в собственном и примесном полупроводнике.
Что такое край собственного и примесного поглощения? Каким равенствам он удовлетворяет?
Что представляет собой фоторезистор?
Чем объясняется наличие темнового тока фоторезистора?
Объясните ход вольт-амперной и световой характеристик фоторезистора.
Объясните спектральную зависимость фототока в собственной и примесной области поглощения.
Как с помощью спектральной характеристики можно оценить ширину запрещенной зоны полупроводника? Энергию активации примеси?
Что такое интегральная и спектральная чувствительность фоторезистора?
Лабораторная работа № 14
Тема: Исследование и снятие вольт-амперных
Характеристик полупроводникового транзистора
Время -2 час
Цель работы: Сформировать знания студентов с устройством и принципом действия полупроводникового транзистора и получить практические навыки по исследованию входных и выходных характеристик транзистора.
Пояснение к работе
Биполярный транзистор представляет собой трехэлектродный полупроводниковый прибор с двумя электронно-дырочными переходами, имеет три вывода и предназначен для усиления и генерирования электрических сигналов. Электронно-дырочные переходы в транзисторе образуются тремя областями различной электропроводности. В зависимости от порядка чередования областей транзисторы могут быть типов р-п-р и п-р-п. В обоих случаях транзистор содержит два р-п (или п-р)-перехода. На рис. 2.1, а, б показано условное обозначение транзисторов типов р-п-р и п-р-п.
|
|
а) |
б) |
Рис. 2.1. Условные изображения транзисторов разных типов: a) – транзистор типа р-п-р; б) – транзистор типа п-р-п |
|
Крайний, сильно легированный слой с меньшей площадью называется эмиттером, а слой с большей площадью – коллектором. Средний слой транзистора называют базой. Биполярный транзистор можно представить в виде эквивалентной схемы (рис. 2.2.)

Рис. 2.2. Эквивалентная схема биполярного транзистора
Существуют три способа включения транзистора: схема с общей базой (ОБ), общим эмиттером (ОЭ) и общим коллектором (ОК).
Схема ОБ (рис. 2.3) позволяет раскрыть физику транзистора.
|
Рис. 2.3. Включение n-p-n транзистора с общей базой и с общим эмиттером |
Эта схема обладает малым входным сопротивлением и не обеспечивает усиления тока.
Главную роль в транзисторной технике играет включение с общим эмиттером (рис. 2.4)
|
Рис. 2.4. Включение p-n-p транзистора с общей базой и с общим эмиттером |
В схеме с общим эмиттером ток базы управляет током коллектора, в схеме с общим коллектором ток базы управляет током эмиттера. Наиболее часто используют транзисторы при их включении по схеме с общим эмиттером. Входным напряжением в схеме с общим эмиттером является Uбэ. На базе должно быть отрицательное напряжение (в случае транзистора тина р-n-р, чтобы первый переход оказался открытым). Выходным напряжением здесь является Uкэ. Напряжение на коллекторе также должно быть отрицательным относительно эмиттера, а чтобы второй переход был закрытым, напряжение на коллекторе по модулю должно превышать напряжение на базе.
Принцип действия транзистора, включенного по схеме с общим эмиттером, показан на рис. 2.5.
Представим себе структуру транзистора типа n-р-n, включенного по схеме ОЭ (рис.2.5, а). Условное обозначение такого транзистора приведено на рис. 2.5, б. Для удобства отсчета потенциалов эмиттер транзистора заземлим. Входным электродом транзистора является база р-типа, выходным – коллектор n-типа. В соответствии с изложенным ранее между базой и эмиттером подается небольшое положительное напряжение Uбэ, а между коллектором и эмиттером напряжение Uкэ также положительное и большее, чем Uбэ (несколько вольт). Тогда на переходах транзистора получаются напряжения, соответствующие его работе в усилительном режиме.

a) |
б) |
Рис.2.5. Транзистор типа n-р-n:
а) – структура; б) – условное обозначение
При подаче указанных напряжений в структуре транзистора происходят следующие явления. Поскольку на эмиттерный p-n-переход подано прямое напряжение, возникает инжекция, т. е. введение электронов из эмиттера в базу. Одновременно инжектируют и дырки из базы в эмиттер, но этим явлением можно пренебречь, т. к. база имеет меньшую концентрацию примесей по сравнению с эмиттером, а, следовательно, и меньшую концентрацию носителей заряда. Небольшая часть инжектированных электронов (1–3 %) рекомбинирует с дырками базы. За счет этого по проводу, соединенному с базой, будет протекать небольшой ток базы Iб. Остальная часть электронов (α = 0,97÷0,99) проникает далее в коллектор. Этому способствует положительный заряд коллектора, а также то, что базу намеренно выполняют очень тонкой (порядка 1 мкм).
Из такого рассмотрения легко понять механизм усиления схемы ОЭ по току и напряжению. Действительно, пусть за счет входного переменного сигнала напряжение Uбэ изменяется. Это приведет к значительным колебаниям инжектированного эмиттером тока. Наиболее значительная часть этого тока будет протекать в коллектор, а на долю базы опять будет приходиться только небольшая часть тока. Это означает, что хотя входной ток базы небольшой, однако он вызывает значительные колебания тока на выходе. Если же в коллекторную цепь включить резистор с достаточно большим сопротивлением, то в соответствии с законом Ома колебания тока вызовут увеличение амплитуды колебания напряжения, т. е. произойдет усиление сигнала и по току, и по напряжению. Поскольку полярность напряжений, подаваемых на базу и коллектор, положительная, обе цепи можно питать от одного источника, на базу напряжение подают с помощью делителя, т. к. оно должно быть небольшим.
Параметры транзистора можно определить по его входным и выходным характеристикам. Входные характеристики транзистора, включенного по схеме с общим эмиттером, представляют собой зависимости тока базы от напряжения на базе:
Iб = f(Uбэ) при Uкэ = const.
На рис. 2.6 приведены входные характеристики транзистора при его включении с общим эмиттером.

Рис. 2.6. Входная характеристика транзистора
При открытом первом переходе ток базы Iб (т. е. входной ток) сильно зависит от прямого напряжения на базе Uбэ и мало зависит от обратного напряжения Uкэ (при его большом значении).
При увеличении обратного напряжения Uкэ входная характеристика немного смещается вниз, что объясняется уменьшением тока базы из-за увеличения тока коллектора.
Используя входную характеристику транзистора, можно определить его входное сопротивление Rвх для определенного положения рабочей точки А (см. рис. 2.6). Для этого при постоянном напряжении на коллекторе Uкэ задают приращение тока базы ∆Iб и определяют получающееся при этом изменение напряжения на базе ∆Uбэ. Входное сопротивление транзистора определяют как отношение
Rвх = ∆Uбэ / ∆Iб.
Выходные характеристики транзистора, включенного по схеме с общим эмиттером, представляют собой зависимости коллекторного тока от напряжения на коллекторе:
Iк = f(Uкэ) при Iб = const.
На рис. 2.7 приведены выходные характеристики транзистора включенного по схеме с общим эмиттером.
С увеличением тока базы Iб характеристики смещаются вверх. Связь между током коллектора Iк и током базы Iб определяется коэффициентом передачи тока базы β = ∆Iк /∆Iб, который легко можно выразить через известный коэффициент передачи тока эмиттера а:
β = ∆Iк /∆Iб = ∆Iк /(∆Iэ-∆Iк) = а /(I - а).
Коэффициент передачи тока базы β зависит от напряжения на коллекторе Uкэ и от тока эмиттера Iэ.


Рис. 2.7. Выходные характеристики транзистора
При малых напряжениях на коллекторе ׀Uкэ׀ < ׀Uбэ׀ транзистор переходит в режим насыщения, при котором неосновные заряды инжектируются в базу не только эмиттером, но и коллекторным переходами. Для сохранения тока базы неизменным (т. к. характеристики снимают при Iб = const) нужно уменьшить напряжение на базе, что приводит к резкому уменьшению токов эмиттера и коллектора. В этом месте выходные характеристики имеют резкий спад, коэффициент передачи тока базы β резко уменьшается, эффективность управления коллекторным током снижается.
По выходным характеристикам можно определить также выходное сопротивление транзистора Rвыx. Для этого в рабочей точке А при Iб = const задают приращение коллекторного напряжения ∆Uкэ и определяют получающееся при этом приращение тока коллектора ∆Iк. Выходное сопротивление транзистора находят как отношение:
Rвых=∆Uкэ/∆Iк.
Задание
Собрать схему лабораторной установки.
Снять семейство статических характеристик транзистора.
Предварительная подготовка
Изучить устройство и принцип действия биполярного транзистора.
Начертить схему установки и таблицу для снятия характеристик.
Работа в лаборатории
1. Собрать схему лабораторной установки для снятия статических характеристик транзистора (рис. 2.8).
2. Установите на блоке питания переключатель «0–30 V», «0–6,3 V» в положение «–».
3. Подключите схему к клеммам питания « - 0–30 V» и «- 0–6,3 V» штатива приборного.
|
Рис. 2.8. Схема лабораторной установки: ИП1 – вольтметр постоянного тока 3 V; ИП2 – миллиамперметр постоянного тока 10 mА; ИПЗ – миллиамперметр постоянного тока 300 mА; ИП4 – вольтметр постоянного тока 15 V; VТ – транзистор КТ801В. |
4. Изменяя напряжение базы Uб от 0 до 1V, измерьте по прибору ИП2 ток базы Iб для двух фиксированных значений коллекторного напряжения: Uк = 0; Uк = 6V.
5. Изменяя коллекторное напряжение Uк от 0 до 10 V, измерьте по прибору ИПЗ коллекторный ток Iк для двух фиксированных значений тока базы:
Iб = 2 мА; Iб = 4мА.
Показания приборов свести в таблицы 2.2, 2.3.
Таблица 2.1
Uкэ = 0В |
|||||||
Uбэ, Вт |
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1 |
Iб, мкА |
|
|
|
|
|
|
|
Uкэ = 6В |
|||||||
Uбэ, mВ |
|
|
|
|
|
|
|
Iб, mкА |
|
|
|
|
|
|
|
Таблица 2.2
Uкэ, В |
Iб, мА |
|
2 |
4 |
|
Iк, мА |
||
|
|
|
7. По данным измерений постройте графики зависимости:
Iб = f(Uб) при UK = const,
Iк = f (Uк) при Iб = const.
8. Для заданной преподавателем рабочей точки определить выходное сопротивление транзистора.
Содержание отчета
1. Перечень и номинальные данные используемой аппаратуры.
2. Схема лабораторной установки.
3. Входные и выходные характеристики исследованного транзистора.
4. Экспериментальное определение характеристики исследованного транзистора.
5. Экспериментальное определение параметров транзистора в рабочей точке.
6. Выводы.
Контрольные вопросы
Объяснить принцип действия транзистора.
Привести возможные схемы включения транзистора.
Как определить параметры транзистора с помощью входных и выходных характеристик?

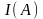
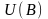
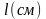
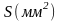
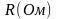
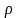
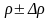
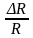
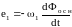 ;
;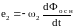 .
.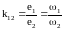 .
.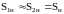 .
.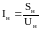
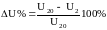 .
.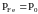 .
.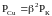 .
.