12. Многочлены над числовыми полями. Основная теорема алгебры.

Определение 16. Множество М называется числовым, если М ℂ.

Поле F называется числовым, если оно является числовым множеством, F ℂ.

Основными числовыми полями являются ℚ, ℝ, ℂ.

Определение 17. Поле F называется алгебраически замкнутым, если любой многочлен положительной степени над полем F имеет хотя бы один корень, принадлежащий полю F.

Теорема 13. Поле F является алгебраически замкнутым любой многочлен положительной степени над полем F разлагается на линейные множители над полем F.

Теорема 14 (Основная теорема алгебры). Всякий многочлен положительной степени над полем ℂ имеет хотя бы один комплексный корень.

Следствие 14.1. Поле ℂ является алгебраически замкнутым.

Следствие 14.2. Любой многочлен положительной степени над полем ℂ разлагается на линейные множители над полем ℂ.

13. Корни многочленов над числовыми полями.

Теорема 15. (необходимый признак рационального корня многочлена с целыми коэффициентами) Пусть ∈ ℤ[x], , - несократимая рациональная дробь. Если - корень f(x), то q, p.

Доказательство. Так как - корень f(x), то f( )=0, то есть:

(1).

Так как 0 , то q . Так как 0 , то p . Теорема доказана.

Следствие 15.1. Рациональные корни нормированного многочлена с целыми коэффициентами являются его целыми корнями.

Следствие 15.2. Целые корни многочлена с целыми коэффициентами являются делителями свободного члена.

Теорема 16. (общий необходимый признак рационального корня многочлена с целыми коэффициентами) Пусть ∈ ℤ[x], , - несократимая рациональная дробь. Если - корень f(x), то , .

Доказательство. Пусть - корень f(x) Пусть . По теореме Безу f(x)=(x-c)q(x)+f(c) (1). Пусть q(x)=

.

Покажем, что . Допустим, что (q, p-cq)=d > 1 - противоречие . Теорема доказана.

Следствие 16.1. Пусть f(x) ℤ[x] , - несократимая рациональная дробь. Если - корень f(x), то .

Приближенные вычисления действительных корней многочлена над ℝ

В 1799 году итальянский математик Руффини доказал (с “пробелом”, не полностью), что всякое алгебраическое уравнение выше 4-ой степени неразрешимо, то есть нельзя найти в общем виде корни уравнения над ℂ выше 4-ой степени. В 1824 году норвежский математик Абель дал полное доказательство неразрешимости алгебраических уравнений выше 4-ой степени. (В алгебре это утверждение известно как теорема Руффини-Абеля). В связи с теоремой Руффини-Абеля на практике возникла потребность отыскания приближенных корней уравнения выше 4-ой степени с действительными коэффициентами.

На первом этапе важно оценить, в какой интервал попадут действительные корни уравнения.

Теорема 17. (Границы корней)

Пусть f(x)= ℝ[x], a₀≠0. Если yℝ – корень многочлена f(x), тогда

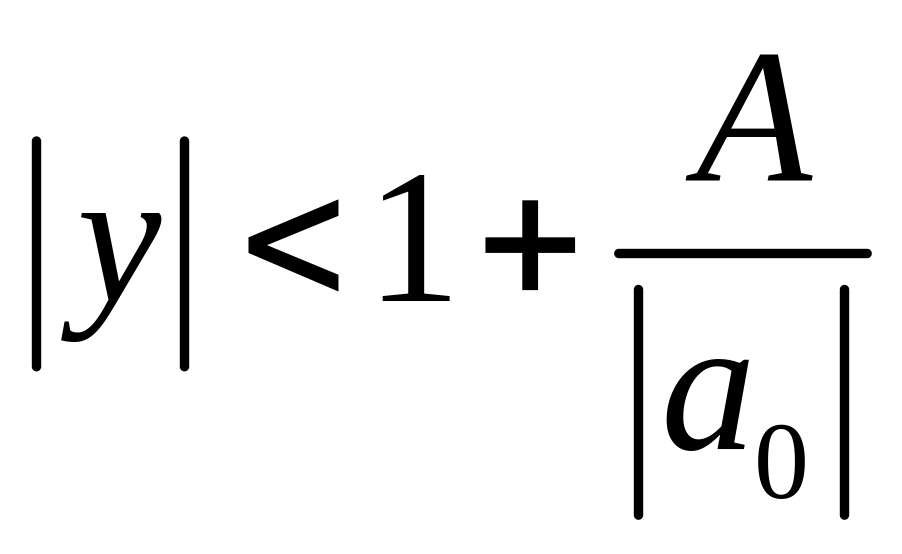1. , где .

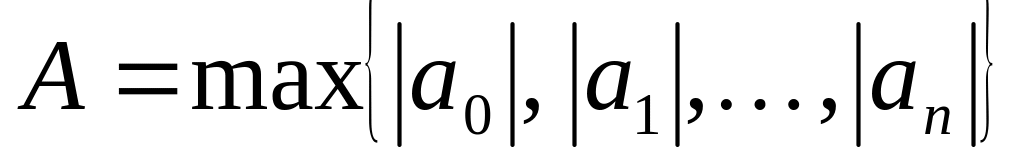Эта граница выполнима и для комплексных корней.

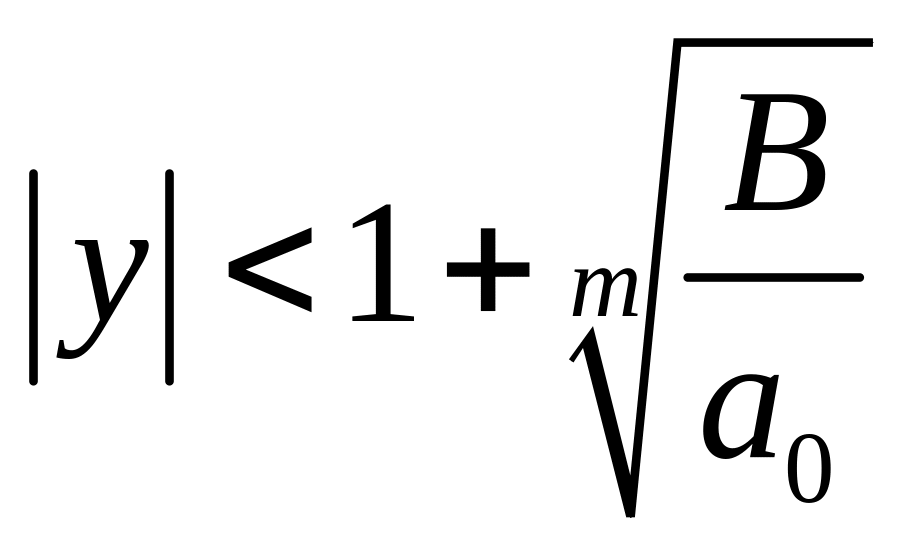2. , где 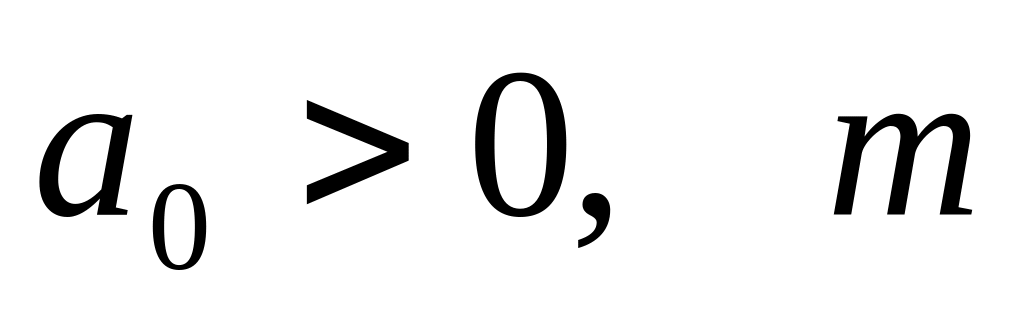– индекс первого отрицательного коэффициента многочлена f(x) , то есть 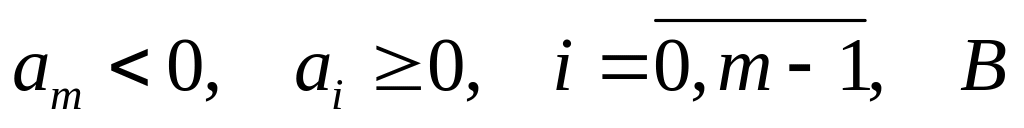- наибольшая из абсолютных величин всех отрицательных коэффициентов f(x).

13