5. Теорема о наибольшем возможном числе корней многочлена над областью целостности

Теорема 5. Пусть K – область целостности, f(x)=а₀+а₁х+а₂х²+…+а_nxⁿ K[x], а_n 0. Тогда многочлен f(x) имеет не более n попарно различных корней. Другими словами, любой ненулевой многочлен n-й степени над областью целостности имеет не более n попарно различных корней.

Доказательство. Доказательство проведём методом математической индукции по параметру n.

1) Пусть n=0 f(x)=a₀ f не имеет корней, т.е. f имеет нуль корней и значит 0 0=n - верно.

2) Пусть n >0. Предположим, что утверждение верно при n=l.

3) Докажем, что утверждение верно при n=l+1: deg f =l+1. Если f не имеет корней, то число корней равно 0 и 0 l+1 - верно. Пусть f имеет хотя бы один корень и с₁ – корень f(x) такой, что с₁ K. Тогда по теореме Безу f(x)=(x-c₁)q(x), где q(x) K[x], причём degq(x)=n-1=l по пункту 2) q(x) имеет не более l попарно различных корней.

Покажем, что все корни многочлена f(x), отличные от с₁, являются также корнями многочлена q(x). Пусть с₂ – корень f(x), с₂ с_{1 =}(c₂-c₁)q(c₂), т.е. (с₂-с₁)q(c₂)=0 (так как K - область целостности) q(c₂)=0 c₂ - корень q(x). Таким образом, многочлен f(x) имеет корень с₁, а все остальные корни многочлена f являются также корнями многочлена q. Так как q(x) имеет не более l попарно различных корней, то многочлен f имеет не более, чем (l+1) попарно различных корней.

Из 1)-3) по методу математической индукции следует, что утверждение верно для любого n N . Теорема доказана.

Следствие 5.1. Пусть K – область целостности, f(x)=а₀+а₁х+а₂х²+…+а_nxⁿ K[x]. Если многочлен f(x) имеет более n попарно различных корней, то f(x) является нулевым многочленом.

7. Теорема о делении с остатком для многочленов

Теорема 6 (о делении с остатком для многочленов) Пусть F – поле, f(x), g(x) F[x], g(x) 0. Тогда существуют единственные многочлены q(x), r(x) F[x] такие, что f(x)=g(x)·q(x)+r(x), причем deg r(x)<deg g(x) (1).

При этом q(x)·называется неполным частным, а r(x) – остатком при делении f(x) на g(x).

Доказательство. 1. Существование.

Если f(x)=0, (1) примет вид 0(x)=g(x)·0(x)+0(x) q(x)=0, r(x)=0, причем deg r(x)= − < deg g(x) 0.

Если deg f(x)<deg g(x) справедливо f(x)=g(x)·0(x)+f(x) в (1) достаточно взять q(x)=0, r(x)=f(x), причем deg r(x)=deg f(x)<deg g(x).

Пусть f(x) 0 и deg f(x) deg g(x). Тогда f(x)=a_o+a₁x+…+a_nxⁿ, g(x)=b_o+b₁x+…+b_mx^m и n m. Доказательство проведем методом математической индукции по параметру n.

1) Пусть n= deg f(x)=0 f(x)=a₀. Так как m≤n=0 и m=deg g(x)-, то m=0 g(x)=b₀ Так как F – поле и b₀0, то существует b₀^-1F. Тогда , причем deg r(x)= − <0=deg g(x).

2) Предположим, что утверждение верно для любого многочлена степени, меньшей n, то есть любой многочлен степени, меньшей n, имеет представление вида (1) , то есть делится на g(x) c остатком.

3) Докажем утверждение для многочлена степени n. Рассмотрим многочлен h(x)=f(x) - b_m^-1∙a_nx^n-m⋅g(x)= (a_o+…+a_nxⁿ ) - b_m^-1∙a_nx^n-m⋅(b_o+…+b_mx^m) = a_o+…+a_nxⁿ- b₀b_m^-1a_nx^n-m -…-b_mb_m^-1a_nx^mx^n-m= a_o+…+a_nxⁿ- b₀b_m^-1a_nx^n-m -…- a_nxⁿ.

Таким образом, старший член степени n многочлена h(x) уничтожается, и h(x) - многочлен степени, меньшей n. По предположению индукции, h(x) делится на g(x) с остатком, то есть q₁(x), r₁(x) F[x]: h(x)=g(x)∙q₁(x)+r₁(x), где deg r₁(x)<deg g(x)

f(x)-b_m^-1∙a_nx^n-m⋅g(x)=g(x)∙q₁(x)+r₁(x) 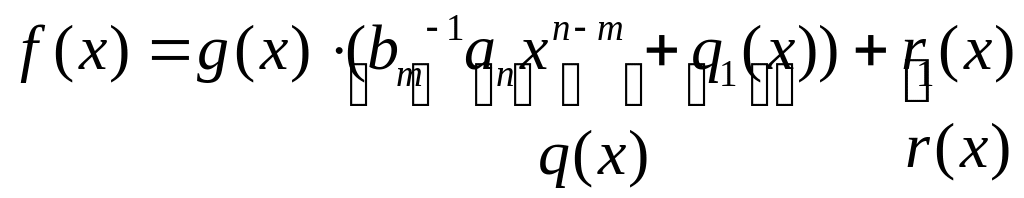, причем deg r(x)<deg g(x). Значит, для f(x) существует деление на g(x) с остатком вида (1).

Из 1)-3) по методу математической индукции следует, что утверждение верно .

2. Единственность. Пусть

f(x)=g(x)∙q₁(x)+r₁(x) (1) и

f(x)=g(x)∙q₂(x)+r₂(x) (2).

Покажем, что q₁=q₂, r₁=r₂. Вычтем из равенства (1) равенство (2): 0=g(x)(q₁-q₂)+(r₁-r₂) r₂-r₁=g(x)(q₁-q₂) (3).

Допустим, что q₁-q₂ 0. Согласно теореме 3, F[x] - область целостности. Поэтому в F[x] нет делителей нуля и из (3) следует, что . Тогда, с одной стороны,

deg(r₂-r₁) 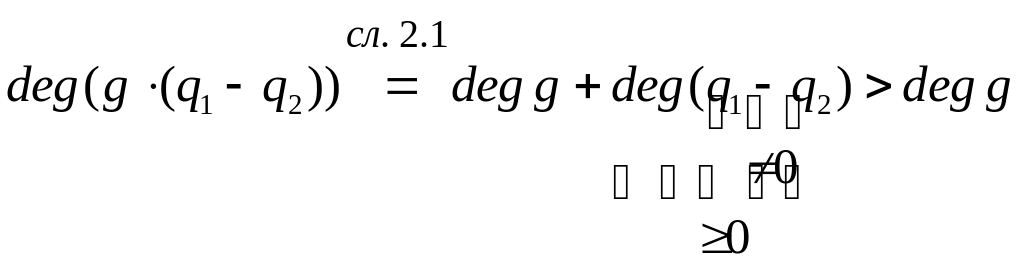, т.е. .

С другой стороны, , т.е. deg(r₂-r₁)<deg g.

Противоречие. Следовательно, . Значит, .

Теорема доказана.