
Лабораторная работа № 5 обработка одномерных и двумерных массивов
Цель работы: разработка, отладка и тестирование программ, осуществляющих ввод, вывод и обработку массивов.
Теория. Массив — структура данных для представления упорядоченного множества элементов одного типа. Для работы с массивом его необходимо описать в блоке VAR следующим образом:
<имя> : ARRAY [1.. <размерность>] OF <тип>,
где <имя> — имя описываемого массива, <размерность> — количество элементов в массиве, <тип> — любой из типов данных, к которому будут принадлежать все элементы массива.
П р и м е р
A : ARRAY [1..100] OF REAL;
B : ARRAY [1..10,7..20] OF INTEGER;
Обращение к элементу массива происходит через указание имени массива и записи в квадратных скобках через запятую конкретных индексов. Обращение к элементу A32 записывается так: A[3,2].
Задания
Задание 1 Cоставить программу формирования массива исходных данных и выполнения задания в соответствии с вариантом табл. 5.1.
Т а б л и ц а 5.1.
№ п/п |
Задание
|
Контрольный результат |
||||||||||||||||
1 |
2 |
3 |
||||||||||||||||
Вариант 1 |
||||||||||||||||||
1 |
В
массиве
|
|
||||||||||||||||
2 |
Сформировать
матрицы
А,
В,
С:
и
выполнить
|
|
||||||||||||||||
Продолжение табл. 5.1
1 |
2 |
3 |
||||||||||||||||
3 |
Дан вектор А(10) = {1, –107, –23, 5, –120, –15, 17, 160, 66, 41}. Поменять местами последний и минимальный элементы данного вектора |
(1, –107, –23, 5, 41, –15, 17, 160, 66, –120) |
||||||||||||||||
4 |
В массиве заменить наибольший элемент удвоенным наименьшим |
|
||||||||||||||||
5 |
Дана матрица A(4, 4) = ((54, 81, 19, 43), (3, –44, 42, 51), (76, 5, 29,–24), (94, –92, –69, 28)). Найти максимальный элемент в каждой из ее строк |
81, 51, 76, 94 |
||||||||||||||||
Вариант 2 |
||||||||||||||||||
1 |
Дана матрица A(4, 4) = ((1, 8, 9, 3), (3, -4, 2, 1), (6, 5, 9, –4), (9, –9, –9, 2)). Найти сумму элементов, стоящих в первом столбце в данной матрице |
82 |
||||||||||||||||
2 |
Сформировать
матрицы А,
В:
|
|
||||||||||||||||
3 |
Дан вектор А(10) = {10,–17, –3,5, –10, –5, 7, 10, 6, 1}. Поменять в этом векторе максимальный и минимальный элементы местами |
(–17, 10, –3, 5 , –10, –5, 7, 10, 6, 1) |
||||||||||||||||
4 |
Дан вектор А(10) = {12, –1, –2, 35, –13, –55,7, –10, 5, 12}. Найти среднее геометрическое между максимальным и минимальным элементами данного вектора |
–962,5 |
||||||||||||||||
5 |
Дана матрица A(4, 4 ) = ((54, 81, –19, 43), (3, –44, 42, 51), (76, 5, 29, –24), (94, –92, –69, 28). Найти минимальный элемент в данной матрице |
–92 |
||||||||||||||||
Вариант 3 |
||||||||||||||||||
1 |
Дана матрица A(4, 4) =((54, 81, 19, 43),(3, –44, 42, 51), (76, 5, 29, –24),(94, –92, –69, 28)). Найти сумму элементов по каждой из строк данного вектора |
197, 52, 86, –39 |
||||||||||||||||
2 |
Сформировать
матрицы А,
В,
С:,
и
выполнить
|
|
||||||||||||||||
3 |
Дан вектор А(10) ={1, –1, –3, 12, –10, –15, 7, 10, 1, 43}. Найти количество элементов в нем, значения которых больше среднего арифметического между максимальным и минимальным элементами |
2 |
||||||||||||||||
Продолжение табл. 5.1
1 |
2 |
3 |
||||||||||||||||
4 |
Дан вектор А(10) = (3, 17, –32, 45, –10, – 45, 67, 100, 56, 10}. Найти минимальный из положительных элементов данного вектора |
3 |
||||||||||||||||
5 |
Дана матрица A(4, 4) = ((54, 16, 96, 36), (10, –4, 23, 13), (74, 54, 24, –2), (94, –9, –6, 28)). Произвести транспонирование данной матрицы |
|
||||||||||||||||
Вариант 4
|
||||||||||||||||||
1 |
Найти
сумму элементов матрицы А = |
при L = 8: 15,1 |
||||||||||||||||
2 |
Сформировать
матрицы А,
В,
С:
|
|
||||||||||||||||
3 |
Дан вектор А(10) = (3, 17, –32, 45, –10, –45, 67, 100, 56, 10}. Найти максимальный из отрицательных элементов данного вектора |
–10 |
||||||||||||||||
4 |
В
матрице А
размерности 5 × 5:
|
121 |
||||||||||||||||
5 |
Дан вектор А(10) = {10, –17, –3, 5, –10, –5, 7, 10, 6, 1}. Поменять в этом векторе первый и последний элементы местами. |
(1, –17, –3, 5, –10, –5, 7, 10, 6, 10) |
||||||||||||||||
Вариант 5
|
||||||||||||||||||
1 |
Дана матрица A(4, 4)={{1, 8, 9, 3}, {3, –4, 2, 1}, {6, 5, 9, -4}, {9, –9, –9, 2}}. Найти сумму элементов, стоящих на главной диагонали данной матрице |
8 |
||||||||||||||||
Продолжение табл. 5.1
1 |
2 |
3 |
|||||||||||||||||||||||||
2 |
Сформировать
матрицы А,
В,
С:
и
выполнить
|
|
|||||||||||||||||||||||||
3 |
Дан вектор А(10)={1, –107, –23, 5, –120, –15, 17, 160, 66, 41}. Поменять местами первый и максимальный элементы данного вектора. |
(160, –107, –23, 5, –120, –15, 17, 1, 66, 41) |
|||||||||||||||||||||||||
4 |
Найти сумму квадратов положительных элементов матрицы А = |
552,01 |
|||||||||||||||||||||||||
5 |
Дан вектор А(10) = {10, –17, 3, 5, –10, –5, 7, 10, 6, 1}. Найти среднее арифметическое между максимальным и минимальным элементами данного вектора |
–3,5 |
|||||||||||||||||||||||||
Вариант 6 |
|||||||||||||||||||||||||||
1 |
В
матрице А
размерности 5×5:
|
29
|
|||||||||||||||||||||||||
2 |
Сформировать
матрицы А,
В,
С: |
|
|||||||||||||||||||||||||
3 |
Дан вектор А(10) = {10, –17, –3,5, –10, –5, 7, 10, 6, 1}. Найти сумму нечетных элементов данного вектора |
10 |
|||||||||||||||||||||||||
4 |
В
матрице А
размерности 5 × 5:
|
3,313 |
|||||||||||||||||||||||||
Продолжение табл. 5.1
1 |
2 |
3 |
||||||||||||||||
5 |
Дана матрица A(4, 4) = ((564, 816, 196, 436), (300, –44, 423, 513), (764, 554, 294, –24), (944, –92, –69, 284)). Поменять местами первую и вторую строчки данной матрицы |
|
||||||||||||||||
Вариант 7 |
||||||||||||||||||
1 |
Дана матрица A(4, 4) = ((4, 1, 9, 3), (3,–4, 2, 5), (6, 5, 9, –4), (9, –9, –6, 2)). Найти произведение элементов по каждому из столбцов данной матрицы |
648, 180, –972, –120 |
||||||||||||||||
2 |
Задать
матрицы А,
В,
С:
|
|
||||||||||||||||
3 |
Дан вектор А(10) = {10, –17, –3, 5, –10, –5, 7, 10, 6, 1}. Найти максимальный элемент в этом векторе и уменьшить все числа вектора на величину этого максимального элемента |
(0, –27, –13, –5, –20, –15, –3, 0, –4, –9) |
||||||||||||||||
4 |
В массиве поменять местами наибольший и наименьший элементы |
|
||||||||||||||||
5 |
Дан вектор А(10) = {10, –17, –3, 5, –10, –5, 7, 10, 6, 1}. Найти произведение четных элементов данного вектора |
4 250 |
||||||||||||||||
Вариант 8 |
||||||||||||||||||
1 |
Сформировать
матрицу B
размерности 4 × 4 следующим образом:
|
|
||||||||||||||||
2 |
Сформировать
матрицы А,
В,
С: |
|
||||||||||||||||
3 |
Дан вектор А(10) = {1, –1, –3, 5, –10, –5, 70, 10, 6, 1}. Найти количество элементов в данном векторе, абсолютное значение которых меньше 5 |
4 |
||||||||||||||||
4 |
Найти сумму квадратов отрицательных элементов матрицы А = |
6 858 |
||||||||||||||||
Продолжение табл. 5.1
1 |
2 |
3 |
||||||||||||||||
5 |
Дана матрица A(4, 4) = ((54, 81, 19, 43), (3, –44, 42, 51), (76, 5, 29, –24), (94, –92, –69, 28)). Найти минимальный элемент в каждом из ее столбцов |
19, –44, –24, –92 |
||||||||||||||||
Вариант 9 |
||||||||||||||||||
1 |
Сформировать
матрицу B
размерности 4 × 4 следующим образом:
|
|
||||||||||||||||
2 |
Сформировать матрицы А, В, С:
|
|
||||||||||||||||
3 |
Дан вектор А(10) = {34, 16, 12, –23, 41, –2, –67, 1, 8, –61}. Найти сумму отрицательных элементов данного вектора |
–153 |
||||||||||||||||
4 |
В матрице А размерности 5 × 5
|
16,567 |
||||||||||||||||
5 |
Дана матрица A (4, 4) = ((54, 81, 19, 43), (3, –44, 42, 51), (76, 5, 29, –24), (94, –92, –69, 28)). Найти максимальный элемент в данной матрице |
94 |
||||||||||||||||
Вариант 10 |
||||||||||||||||||
1 |
Сформировать
матрицу B
размерности 4 × 4 следующим образом:
|
|
||||||||||||||||
2 |
Сформировать
матрицы А,
В,
С:
|
|
||||||||||||||||
3 |
Дан вектор А(10) = {34, 16, 12, –23, 41, –2, –67, 1, 8, –61}. Найти сумму элементов, стоящих на четных местах в этом векторе |
–69 |
||||||||||||||||
Продолжение табл. 5.1
1 |
2 |
3 |
||||||||||||||||
4 |
Найти отношение максимального к минимальному по модулю элементу матрицы А = |
820 |
||||||||||||||||
5 |
Дана матрица A (4, 4) = ((54, 81, 19, 43), (3, –44, 42, 51), (76, 5, 29, –24), (94, –92, –69, 28)). Поменять местами первый и последний элементы каждого из столбцов данной матрицы |
|
||||||||||||||||
Вариант 11 |
||||||||||||||||||
1 |
Сформировать матрицу B размерности 4 × 4, используя матрицу A следующим образом:
A = |
|
||||||||||||||||
2 |
Сформировать
матрицы A,
B,
C:
|
|
||||||||||||||||
3 |
Упорядочить
по возрастанию компоненты вектора
А= |
(1, 2, 3, 4, 5, 6, 7, 8, 9,12) |
||||||||||||||||
4 |
Произвести транспонирование матрицы А размерности 4 × 4.
|
|
||||||||||||||||
5 |
Дана матрица A(4, 4) = ((564, 816, 196, 436), (300, –44, 423, 513), (764, 554, 294, –24), (944, –92, –69, 284)) Поменять местами последний столбец и столбец, где находится минимальный элемент данной матрицы |
|
||||||||||||||||
Продолжение табл. 5.1
1 |
2 |
3 |
||||||||||||||||
Вариант 12 |
||||||||||||||||||
1 |
Сформировать матрицу B размерности 4 × 4, используя матрицу A следующим образом:
|
|
||||||||||||||||
2 |
Сформировать
матрицы А,
В,
С:
|
|
||||||||||||||||
3 |
Упорядочить
по убыванию компоненты вектора А = |
(12, 9,8, 7, 6, 5, 4, 3, 2, 1) |
||||||||||||||||
4 |
В
матрице А
размерности 3 × 3: A= |
Сумма элементов по 1-й строке 57,2; по 2 –й — 6; по 3-й — 44,01; по 1-му столбцу — 24,00; по 2-му — 17,21; по 3-му — 66 |
||||||||||||||||
5 |
Дана матрица A(4, 4) = ((54, 81, 19, 43), (3, –44, 42, 51), (76, 5, 29, –24), (94, –92, –69, 28)). Поменять местами первый и последний элементы каждого из столбцов данной матрицы |
|
||||||||||||||||
Вариант 13 |
||||||||||||||||||
1 |
Сформировать
матрицу B
размерности 3 × 3, используя
матрицу A
следующим образом:
где
|
|
||||||||||||||||
2 |
Сформировать
матрицы А,
В,
С: и
вычислить
|
|
||||||||||||||||
Продолжить табл.5.1
1 |
2 |
3 |
||||||||||||||||
3 |
Произвести
перестановку элементов в обратном
порядке в массиве B
|
(34 –2.56 1 –1,34 -11,05 2,6 0,2 –0,31) |
||||||||||||||||
4 |
В
матрице А
размерности 3 × 4 A= |
Список нечетных элементов матрицы: A[1, 1] =1; A[1, 4] = 3; A[2, 2] = 7; A[2, 4] = 9; A[3, 1] = 7; A[3, 3] = 9; A[3, 4] = 13 |
||||||||||||||||
5 |
Дана матрица A(4, 4) = ((54, 81, 19, 43), (3, –44, 42, 51), (76, 5, 29, –24), (94, –92, –69, 28)). Найти в матрице максимальный элемент и уменьшить его на величину значения, находящегося на главной диагонали |
|
||||||||||||||||
Вариант 14 |
||||||||||||||||||
1 |
Сформировать
матрицу С:
c[i, j] = 1,
если i |
|
||||||||||||||||
2 |
Сформировать
матрицы А,
В,
С:
|
|
||||||||||||||||
3 |
Найти min и max по модулю элементы векторов A и B, где
|
0,230 –11 0,2 34 |
||||||||||||||||
4 |
В матрице А размерности 4×4 найти все четные элементы, вывести их и вычислить среднее арифметическое найденных элементов.
|
Четные элементы: 2,6,12,8,82,90 Среднее арифметическое 33,33 |
||||||||||||||||
5 |
Дана матрица A (4, 4) = ((54, 81, 19, 43), (3, –44, 42, 51), (76, 5, 29, –24), (94, –92, –69, 28)). Найти в матрице минимальный элемент и увеличить его на величину значения, находящегося на побочной диагонали |
|
||||||||||||||||
Продолжение табл. 5.1
1 |
2 |
3 |
||||||||||||||||
Вариант 15 |
||||||||||||||||||
1 |
Сформировать
матрицу С
=
A
+ B,
где
|
|
||||||||||||||||
2 |
Сформировать
матрицы A,
B,
C:
|
|
||||||||||||||||
3 |
Дан вектор А(10) = {10, –17, –3, 5, –10, –5, 7, 10, 6, 1}. Найти минимальный элемент в этом векторе и увеличить все числа вектора на величину этого минимального элемента |
(–7, –34, –20, –12, –27, –22, –10, –7, –11, –16) |
||||||||||||||||
4 |
Дана
матрица А
размерности 3 × 3: A
=
|
15,15 |
||||||||||||||||
5 |
Дана матрица A(4, 4) = ((54, 16, 96, 36), (10, –4, 23, 13), (74, 54, 24, –2), (94, –9, –6, 28)). Получить новую матрицу путем умножения максимального элемента из текущей на единичную матрицу |
|
||||||||||||||||

 заменить
знаки всех элементов противоположными
заменить
знаки всех элементов противоположными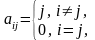
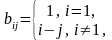

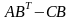
 и
выполнить
и
выполнить
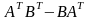
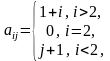
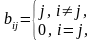
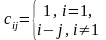
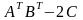
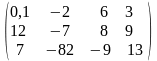 ,
не превышающих по модулю заданного
числа L
,
не превышающих по модулю заданного
числа L

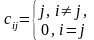 и
выполнить
и
выполнить
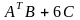
 найти сумму элементов, не делящихся
на 3 без остатка
найти сумму элементов, не делящихся
на 3 без остатка ,
,
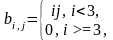
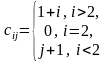

 найти сумму элементов главной диагонали
найти сумму элементов главной диагонали
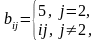
 и
выполнить
и
выполнить

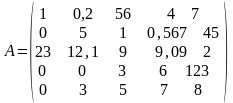 найти среднее арифметическое элементов
второстепенной диагонали
найти среднее арифметическое элементов
второстепенной диагонали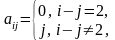

 и вычислить
и вычислить

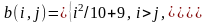
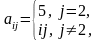

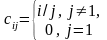 и
выполнить
и
выполнить
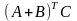

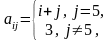

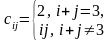 и
вычислить
и
вычислить
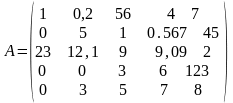 найти
сумму элементов второстепенной
диагонали
найти
сумму элементов второстепенной
диагонали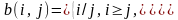
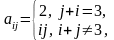

 и вычислить
и вычислить
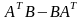

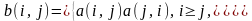

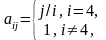
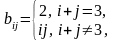
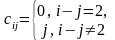 и вычислить
и вычислить
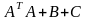

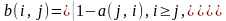 A =
A =
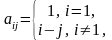
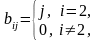
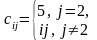 и
выполнить
и
выполнить
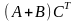
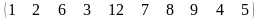
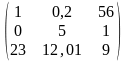 .
Найти сумму элементов в каждой строке
и в каждом столбце
.
Найти сумму элементов в каждой строке
и в каждом столбце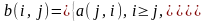

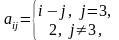
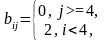
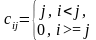

 .
.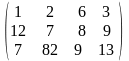 найти все нечетные элементы, вывести
их
найти все нечетные элементы, вывести
их j,
c[i, j] = 0,
если i
=
j
j,
c[i, j] = 0,
если i
=
j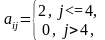
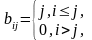
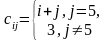 и вычислить
и вычислить

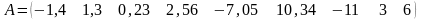 В =
В =
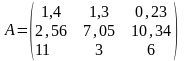 ,
,


 ,
,
 и вычислить
и вычислить

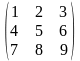 .
Найти сумму элементов по вторым строке
и столбцу. Дана матрица А
размерности 3 × 3: A =
.
Найти сумму элементов по вторым строке
и столбцу
.
Найти сумму элементов по вторым строке
и столбцу. Дана матрица А
размерности 3 × 3: A =
.
Найти сумму элементов по вторым строке
и столбцу