Излучение реальных тел

Абсолютно чёрное тело является идеализированным объектом по следующим двум причинам:

1. поверхность такого тела поглощает всю падающую энергию;

2. величина поглощения не зависит ни от длины волны излучения, ни от температуры.

Для любого реального тела эти условия выполняются с некоторой точностью. Поэтому энергетическая светимость реальных тел описывается законом Стефана-Больцмана тоже с некоторой точностью. Светимость реального тела, с учетом закона Кирхгофа, равна:

. (23)

Если поглощательная способность тела зависит только от длины волны и не зависит от температуры, т.е. 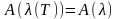, то даже в этом случае энергетическая светимость не пропорциональна четвёртой степени абсолютной температуры. Энергетическая светимость при условии, что коэффициент поглощения не зависит от длины волны, определяется выражением:

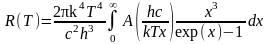. (24)

Зависимость интеграла от температуры возникает из-за зависимости поглощательной способности от длины волны. Таким образом, закон Стефана-Больцмана, 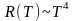выполняется как для абсолютно чёрного тела, так и для тела, у которого коэффициент поглощения не равен нулю и не зависит от длины волны:

. (25)

Такое тело называется серым. В этом случае светимость описывается формулой:

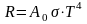. (26)

Экспериментальная установка

Установка для изучения закона Стефана-Больцмана для серого тела показана на рис. 5. Исследуется зависимость энергии, испускаемой спиралью нити накаливания, от ее температуры. Излучение от лампы накаливания (1) попадает на экранирующую трубку (2) с термоэлементом и усиливается усилителем (4). Ток, протекающий через нить лампы, измеряется амперметром (5). Напряжение на лампу подается от источника питания (3) и измеряется вольтметром (6). Усиленное напряжение от термоэлемента измеряется вольтметром (7). Для измерения сопротивления лампы при комнатной температуре используется сопротивление 100 Ω с соединительным «ящиком» (8).

Рис. 5. Экспериментальная установка для изучения закона Стефана-Больцмана: 1 — лампа накаливания; 2 — экранирующая трубка с термоэлементом; 3 — источник питания лампы; 4 — усилитель сигнала от термоэлемента; 5 — амперметр для измерения тока, протекающего через лампу; 6 — вольтметр для измерения напряжения на лампе; 7 — вольтметр для измерения усиленного сигнала от термоэлемента; 8 — сопротивление 100 Ω с соединительным «ящиком»

Методика эксперимента

Для определения температуры нити накаливания используется зависимость удельного сопротивления 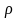материала (вольфрама), из которого эта нить сделана, от температуры:

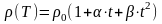, (27)

где ₀ — сопротивление при температуре 0 С, 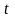— температура по шкале Цельсия. Коэффициенты  и  определяются из эксперимента и равны:

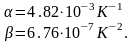(28)

Температура по шкале Цельсия t связана с температурой T по шкале Кельвина соотношением:

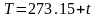. (29)

Сопротивление нити накаливания с площадью поперечного сечения S и длиной L равно:

. (30)

Зависимость сопротивления нити от температуры определяется выражением:

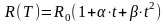. (31)

Если сопротивление R₀ при t = 0 °C известно, то выражение (31) позволяет определить температуру нити по известному сопротивлению:

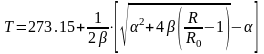. (32)

Сопротивление нити накаливания находится по закону Ома:

, (33)

где 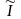— измеренный ток, 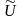— напряжение на лампе. Мощность W, выделяемая на нити накаливания, определяется законом Джоуля—Ленца:

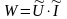. (34)

В установившемся режиме эта мощность должна отдаваться окружающей среде так, чтобы обеспечивать постоянную температуру нити накаливания. Поскольку нить не совершает работы, то условие баланса энергии можно записать в виде:

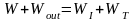. (35)

В этой формуле W — мощность энергии, выделяемая на нити накаливания при прохождении тока, W_out — мощность энергии, получаемая нитью от внешних источников, W_I — мощность, теряемая нитью за счёт излучения, W_T — мощность, отдаваемая нитью внешним телам за счёт теплообмена. Исследуем зависимость указанных мощностей от температуры:

• W_out: если нить излучает как серое тело, то:

, (35а)

где 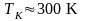— комнатная температура;

• W_I: для серого тела:

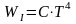, (35б)

где — температура нити, при которой проводятся измерения.

Большая разница комнатной температуры и температуры нити накаливания приводит к тому, что вкладом лучистой энергии от окружающих тел можно пренебречь:

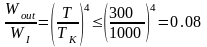. (35в)

• W_T: если теплообмен идёт по закону Ньютона, то:

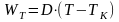. (35г)

При достаточно высоких температурах 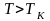тепловой баланс сводится к получению энергии от источника тока и излучению в соответствии с законом Стефана-Больцмана. Найдем отношение:

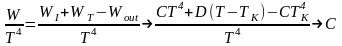. (36)

Таким образом, если отношение мощности, получаемой нитью, к четвёртой степени температуры перестаёт зависеть от величины тока, то это является весомым аргументом в пользу того, что нить излучает как серое тело.