Полигон частот

С оединим точки x_i и n_i и получим ломанную или полигон частот.

Средняя арифметическая вариационного ряда

Средней арифметической вариационного ряда называется дробь, числитель которой- сумма произведений вариант ряда , а знаменатель- объем выборки или соответствующие им веса.

Пример: Вычислить среднее число обрывов нити на станке за время t.

Кол-во обрывов	Кол-во промежутков
0 1 2 3 4 5 6 7 8	31 157 214 253 151 111 57 17 6	0 157 428 759 604 555 342 119 48
Итого: 36	1000	3012

Теорема: Если варианты увеличить или уменьшить в одно и тоже число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз.

;

Пример 2.

Приведено распределение по заработной плате. Вычислить среднюю з/п рабочих цеха №1.

З/плата, руб.	Число рабочих цеха			Всего
	цех№1	цех№2	цех№3
70-80 80-90 90-100 100-110 110-120 120-130	7 12 15 6 - -	1 5 9 18 12 5	- - 4 8 32 16	8 17 28 32 44 21
Итого:	40	50	60	150

Средняя з/плата	Цех№1
75 85 95 105 115 125	7 12 15 6 - -	525 1020 1425 630 - -
Итого:	40	3600

;

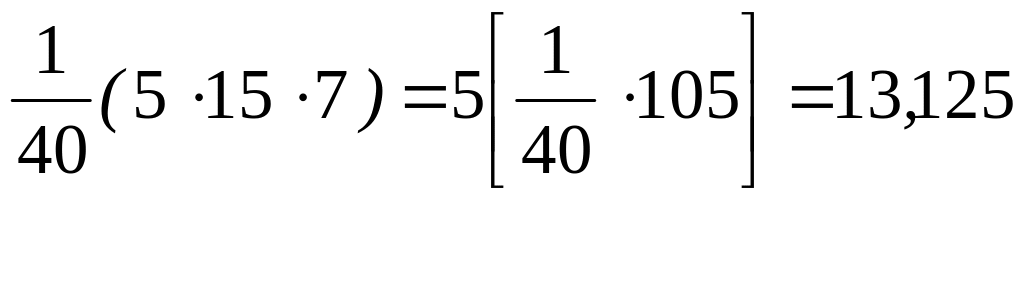
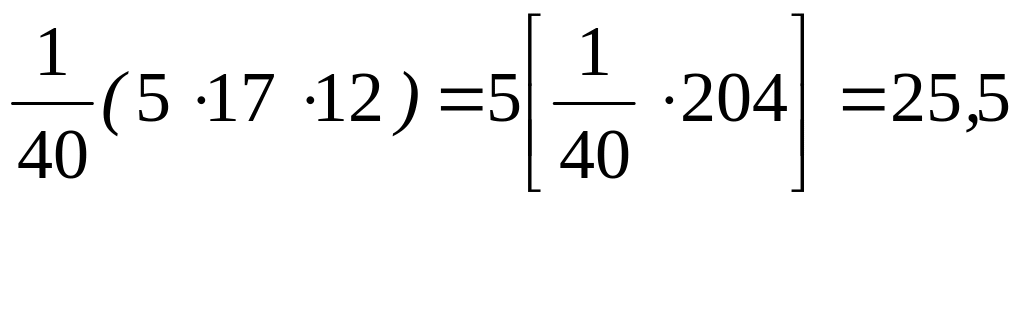
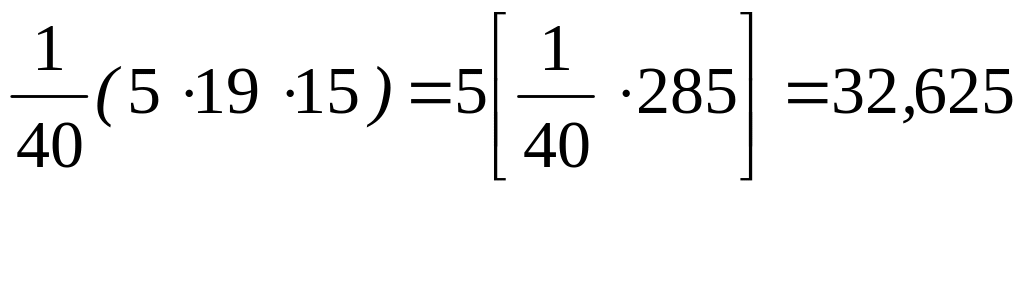
	ni	ni
15 17 19 21	7 12 15 6	105 204 285 126
Итого:	40

Теорема №2: Если варианты уменьшить или увеличить на одно и тоже число раз, то средняя арифметическая уменьшится на то же число раз.

;

Пример: Вычислить среднюю з/плату рабочих цеха№2 ,применяя теорему №2.

xi	xi-c	Ni
75 85 95 105 115 125	-30 -20 -10 0 10 20	1 5 9 18 12 5	-30 -100 -90 0 120 100

c- берем равное 105 , что соответствует варианту с наибольшей частотой.

Теорема №3.

Сумма произведений отклонений вариантов от средней арифметической на соответствующие веса равна 0.

.

Теорема №4.

При увеличении или уменьшении весов в одно и тоже число раз, средняя арифметическая не меняется.

;

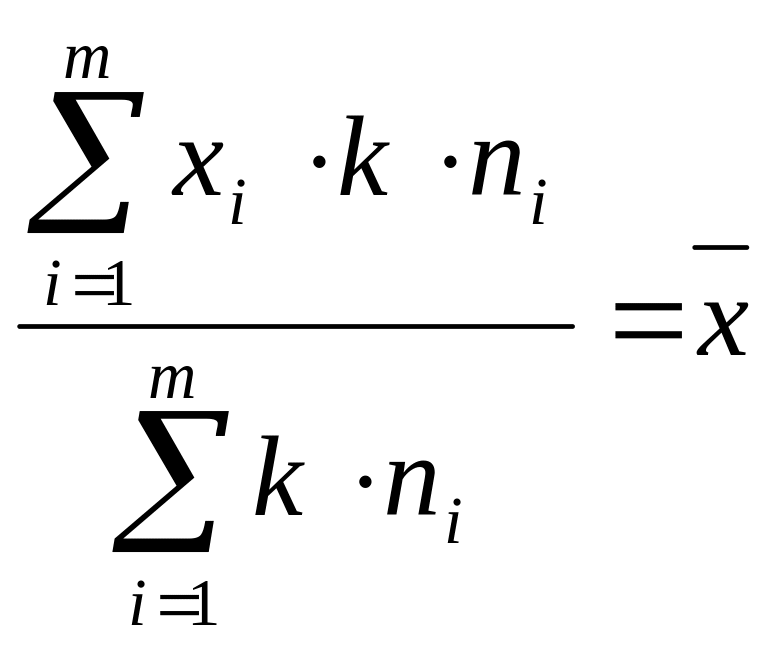Используя эту теорему, вычислим среднюю з/п цеха №3.

З/плата	цех№3	ni/4	ni/4k
75 85 95 105 115 125	- - 4 8 32 16	- - 1 2 8 4	- - 4 16 256 64
Итого:	60		340

; k=4.

Пусть некоторая совокупность разбита на группы не обязательно одинаковые по объему, тогда среднюю арифметическую распределения членов группы называют групповыми средними, а средние арифметические распределения по тому же признаку всей совокупности - общей средней. Группы называются непересекающимися, если каждый член совокупности принадлежит только одной группе.

Пусть распределение признака s в s - непересекающихся группах S₁,S₂,…S_n и по всей совокупности s представлены в таблице:

xi	S1	S2	…..	Sl	S
x1	P1	q1	…..	r1	P1+q1+…+r1=n1
x2	P2	q2	…..	r2	P2+q2+…+r2=n2
…..	…..	…..	…..	…..	…..
xm	Pm	qm	…..	rm	Pm+qm+…+rm=nm
Итого:	N1	N2	…..	Nml

; ; ;

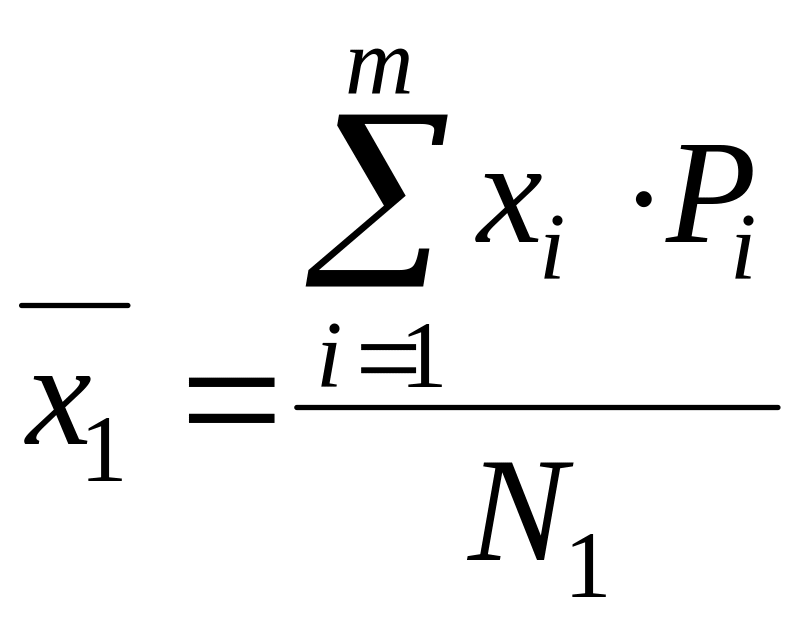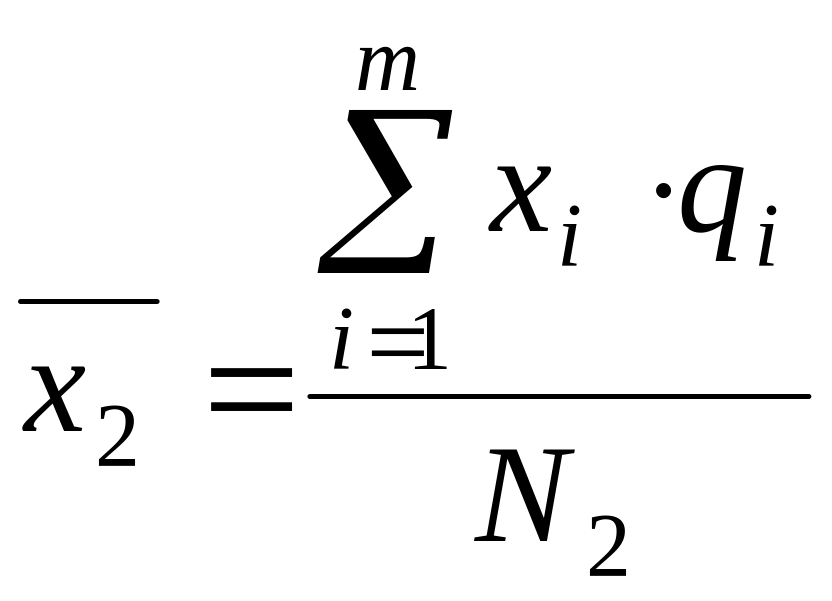Общая средняя того же признака :

;

Сгруппируем

;

Теорема №5

Общая средняя равна средней арифметической групповых средних всех непересекающихся групп.

Пример: Вычислить среднюю з/плату рабочих всего предприятия.

;

;

Теорема №6

Если каждое значение признака z представляет сумму или разность значений x и y, то средняя арифметическая признака z равна сумме или разности средних арифметических x и y.

;