Содержание
1. Тема – Предел функции |
4 |
2. Тема – Производная функции |
10 |
3. Тема – Исследование графика функции |
14 |
4. Тема – Неопределенный интеграл |
16 |
5. Тема – Определенный интеграл |
22 |
6. Тема – Приложения определенного интеграла |
26 |
7. Тема – Несобственные интегралы |
30 |
8. Литература |
33 |
Тема – предел функции
Определение.
Число
называется пределом значений функции
,
,
в точке
,
если для любой последовательности точек
такой, что
последовательность
значений функции
в точках
имеет своим пределом число
,
в этом случае
пишут 
.
Приведенное
определение включает и особые случаи,
когда числа
и
будут заменены символами
и
:
,
,
и т.д.
Одним из важнейших
результатов является равенство
,
которое носит название первого
замечательного предела.
А. Вычислить пределы :
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
B. Вычислить пределы :
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
C. Вычислить пределы, используя первый замечательный предел :
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
D. Вычислить пределы, используя правило Лопиталя :
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
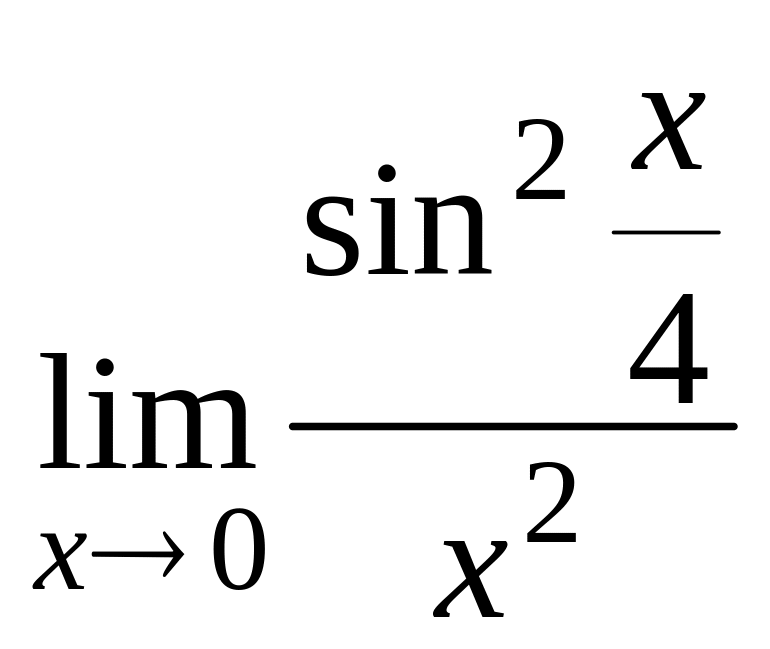
тема – Производная функции
Определение.
Производной функции
в точке
называется
предел отношения приращения функции
к вызвавшему его приращению аргумента
,
при стремлении приращения аргумента
к нулю :
Если этот предел
конечный, то функция
называется дифференцируемой в точке
; при этом она оказывается обязательно
и непрерывной в этой точке. Если же
предел равен
или
,
то будем говорить, что функция
имеет в точке
бесконечную производную, однако при
дополнительном условии, что функция в
этой точке непрерывна.
Производная
обозначается
,
или
,
или
,
или
.
Нахождение производной называется
дифференцированием функции.
A. Найти производные от функций :
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
B. Найти производные от функций :
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
C. Найти производные от сложных функций :
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
тема - исследование графика функции
Определение.
Функция
имеет экстремум ( максимум или минимум
) в точке
,
если
является наибольшим или наименьшим
значением функции в некоторой двусторонней
окрестности этой точки.
Необходимое
условие существования экстремума.
Функция
имеет экстремум в точке
,
если первая производная функции
в этой точке равна нулю
или не существует.
Достаточные условия существования экстремума. Если функция непрерывна в точке и имеет в некоторой окрестности кроме, может быть, самой точки , конечную производную и если при переходе через :
меняет свой знак с + на -, то точка - точка максимума ;
меняет свой знак с - на +, то точка - точка минимума ;
не меняет знака, то экстремума нет.