14. Виды ошибок выборочного наблюдения.

Ошибоки репрезентативности, которые представляют собой разность между обобщающими показателями генеральной выборочной совокупностей.

Ошибки репрезентативности могут быть рассчитаны как средняя или стандартная (μ) и максимальная с определенной вероятностью – предельная ( ).

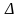Средняя ошибка выборки для собственно случайного и механического способа.

При повторном методе отбора .

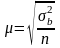При бесповторном методе отбора ,

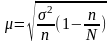где 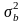- дисперсия выборочных данных; n – объем выборки; N – объем генеральной совокупности.

Средняя ошибка типического отбора.

При повторном методе отбора .

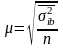При бесповторном методе отбора ,

где 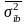- средняя из групповых вариаций в выборке по типическим группам.

Средняя ошибка при отборе сериями (серийная выборка).

При повторном отборе .

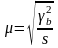При бесповторном отборе ,

где - межгрупповая вариация; s – количество отобранных серий; S – количество серий в генеральной совокупности.

Предельная ошибка выборки ( ) связана со средней ошибкой и коэффициентом доверия (t)

.

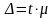15. Форма взаимосвязи социально-экономических явлений

Различают два вида связей, существующих между явлениями, – функциональные и стохастические.

Функциональной называется зависимость, при которой одному значению факторного признака строго соответствует единственное значение результативного признака.

Стохастическая зависимость характеризуется тем, что результативный признак неполностью определяется факторным признаком, его влияние проявляется в среднем при достаточно большом числе наблюдений.

Наиболее часто для исследования стохастических зависимостей используют метод корреляции.

Термин корреляция происходит от английского слова correlation – соотношение, соответствие.

К изучению связи методом корреляции обращаются в том случае, когда нельзя изолировать влияние посторонних факторов. При этом число наблюдений должно быть достаточно велико, так как малое число наблюдений не позволяет обнаружить закономерность связи.

Первая задача корреляции заключается в математическом выражении изменения результативного признака в связи с изменением одного или несколько факторных признаков. Данная задача решается определением уравнения регрессии и носит название регрессионного анализа. Вторая задача состоит в определении степени влияния искажающих факторов –различных показателей тесноты связи и называется корреляционным анализом.

Регрессионный анализ включает в себя этапы:

1. Логический анализ – разделение коррелирующих признаков на факторные и результативный.

2. Определение типа зависимости. Корреляционная зависимость называется парной, если она имеет место между двумя признаками (факторным и результативным) и множественной (многофакторной) – между тремя и более связанными между собой признаками.

16. Методы оценки тесноты связи в кореляционных зависимостях.

Для оценки тесноты связи в статистическом анализе используют показатели:

эмпирического корреляционного отношения (η_э)

,

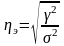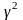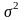где - межгрупповая вариация результативного признака; - общая вариация результативного признака.

Наличие взаимосвязей между результативным и факторным признаком имеет при η ≤ 0,5.

Универсальным показателем тесноты связи является показатель теоретического корреляционного отношения или индекс корреляции (η_m)

,

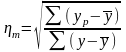где 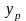- рассчитанные (теоретические) значения результативного признака.

Показатель теоретического корреляционного отношения может использоваться для оценки тесноты связи не только в парных, но и многофакторных зависимостей.

Для оценки тесноты связи прямолинейной зависимости используется линейный коэффициент корреляции (r)

или

.

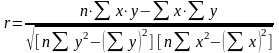Линейный коэффициент корреляции может изменяться от -1 до +1. Чем ближе значение r по абсолютной величине к единице, тем теснее связь. Если r>0, то связь между факторным и результативным признаками прямо пропорциональная, если r<0, то обратно пропорциональная.

Для предварительной оценки тесноты связи корреляции может использоваться коэффициент корреляции знаков (коэффициент Г. Фехнера).

Для определения коэффициента знаков Г. Фехнера вычисляются средние значения факторного и результативного признаков, затем определяются знаки отклонений от средней всех значений взаимосвязанных признаков. Приняв число совпадений знаков отклонений индивидуальных значений от средней за «С», а число несовпадений за «Н», коэффициент определяется следующим образом:

.

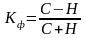Коэффициент Г. Фехнера может принимать значения от -1 до +1; если он положительный, то связь между признаками признается прямой, если отрицательный, то обратной.

Рассмотренные выше показатели корреляции приемлемы лишь для условий нормального или близкого к нормальному распределения и только для количественных признаков. Если эти условия отсутствуют и к тому же исследуются атрибутивные признаки, то приходится пользоваться непараметрическими методами корреляционного анализа, в частности корреляцией рангов или ранговой корреляцией. Ранг признака (R_i) указывает то место, которое занимает i-й признак среди других n-признаков в ранжированном ряду распределения.

Если одно и то же значение признака в ранжированном ряду распределения занимает разные порядковые номера, то ранг признака определяется по сопряженному рангу (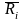 ), рассчитанному как среднее арифметическое порядковых номеров, занимаемых данным признаком.

Для такого рода ранжированных признаков показателями тесноты связи служат коэффициенты корреляции рангов К. Спирмэна (ρ) и М. Кендэла (τ).

,

где n – число сопоставимых пар; d – разность между рангами коррелирующих признаков ( ).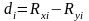

Этот коэффициент интерпретируется также, как и линейный коэффициент корреляции, имеет те же свойства и пределы значений (от -1 до +1)

,

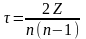где Z – алгебраическая сумма числа высших (P) и низших (Q) рангов по отношению к каждому последующему рангу y, сопоставленному в строгом соответствии с рядом значений х в восходящем или нисходящем порядках, т.е. Z=P-Q.

Расчет данного коэффициента выполняется в следующем порядке:

1. Значения признака х выстраиваются в строчной последовательности возрастания или убывания.

2. Значения у располагаются в порядке, соответствующем значениям х.

3. Для каждого ранга у определяется число следующих за ним значений рангов, превышающих его величину. Суммируя эти числа определяется величина Р как мера соответствия последовательностей рангов х и у.

4. Для каждого ранга у определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина этих чисел обозначается Q.

Как правило, коэффициент М. Кендэла меньше коэффициента Спирмэна

.

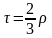Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) 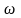, который вычисляется по формуле

,

где m – количество факторов; S – отклонение суммы квадратов рангов от средней квадратов рангов

.

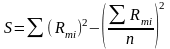Связь между признаками признается значимой, если значение коэффициентов корреляции рангов больше 0,5.

Теснота связей между атрибутивными признаками с большим числом вариантов измеряется с помощью коэффициентов сопряженности К. Пирсона (К_n) или А. Чупрова (К_r)

,

,

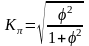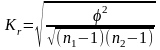где n₁ – число вариантов признака по горизонтали; n₂ – число вариантов признака по вертикали; φ² – показатель взаимной сопряженности

,

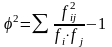где 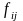- частота внутри клетки таблицы; 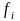- итоговая частота по строке; - итоговая частота по графе.

Коэффициент сопряженности А. Чупрова считается более точным показателем по сравнению с показателем К. Пирсона, так как учитывает число образованных по признакам групп.