Практична робота №7

Тема: Алгоритм Дейкстри

Мета:

1. Опанувати особливості конкретного середовища програмування.

2. Опанувати методику створення програмного продукту.

3. Реалізувати алгоритм Дейкстри.

Теоретичні відомості

Алгоритм Дейкстри вирішує задачу про найкоротший шлях із однієї вихідної вершини для зваженого орієнтованого графа з вихідною вершиною , в якому ваги всіх ребер невід’ємні ( ) для всіх .

Формальне пояснення

В процесі роботи алгоритму Дейкстри підтримується множина , яка складається із вершин , для яких вже знайдено. Алгоритм вибирає вершину із найменшим , додає до множини і виконує полегшення всіх ребер, які виходять із , після чого цикл повторюється. Вершини, які не лежать в , зберігаються в черзі 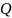з пріоритетами, які визначаються значеннями функції . Передбачається, що граф заданий за допомогою списків суміжних вершин.

Неформальне пояснення

Кожній вершині із 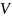співставимо мітку – мінімально відома відстань від цієї вершини до 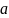. Алгоритм працює покроково – на кожному кроці він "відвідує" одну вершину і намагається зменшити мітки. Робота алгоритму завершується, коли всі вершини відідані.

Ініціалізація. Мітка самої вершини ставиться рівною , мітки інших вершин – нескінченності. Це відображає те, що відстані від до інших вершин поки невідомі. Всі вершини графа помічаються як невідвідані.

Крок алгоритму. Якщо всі вершини відвідані, алгоритм завершується. В іншому випадку із ще не відвіданих вершин вибирається вершина , яка має мінімальну мітку. Ми розглядаємо всі можливі маршрути, в яких є передостаннім пунктом. Вершини, з’єднані з вершиною ребрами, назвемо сусідами цієї вершини. Для кожного сусіда розглянемо нову лінію шляху, яка дорівнює сумі поточної мітки і довжини ребра, яке з’єднує із цим сусідом. Якщо отримана довжина менше мітки сусіда, замінимо мітку цією довжиною. Розглянувши всіх сусідів, помітимо вершину як відвідану і повторимо крок.

Приклад

Розглянемо роботу алгоритму на прикладі графа, який наведений на рис. 1. Нехай потрібно знайти відстані від 1-ї вершини до всіх інших.

Рис. 1

Кружками позначені вершини, лініями – шляхи між ними (ребра графа). В кружках позначені номера вершин, над ребрами позначена їх ціна – довжина шляху. Поруч з кожною вершиною червоним позначена мітка – довжина найкоротшого шляху в цю вершину із вершини 1 (рис. 2).

Рис. 2

Перший крок. Розглянемо крок алгоритму Дейкстри для нашого прикладу. Мінімальну мітку має вершина 1. Її сусідами є вершини 2, 3 і 6 (рис. 3).

Рис. 3

Перший в черзі сусід вершини 1 – вершина 2, тому що довжина шляху до неї мінімальна. Довжина шляху до неї через вершину 1 дорівнює найкоротшому шляху до вершини 1 + довжина ребра, яке йде із 1 в 2, тобто, 0+7. Це менше поточної мітки вершини 2, тому нова мітка 2-ї вершини дорівнює 7 (рис. 4).

Рис. 4

Аналогічно операція виконується з двома іншими сусідами 1-ї вершини – 3-ю та 5-ю (рис. 5-6).

Рис. 5

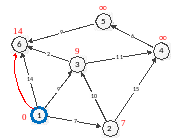
Рис. 6

Всі сусіди вершини 1 перевірені. Поточна мінімальна відстань до вершини 1 вважається остаточною і перегляду не підлягає (те, що це дійсно так, вперше довів Дейкстра). Викреслимо її із графа, щоб відмітити, що ця вершина відвідана (рис. 7).

Рис. 7

Другий крок. Крок алгоритму повторюється. Знову знаходимо найближчу і не відвіданих вершин. Це вершина 2 із міткою 7 (рис. 8).

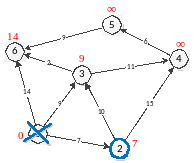
Рис. 8

Знову намагаємось зменшити мітки сусідів обраної вершини, намагаючись знайти пройти в них через 2-гу. Сусідами вершини 2 є 1, 3, 4.

Першим (по порядку) сусідом вершини 2 є вершина 1. Але вона вже відвідана, тому із 1-ю вершиною нічого не робимо.

Наступний сусід вершини 2 – вершина 4. Якщо йти до неї через 2-гу вершину, то довжина такого шляху буде = найкоротша відстань до 2 + відстань між вершинами 2 і 4 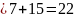. Оскільки , то встановлюємо мітку вершини 4 рівною 22 (рис. 9).

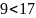Ще один сусід вершини 2 – вершина 3. Якщо іти до неї через 2, то довжина такого шляху буде . Але поточна мітка вершини 3 дорівнює , тому мітка не змінюється (рис. 10).

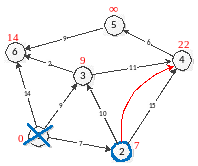
Рис. 9

Рис. 10

Всі сусіди вершини 2 переглянуті, залишаємо відстані до неї і помічаємо її як відвідану.

Третій крок. Повторюємо крок алгоритму, вибравши вершину 3.

Подальші кроки. Повторюємо крок алгоритму для вершин, що залишилися (це будуть по порядку 6, 4 і 5).

Завершення виконання алгоритму. Алгоритм завершує свою роботу, коли відвідані всі вершини. Результат його роботи: найкоротший шлях від вершини 1 до: 2 складає 7, до 3 – 9, до 4 – 20, до 5 – 20, до 6 – 11.