Формулы алгебры логики

Всякое сложное высказывание может быть записано через элементарные высказывания с использованием логических операций. Такое выражение называется формулой алгебры логики. Обозначаются формулы большими латинскими буквами. Для упрощения записи применяют ряд условий: скобки можно не ставить, учитывая, что операции выполняются в следующем порядке – конъюнкция, дизъюнкция, импликация, эквивалентность. ( )

Пример, Составить таблицу истинности для формулы А=

х	y
0	1	1	1	1
0	1	1	0	0
1	0	0	0	1
1	1	0	1	1

Формула алгебры логики называют выполнимой, если на наборах входящих в нее переменные принимают значение 0 и 1.

Формулу алгебры логики называют истинной, если на наборах входящих в нее переменные принимают значение «1» и ложной, если принимают значение «0».

Равносильные формулы алгебры логики. Две формулы алгебры логики А и В называются равносильными, если на наборах входящих в нее переменные принимают одинаковые значения

Теорема. Если две формулы алгебры логики А и В равносильны, то истиной является их эквивалентность и наоборот, если эквивалентность – истинна, то формулы равносильны.

Группы равносильностей

1.Основные равносильности:

2. Группа выражающая основные логические операции через другие логические операции:

Из второй группы равносильности видно, что любые формулы алгебры логики можно записать, используя лишь конъюнкцию и отрицание или дизъюнкцию и отрицание.

3. Группа, выражающая основные законы алгебры логики:

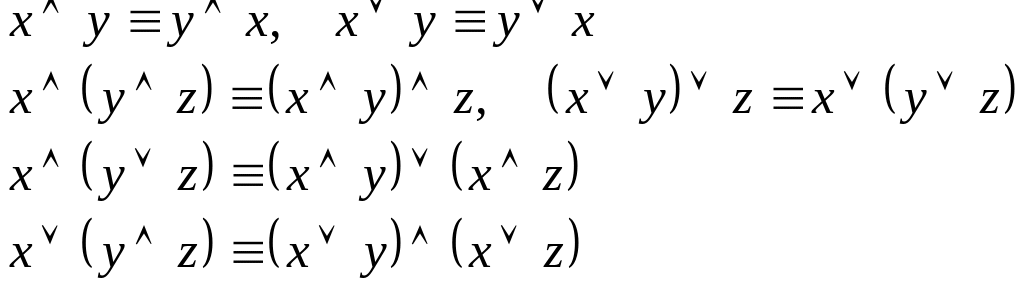
Коммутативные законы

Ассоциативные законы

Дистрибутивность конъюнкции относительно дизъюнкции

Дистрибутивность конъюнкции относительно дизъюнкции

Равносильные преобразования формул.

Равносильные преобразования формул используют для доказательств равносильности и приведения формул к более простому виду. Формула А считается проще равносильной ей формуле В, если в ней операции импликации и эквивалентности заменены на конъюнкцию, дизъюнкцию и отрицание, а отрицание относительно лишь к элементарному высказыванию. Равносильность обозначается « »

Закон двойственности

Операция конъюнкция является двойственной для дизъюнкции, а дизъюнкция – двойственной для конъюнкции.

Формула А называется двойственной для формулы В, если все входящие в нее операции заменены на двойственные. Если формулы А и В равносильны, то равносильны и их двойственные формулы.

Алгебра Жегалкина

Это алгебра, в которой определены две логические операции: сложение по модулю «два» и конъюнкция.

Справедливы следующие соотношения:

Чтобы записать полином Жегалкина для произвольной формулы алгебры логики нужно все входящие в нее операции заменить на сложение по модулю «два» и конъюнкцию, используя при этом равносильности:

Совершенная дизъюнктивная нормальная форма (СДНФ)

Элементарной конъюнкцией n-переменных называется конъюнкция этих переменных или их отрицаний.

Дизъюнктивной нормальной формой (ДНФ) для формулы А называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.

Для любой формулы алгебры логики можно получить ДНФ, при чем не единственную.

Свойства совершенства

1. Каждое слагаемое, входящее в формулу, содержит все переменные входящие в исходную формулу.

2. Все слагаемые в формуле различны.

3. Ни одно слагаемое не содержит одновременно переменную и ее отрицание.

4. Ни одно слагаемое не содержит одну и ту же переменную дважды.

ДНФ для которой выполняются формулы совершенства называют совершенной ДНФ (СДНФ).

Пути нахождения СДНФ:

1. Находим любую ДНФ.

2. Если какое-то слагаемое не содержит всех переменных (например х), то к слагаемому дописываем 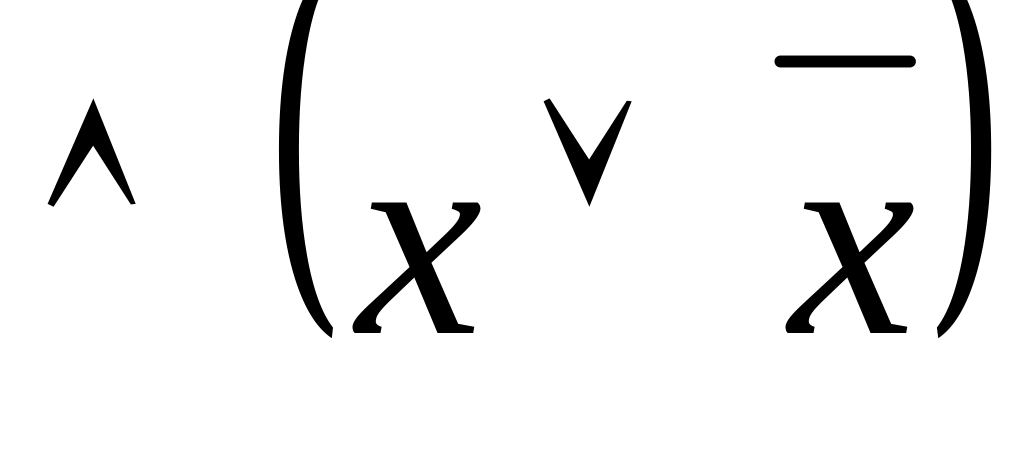и пользуемся свойством

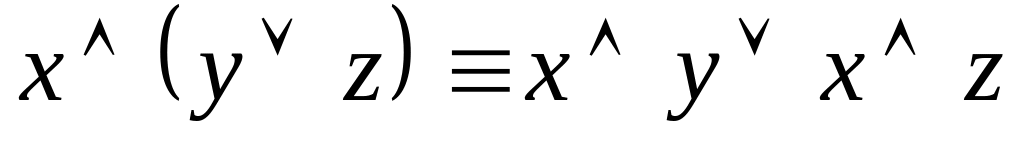
3. Если слагаемое содержит переменную и ее отрицание, то оно обращается в «0».

4. Если формула содержит 2 одинаковых слагаемых, то по свойству 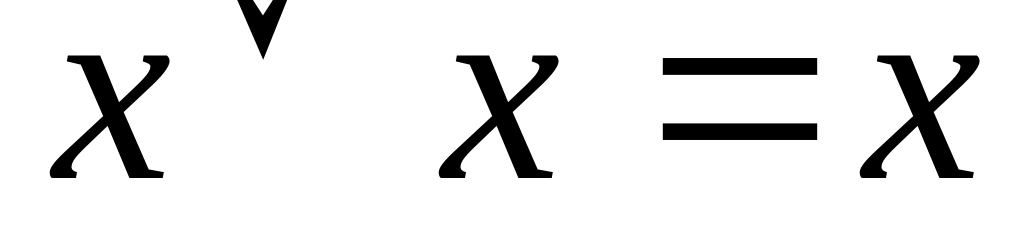остается одно слагаемое.

5. Если формула содержит два одинаковых элемента, то по свойству 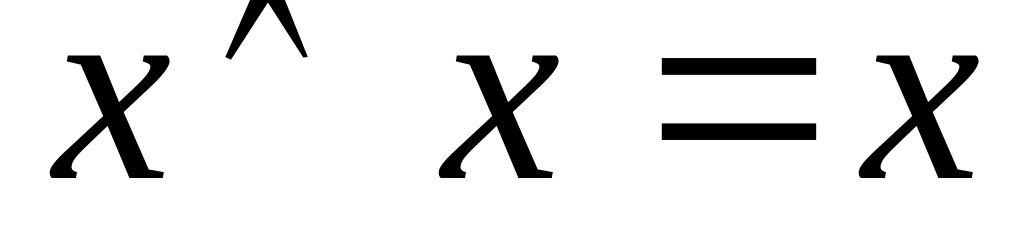остается один элемент.