МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ВТ

отчет

по лабораторной работе №5

по дисциплине «Информатика»

Тема: Решение уравнений и систем уравнений в Matlab.

Студентка гр. 9494		Лобазев Н.А.
Преподаватель		Гречухин М.Н.

Санкт-Петербург

2019

Оглавление

Цель работы 2

Основные теоретические положения 3

Вывод 11

Цель работы

Научиться решать уравнения и системы линейных уравнений в Matlab.

Требования и рекомендации к выполнению задания:

Нумерация вариантов соответствует номеру студенческого билета. При этом 9-й билет решает 1 вариант, 10й – 2й вариант, 11й – 3й и так далее.

1. Решить уравнение задана в таблице 4.1.

2. Решить систему уравнений, заданную в таблице 4.2 методом обратной матрицы, Крамера и Гаусса. Вывести на экран все три результата и убедиться, что они совпадают.

Основные теоретические положения

1. Решение уравнений вида

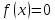
Для нахождения корней многочлена в Matlab используется функция roots. Полином задаётся в виде вектора коэффициентов при степенях 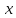, т. е. имеет вид .

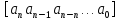2. Решение систем линейных уравнений

Система линейных алгебраических уравнений в самом общем случае имеет вид:

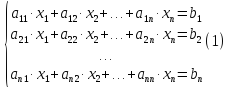
Для вычислений в Matlab удобно представлять такую систему в виде матрицы коэффициентов и вектора свободных членов :

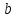Тогда систему (1) можно записать в виде:

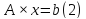
где – вектор-столбец неизвестных.

Метод обратной матрицы.

Если 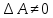, то тогда система (1) имеет единственное решение, которое выражается как

Таким образом, нам необходимо посчитать обратную матрицу для матрицы коэффициентов и перемножить её со столбцом свободных членов.

Метод Крамера.

Суть метода Крамера состоит в следующем. Если для представления системы уравнений (1.1) соблюдается условие , то система имеет единственное решение следующего вида:

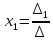
и т. д., где

т. е. определитель матрицы А (1.1), в которой 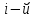столбец заменён столбцом свободных членов .

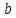Метод Гаусса.

Метод Гаусса предполагает проведение преобразований с так называемой расширенной матрицей системы уравнений, т. е. с матрицей вида 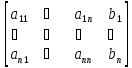с целью приведения её к виду . Последний столбец будет содержать значения неизвестных. Система будет иметь единственное решение, когда

В Matlab для решения систем уравнений методом Гаусса используется встроенная функция rref.

Ход работы.

Решение уравнений вида

Задание 1

f=[1 -15 78 -178 177 63]

f =

1 -15 78 -178 177 63

>> roots(f)

ans =

6.7223 + 0.0000i

4.9844 + 0.0000i

1.7827 + 1.9317i

1.7827 - 1.9317i

-0.2721 + 0.0000i

>>

Решение систем линейных уравнений

1. Метод обратной матрицы.

A=[3 -3 -1 5 -3; -1 3 4 0 -1; 3 5 3 4 3; 3 -2 -4 1 4; -1 2 4 -4 3]

A =

3 -3 -1 5 -3

-1 3 4 0 -1

3 5 3 4 3

3 -2 -4 1 4

-1 2 4 -4 3

>> b=[-2; 0; -5; -4; -4]

b =

-2

0

-5

-4

-4

>> x=inv(A)*b

x =

15.4000

8.8000

-5.4000

-11.8000

-10.6000

2.Метод Крамера.

A=[3 -3 -1 5 -3; -1 3 4 0 -1; 3 5 3 4 3; 3 -2 -4 1 4; -1 2 4 -4 3]

A =

3 -3 -1 5 -3

-1 3 4 0 -1

3 5 3 4 3

3 -2 -4 1 4

-1 2 4 -4 3

>> b=[-2; 0; -5; -4; -4]

b =

-2

0

-5

-4

-4

>> rank(A)

ans =

5

>> A1 = A

A1 =

3 -3 -1 5 -3

-1 3 4 0 -1

3 5 3 4 3

3 -2 -4 1 4

-1 2 4 -4 3

>> A2 = A

A2 =

3 -3 -1 5 -3

-1 3 4 0 -1

3 5 3 4 3

3 -2 -4 1 4

-1 2 4 -4 3

>> A3 = A

A3 =

3 -3 -1 5 -3

-1 3 4 0 -1

3 5 3 4 3

3 -2 -4 1 4

-1 2 4 -4 3

>> A4 = A

A4 =

3 -3 -1 5 -3

-1 3 4 0 -1

3 5 3 4 3

3 -2 -4 1 4

-1 2 4 -4 3

>> A5 = A

A5 =

3 -3 -1 5 -3

-1 3 4 0 -1

3 5 3 4 3

3 -2 -4 1 4

-1 2 4 -4 3

>> A1(:,1) = b

A1 =

-2 -3 -1 5 -3

0 3 4 0 -1

-5 5 3 4 3

-4 -2 -4 1 4

-4 2 4 -4 3

>> A2(:,2) = b

A2 =

3 -2 -1 5 -3

-1 0 4 0 -1

3 -5 3 4 3

3 -4 -4 1 4

-1 -4 4 -4 3

>> A3(:,3) = b

A3 =

3 -3 -2 5 -3

-1 3 0 0 -1

3 5 -5 4 3

3 -2 -4 1 4

-1 2 -4 -4 3

>> A4(:,4) = b

A4 =

3 -3 -1 -2 -3

-1 3 4 0 -1

3 5 3 -5 3

3 -2 -4 -4 4

-1 2 4 -4 3

>> A5(:,5) = b

A5 =

3 -3 -1 5 -2

-1 3 4 0 0

3 5 3 4 -5

3 -2 -4 1 -4

-1 2 4 -4 -4

>> x1 = det(A1) / det(A)

x1 =

15.4000

>> x2 = det(A2) / det(A)

x2 =

8.8000

>> x3 = det(A3) / det(A)

x3 =

-5.4000

>> x4 = det(A4) / det(A)

x4 =

-11.8000

>> x5 = det(A5) / det(A)

x5 =

-10.6000

>> x=[x1;x2;x3;x4;x5]

x =

15.4000

8.8000

-5.4000

-11.8000

-10.6000

3.Метод Гаусса.

A=[3 -3 -1 5 -3; -1 3 4 0 -1; 3 5 3 4 3; 3 -2 -4 1 4; -1 2 4 -4 3]

A =

3 -3 -1 5 -3

-1 3 4 0 -1

3 5 3 4 3

3 -2 -4 1 4

-1 2 4 -4 3

>> b=[-2; 0; -5; -4; -4]

b =

-2

0

-5

-4

-4

>> C = [A b]

C =

3 -3 -1 5 -3 -2

-1 3 4 0 -1 0

3 5 3 4 3 -5

3 -2 -4 1 4 -4

-1 2 4 -4 3 -4

>> D = rref(C)

D =

1.0000 0 0 0 0 15.4000

0 1.0000 0 0 0 8.8000

0 0 1.0000 0 0 -5.4000

0 0 0 1.0000 0 -11.8000

0 0 0 0 1.0000 -10.6000

>> x = D(:,6)

x =

15.4000

8.8000

-5.4000

-11.8000

-10.6000

Вывод

Я научился решать уравнения и системы уравнений в Matlab. По ходу работы у меня получилось так, что всеми 3 способами решения систем уравнений вышли одинаковые ответы, получается, что я все сделал правильно.