
- •Лекция №1. Основные понятия.
- •Лекция №2.
- •3 Вида схем:
- •Лекция №3. Математическое описание сау.
- •Лекция №4. Типовые звенья сау.
- •Лекция №5. Переходная и весовая функции.
- •Лекция №6. Основные характеристики типовых звеньев сау
- •Лекция 7 Передаточные функции разомкнутых и замкнутых систем
- •Лекция 8 Точность сау
- •Лекция №9. Устойчивость сар
- •Лекция №10 Критерий Гурвица (критерий асимптотической устойчивости)
- •Лекция №11 Критерий устойчивости Михайлова
- •Лекция №12 Критерий устойчивости Найквиста
- •Лекция №13 Качество сар в переходных процессах
- •Лекция №14 Корректирующие устройства
- •Лекция №15 Параллельные корректирующие устройства.
- •Лекция №16. Корректирующие устройства по внешнему воздействию.
- •Лекция №17. Метод корневого годографа.
Лекция №5. Переходная и весовая функции.
h(t) – переходная функция - реакция системы на единичное воздействие.

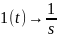 ;
;
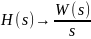 ;
;
 ;
;

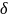 (t)
– весовая функция - реакция системы на
единичный импульс.
(t)
– весовая функция - реакция системы на
единичный импульс.


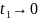 ;
;
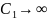 ;
;
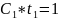 ;
;
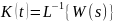 ;
;
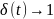 ;
;
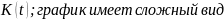
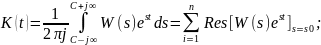
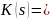
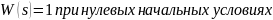
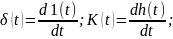
По весовой функции можно определить передаточную функцию системы, и наоборот.
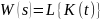
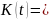
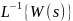 ;
;
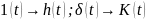
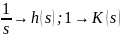
Частотные характеристики САУ

Частотные характеристики – формулы, графики, характеризующие реакцию САУ на гармоническое входное воздействие при установившемся режиме.
А – усиление амплитуды.
Символическая форма записи гармонического сигнала:
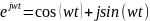
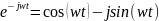
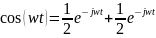
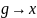
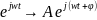
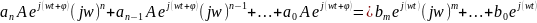
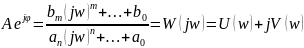
W(jw) – амплитудно-фазовая частотная характеристика (АФЧХ)
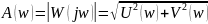 – амплитудно-частотная
характеристика (АЧХ).
– амплитудно-частотная
характеристика (АЧХ).
►АЧХ определяет коэффициент усиления входного гармонического сигнала при его прохождении через систему.

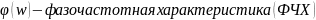
►ФЧХ показывает сдвиг фазы входного гармонического сигнала по отношению ко входному сигналу.

В реальных системах сдвиг фаз отрицательный.
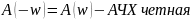
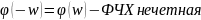

Сплошная
линия –
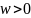
Пунктирная
–
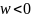
W(s) – дробно-рациональная функция.
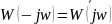
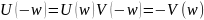
►Логарифмическая частотная характеристика (ЛЧХ).
Частота может изменяться в широких пределах, поэтому характеристики считают в логарифмическом масштабе.
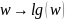
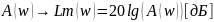

Между частотными характеристиками и весовой функцией существует отношение: s = jw
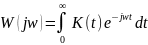
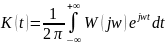
Эти соотношения называются прямым и обратным преобразованием Фурье.
Лекция №6. Основные характеристики типовых звеньев сау
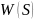


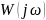

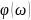
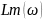
1)Безынерционное звено:
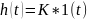 -
весовая функция
-
весовая функция
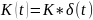
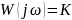 -
АФЧХ
-
АФЧХ
 -
АЧХ
-
АЧХ
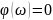 -
ФЧХ
-
ФЧХ
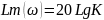 – ЛАЧХ
– ЛАЧХ




2) Идеальное дифференцирующее звено:
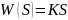
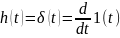
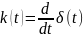
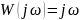
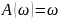
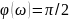
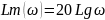



3)Идеальное интегрирующее звено:
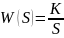
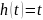
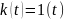
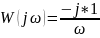
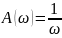
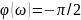
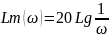





4)Дифференцирующее звено 1 порядка:
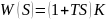
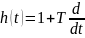
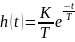
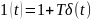
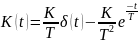
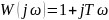
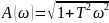
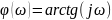
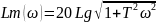
Асимптоты:
При
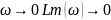
При
![]()
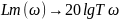




5)Апериодическое звено:
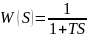
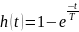
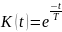
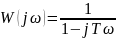
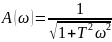
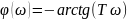
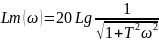
Асимптоты:
При
При
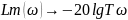





6)Колебательное звено:
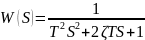
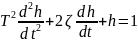
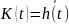
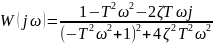
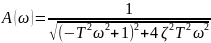
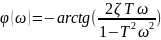
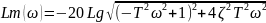
Асимптоты:
При
При
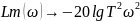




Лекция 7 Передаточные функции разомкнутых и замкнутых систем
Передаточная функция разомкнутой системы (Рис. 7.1):

Рис. 7.1
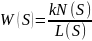
Примечание: звено называется интегрирующим, если в знаменателе есть в чистом виде S; если S в чистом виде находится в числителе, то звено называется дифференцирующим.
Дифференциальное уравнение системы в форме L:
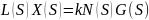
Передаточная функция системы при последовательном соединении звеньев (см. Рис. 7.2):


Рис. 7.2
Передаточная функция системы при параллельном соединении звеньев (см. Рис. 7.3):
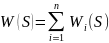

Рис. 7.3
Местная обратная связь:
Уравнение системы с обратной связью (см. Рис. 7.4):

Рис. 7.4
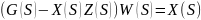
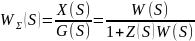
При единичной обратной связи:
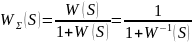
Примечание: далее W(S)-передаточная функция разомкнутой системы, Ф(S)-передаточная функция замкнутой системы. Передаточная функция замкнутой системы:
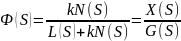
Характеристический полином замкнутой системы:
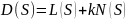
Характеристическое уравнение замкнутой системы:
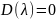
Характеристическое уравнение разомкнутой системы:
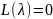
Передаточная функция по возмущающему воздействию:
Рассмотрим систему, изображенную на рис. 7.5.

Рис. 7.5
Примечание:
g(t)/G(S)-управляющее воздействие
х(t)/Х(S)-регулируемая величина
f(t)/F(S)-возмущающее воздействие
ε(t)/ ε (S)-ошибка
Функция
ошибки:
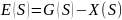
Передаточная функция по ошибке:
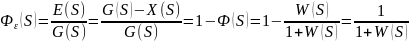
Преобразуем исходную схему с помощью правил структурных преобразований (см. Рис. 7.6) :

Рис. 7.6
Следовательно:
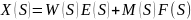

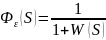
Значит, передаточная функция по возмущающему воздействию равна:
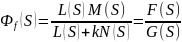
Примечание: порядок разомкнутой системы определяется по порядку замкнутой системы.
Основные уравнения следящих систем.
Дифференциальное уравнение системы (см. Рис.7.6):
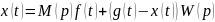
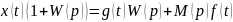
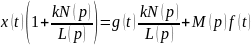
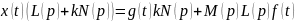
Обозначим:
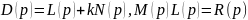
Дифференциальное уравнение замкнутой системы:
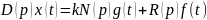
Дифференциальное уравнение по отклонению по ошибке:
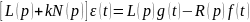
Дифференциальное уравнение системы в форме Коши при отсутствии возмущающих и входных воздействий:
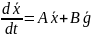
Данное уравнение определяет собственное движение системы
Характеристическое уравнение для данного ДУ:
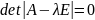 ,
где Е - единичная матрица
,
где Е - единичная матрица
