Признак единственности решения злп, найденного симплекс методом.

Если оценки всех свободных векторов-столбцов не равны нулю, найденное оптимальное решение единственно.

4) Если оптимальное решение не найдено, ищем новое опорное решение.

Признак отсутствия оптимального решения в силу неограниченности целевой функции.

ЗЛП не имеет решения в силу неограниченности целевой функции, если какой-нибудь столбец коэффициентов свободной переменной, оценка которого противоречит признаку оптимальности, не содержит ни одного положительного элемента.

Если условие отсутствия оптимального решения не выполняется, введём в базис новую переменную, столбец коэффициентов которой имеет оценку, противоречащую признаку оптимальности. Если таких столбцов несколько, выбираем столбец с «наихудшей» оценкой.

Для выбора разрешающего элемента в столбце новой базисной переменной используем условие неотрицательности свободных членов. Из базиса выводится столбец с разрешающим элементом (единицей) в соответствующей строке.

Получив новое опорное решение, вычисляем соответствующее ему значение целевой функции.

Приращение целевой функции при переходе от одного опорного решения к другому можно вычислить по формуле:

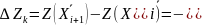
Тема 6. Основы теории двойственности.

Правило построения задачи, двойственной к данной.

1.) Если целевая функция одной задачи в паре стремится к минимуму, то целевая функция другой задачи стремится к максимуму.

2) Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений в другой.

3) Количество переменных в двойственной задаче равно числу ограничений в исходной.

4)Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.

5) Задача на максимум – все ограничения с . В задаче на минимум – все ограничения с .

6) Если в системе ограничений задачи k-е ограничение является равенством, то на k-ю переменную в двойственной задаче не накладывается условие неотрицательности.

Первая теорема двойственности:

Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение. Причём значения целевых функций этих задач на своих оптимальных решениях совпадают.

Оптимальное решение одной из задач можно найти из решения симплекс методом другой задачи, прибавив к оценкам разложений по базису оптимального решения векторов, входящих в начальный базис начального решения соответствующие коэффициенты целевой функции.

Если одна из пары двойственных задач не имеет решения ввиду неограниченности целевой функции, то другая не имеет решения ввиду несовместности системы ограничений.

Вторая теорема двойственности:

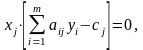
Допустимые решения и являются оптимальными решениями пары двойственных задач тогда и только тогда, когда и

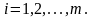
Вопросы к модулю, отжатые у менеджеров. Вам вполне подходят.

I. Элементы матанализа нескольких переменных.

1) Понятие частного приращения и частной производной.

2) Предел и непрерывность функции нескольких переменных

3) Примеры функций нескольких переменных

4) Понятие вектора градиента функции

5) Экстремум функции. Определение и необходимое условие.

6) Матрица Гессе. Достаточные условия экстремума.

II. Постановка задачи математического программирования.

1) Общий вид ЗМП.

2) Понятие операции, целевой функции и системы ограничений.

3) Что такое допустимое и что такое оптимальное решение ЗМП.

4) Как привести систему к стандартному виду.

5) Как привести систему к каноническому виду.

6) Общий вид ЗЛП.

III. Метод Лагранжа решения ЗМП.

1) Способ построения функции Лагранжа.

2) Поиск точек возможного экстремума функции Лагранжа.

3) Матрица Гессе ЗМП с двумя переменными и одним ограничением.

4) Экономический смысл множителей Лагранжа.

IV. Графический метод решения ЗЛП.

1) Общий вид линейной задачи программирования с двумя неизвестными.

2) Принцип построения ОДР.

3) Анализ количества решений ЗЛП графическим методом (с картинками)

4) Поиск оптимального решения на ОДР.

V. Симплекс метод решения ЗЛП.

1) Основания для применения.

2) Поиск начального решения.

3) Условие неотрицательности. Параметр тетта.

4) Вычисление оценок.

5) Критерии оптимальности и единственности.

6) Критерий отсутствия (существования) оптимального решения.

7) Как изменить базисное решение? Как при этом меняется значение целевой функции?

VII. Основы теории двойственности.

1) Правила составления двойственных задач.

2) Первая теорема двойственности

3) Вторая теорема двойственности.