Тема 5. Симплекс метод.

Симплекс метод – это метод целенаправленного перебора опорных решений задачи линейного программирования (ЗЛП).

Основания для применения симплекс метода:

1) ОДР ЗЛП – выпуклое множество с конечным числом угловых точек;

2) оптимальное решение ЗЛП – это одна из угловых точек ОДР;

3) угловые точки ОДР – базисные решения (опорные планы) системы ограничений.

Базисные решения – допустимые решения вида , содержащие r базисных и n-r свободных переменных.

Все свободные переменные равны нулю, а базисные переменные равны соответствующим свободным членам в преобразованной (разрешённой относительно базисных переменных) системе ограничений.

Чтобы решения системы уравнений ограничений были допустимыми, должно выполняться

условие неотрицательности свободных членов:

При любых преобразованиях уравнений системы ограничений, свободные члены уравнений должны оставаться неотрицательными.

Чтобы выполнить это условие, в процессе преобразований системы методом Жордано-Гаусса, выбираем разрешающий элемент в k-ом столбце только после вычисления вспомогательного параметра :

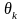= , здесь r- номер строки, в которой находится разрешающий элемент k-ого столбца.

[делим каждый свободный член на каждый элемент k-ого столбца, выбираем наименьшее отношение и по его местоположению определяем строку k-ого столбца, содержащую разрешающий элемент ]

Алгоритм применения симплекс – метода.

1) Приводим ЗЛП к каноническому виду.

2) Находим начальное опорное решение.

[составляем симплекс таблицу,

преобразуем расширенную матрицу уравнений ограничений методом Жордано – Гаусса, разрешаем её относительно m базисных переменных, выбранных произвольно, но с соблюдением условия неотрицательности,

приравниваем свободные переменные к нулю, вычисляем значения базисных переменных,

находим значение целевой функции для найденного начального опорного решения].

3) Проверяем найденное опорное решение на оптимальность.

[ заполняем первые два столбца симплекс таблицы,

вычисляем оценки векторов столбцов коэффициентов при свободных переменных (см. ниже),

проверяем выполнение признаков оптимальности и единственности найденного решения:

если все оценки столбцов свободных переменных положительны, найден максимум ЗЛП,

если все оценки столбцов свободных переменных отрицательны, найден минимум ЗЛП,

если хотя бы одна из оценок столбцов свободных переменных равна нулю, решений бесконечно много, они находятся по формуле , где 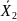находим путём перебора всех опорных решений ЗЛП].

Вычисление оценки разложения вектора условий по базису опорного решения.

или ,

где - вектор – столбец коэффициентов целевой функции при базисных переменных, - вектор – столбец коэффициентов системы ограничений при k-ой переменной, - коэффициент в целевой функции при k-ой переменной.

Признаки оптимальности решения злп, найденного симплекс методом.

Допустимое решение ЗЛП на максимум является оптимальным,

если оценки всех векторов столбцов коэффициентов неотрицательны.

[ЗЛП на максимум - ].

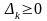Допустимое решение ЗЛП на минимум является оптимальным, если оценки всех векторов столбцов коэффициентов не положительны [ЗЛП на минимум - ].

Оценки всех базисных столбцов равны 0.