1. Чуть чуть из матанализа функции нескольких переменных.

Частные и полные приращения функции двух переменных.

- полное приращение;

и - частные приращения.

Частные производные функции двух переменных.

Частной производной по х от функции называется производная, вычисленная в предположении, что у – постоянная. (производная по у вычисляется при постоянной х)

;

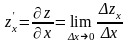Частными производными второго порядка функции называются частные производные от её частных производных первого порядка.

1) = = = 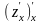; 2) = = =

Смешанные производные: 3)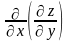 = = = 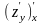; 4) = = =

Если смешанные производные непрерывной функции двух переменных непрерывны, то они равны между собой. =

Определение локального экстремума функции двух переменных.

Функция имеет локальный максимум (минимум) в точке М₀(х₀,у₀), если значении функции в этой точке больше (меньше), чем её значение в любой другой точке М(х,у) некоторой окрестности точки М_0.

(точка. М₀ – максимум, если для любых точек её окрестности.)

(Точка М₀ – минимум, если для любых точек её окрестности.)

Условия существования экстремума для функции двух переменных.

Необходимое: Если функция достигает экстремума при х=х₀, у=у₀, то каждая частная производная первого порядка от этой функции при этих значениях аргументов или обращается в ноль или не существует.

Достаточное: Пусть в некоторой окрестности точки М₀(х₀,у₀) функция имеет непрерывные частные производные, равные нулю в этой точке, тогда, если , М₀(х₀,у₀) – является экстремумом функции ,

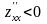причём, если , точка М₀ – минимум, если , точка М₀ – максимум.

Вектор градиент. Вектор, координаты которого равны частным производным функции , называется вектором градиентом этой функции. .

Вектор градиент показывает направление максимального возрастания значения функции.

2. Постановка задачи математического программирования (мп).

Операция – управляемое мероприятие, направленное на достижение цели.

Условие задачи математического программирования состоит из:

(1) = - целевой функции, характеризующей зависимость

результата операций от её факторов, переменных ЗМП.

(2) системы ограничений, состоящей из m равенств

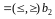или неравенств, показывающих

… связи между факторами операции.,

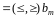
Допустимым решением ЗМП называют любой n-мерный вектор 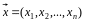, удовлетворяющий системе ограничений (2) и естественному условию неотрицательности переменных

Совокупность всех допустимых решений образуют область в n-мерном пространстве – ОДР.

Решить ЗМП – выбрать из всех допустимых решений то, при котором результат операции будет наилучшим (целевая функция (1) достигнет своего наибольшего или наименьшего значения).

Оптимальным решением ЗМП называется допустимое решение ЗМП, при котором целевая функция = достигает экстремума.