3)Система обслуживания с m серверами явными потерями: m/m/m/Loss
Система без образования очереди для заявок, поступивших в моменты, когда все m серверов были заняты. Такие заявки будут просто теряться. В телефонии это типичный случай коммутирования на конечном коммутационном поле. Опишем такую систему подходящим процессом типа гибели-размножения. Его параметры могут быть определены так
Такая система оказывается также эргодичной и диаграмма интенсивностей переходов, приведенная на рис. 3
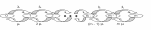
Рис. 3 Диаграмма интенсивностей переходов для СМО типа M/M/m:Loss.
Основной характеристикой QoS для этой системы является средняя доля времени, когда все серверы оказываются занятыми. В этом случае говорят о том, что в системе наступила блокировка.
4)Система типа m/m/m:m
Систему, имеющую одинаковое число входных линий и обслуживающих серверов, например выходных линий. Очевидно, что блокировка в такой системе невозможна. Диаграмма интенсивностей переходов состояний может быть представлена в виде совокупности несвязных m простейших подсистем с двумя состояниями – свободно/занято. ( Рис. 1.20)
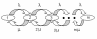
Рис. 1.20 Диаграмма интенсивностей переходов состояний для СМО типа M/M/m:m.
Вероятности того, что k подсистем находятся в состоянии «занято», описывается формулой Энгсета:
.
Нетрудно видеть, что в этом случае в знаменателе записан бином Ньютона, и формула для вероятностей может быть существенно упрощена:
Полученное распределение вероятностей носит название биноминального или распределения Бернулли. Величина a определяет вероятность занятости сервера, а величина (1-a) – вероятность его простоя. Поскольку таких серверов m , то распределение вероятностей будет таким же, как для классической задачи о бросании m монет. Следует отметить также что
5) Вероятность занятия серверов
Нам необходимо найти вероятность занятия определенных, выбранных заранее серверов. Эта задача часто встречается при определении нагрузки на определенные выходы в коммутаторах каналов телефонных сетей. В результате применения модели Эрланга или Энгсета или Бернулли найдены вероятности занятия любых k серверов pk .
Зафиксируем
определенные i
серверов из m
доступных.
Предположим, что занятие серверов
происходит равновероятно. Тогда если
в системе с вероятностью
занято
точно i
+ j
серверов, то вероятность занятия одной
конкретной комбинации будет в число
таких сочетаний раз меньше, т.е.
.
Поскольку отмеченные i серверов могут быть заняты совместно с любыми другими j серверами в соответствующем числу сочетаний из m по j комбинациях, где j любое число от 0 до m-i , то можно получить формулу для вероятности занятия фиксированных i серверов в системе с M входами:
.
Для модели Эрланга тогда получим:
.
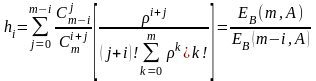Для модели Энгсета формула будет отличаться:
.
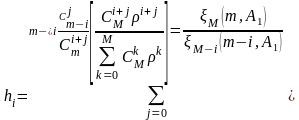Для системы с одинаковым числом входов и выходов (серверов) имеет место модель Бернулли и соответствующие вероятности занятия фиксированных серверов будут:
.
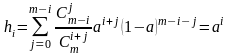