1. Коэффициент использования линии (сервера), единичное приращение интенсивности обслуженной нагрузки

Коэффициента использования линии (сервера):

.

---------------------------------------------------------------------------------------------------------------------

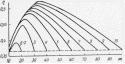
Рис. 1. Среднее использование линии  в НВ в зависимости от емкости пучка m при различных значениях g, D=10 и P=0.003.

---------------------------------------------------------------------------------------------------------------------

Важной характеристикой СМО с несколькими серверами является единичное приращение интенсивности обслуженной нагрузки при увеличении числа серверов на единицу и постоянной норме потерь - вероятности блокировки. Эту величину называют единичным приращением:

.

---------------------------------------------------------------------------------------------------------------------

Это неравенство говорит о том, что удвоение числа серверов увеличивает пропускную способность системы более чем вдвое.

---------------------------------------------------------------------------------------------------------------------

Рис. 2 Зависимость единичного приращения y_ от числа выходов m при обслуживании простейшего потока и различных вероятностях потерь Р_В.

Формула О’Делла:

Где, число серверов m, доступностью D, обслуженной нагрузке Y

---------------------------------------------------------------------------------------------------------------------

Коэффициент использования сервера при γ =1:

.

---------------------------------------------------------------------------------------------------------------------

Формулу Пальма -Якобеуса для определения обслуженной нагрузки и вероятности блокировки:

2. Модели интеграции речи и данных

Рассмотрим объединение двух видов нагрузки – обслуживание с коммутацией каналов, кратко – речь и нагрузка, требующая обслуживания с коммутацией пакетов – данные.

Назовем первую из этих видов нагрузка 1-го класса. Будем считать, что интенсивность поступлений ВЫЗОВОВ (требований на соединение) λ₁ а среднее время занятия 1/μ₁. Этот тип нагрузки требует одного временного канала и при отсутствии свободных каналов – блокируется.

Второй из видов нагрузки назовем Нагрузка 2-го класса. Интенсивность поступлений ПАКЕТОВ положим равной λ₂, а средняя длина пакета определяет время обслуживания 1/μ₂. Эта группа заявок ставится в очередь при отсутствии свободных каналов. В этом и состоит основное отличие двух классов нагрузки с точки зрения теории телетрафика.

Для обслуживания нагрузки в зависимости от класса может быть выделено фиксированное или переменное число каналов. В зависимости от способа предоставления каналов для заявок разного класса будет получаться различное качество обслуживания нагрузки.

3. Задача. К компьютерной системе поступают три типа задач:

А) диалоговые задачи

Б) испытательные задачи

В) производительные задачи

Все задачи прибывают согласно Пауссонвскому процессу, и времена обслуживания являются постоянными.

Интенсивность поступления задач следующая:

А) 18 задач прибывают в минуту, и время обслуживания -5 с

Б) 7 задач прибывают в минуту, и время обслуживания -10 с

В) 14 задач прибывают в час, и время обслуживания – 2 минуты

Найдите предложенную нагрузку для каждого типа и полную предложенную нагрузку.

Решение:

А) 18*5/60 = 1,5

Б) 7*10/60 = 1,17

В) 14*120/3600 = 0,47

1,5+1,17+0,47 = 3,14 – полная предложенная нагрузка

20. Билет