БИЛЕТ №1

1. Анализ систем массового обслуживания с Марковскими потоками требований. Система М/M/1.  Это система с пуассоновским входным потоком заявок, экспоненциальным законом распределения времени обслуживания и одним сервером.

Рис. 1.10 СМО типа М/М/1.

«гибели-размножения».

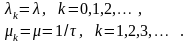
Здесь  – среднее время обслуживания в сервере.

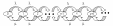
Рис. 1.11 Диаграмма интенсивности переходов для СМО типа М/М/1.

Полученное ранее общее решение позволяет сразу записать вероятность того, что в стационарном состоянии в очереди будет находиться k заявок

Окончательно получаем формулу для вероятности длины очереди

.

Рис. 1.12 Стационарные вероятности рк для СМО типа М/М/1.

Важной характеристикой системы является средняя длина очереди. Зная вероятности каждого из возможных значений длины, найдем математическое ожидание:

.

Найдем теперь дисперсию длины очереди: .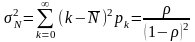

Для нахождения среднего значения времени пребывания в очереди воспользуемся формулой Литтла.

.

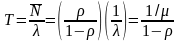2. Теорема Джексона.

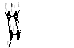
Рис. 1 Сеть, содержащая N узлов.

Должно выполняться условие баланса

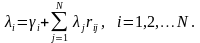
Вероятность, того, что заявка после обслуживания в i-том узле вообще покинет сеть будет равна .

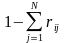Джексону удалось доказать, что стационарная вероятность этого состояния разлагается в произведение безусловных распределений:

.

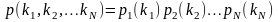Которые представляют собой стационарные вероятности для классической системы M/M/m. Этот удивительный результат называют теоремой Джексона.

Пусть в замкнутой сети с тремя (N=3) узлами циркулирует ровно два требования (K=2).

Состояние сети описывается тройками: .

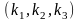Всего в сети возможно различных состояний .

На рис. 3 показана диаграмма интенсивностей переходов между этими состояниями.

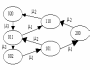
Рис. 3 Диаграмма интенсивностей переходов для замкнутой сети с тремя узлами.

3. Задача.

Расмотрим интернет–кафе. Клиенты прибывают случайно, в среднем 20 клиентов в час. Среднее время использования терминала – 15 минут. Найдите предложенную нагрузку, измеренную в единицах среднего времени обслуживания в течения одного часа. Найдите предложенную нагрузку, измеренную в Эрлангах

Лямда=20 кл

А=лямда*t=20*3600=72000

7200/900=80 Эрл

Билет 2

1) Системы с неполнодоступным включением серверов

Системы с несколькими серверами могут по-разному распределять их ресурс для обслуживания поступающих заявок. Если за определенными серверами закрепляются заявки, поступающие только с определенных входных линий, то говорят о неполнодоступном включении серверов (НВ).

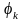- функцию состояния k, значение которой равно вероятности обслуживания заявки, поступившей в СМО в этом состоянии. Стационарное распределение вероятностей в этом случае будет зависеть как от параметра входного потока, так и от значения .

Диаграмма интенсивностей переходов для СМО с m серверами, явными потерями и неполнодоступным включением изображена на рисунке 1:

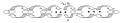
В общем случае в неполнодоступной схеме выделяют нагрузочные группы - полнодоступные коммутационные системы, обеспечивающие подключение любого из n-входов к D-выходам, и объединительную схему, представляющую собой набор сумматоров в аналоговой схемотехнике или набор логических «или» в цифровой. В старых АТС объединительная схема реализуется в виде простых «монтажных или» в промежуточном щите переключений (ПЩ).

Рис. 2 Система с неполнодоступным включением.

2) Анализ систем массового обслуживания без явных потерь. Марковские системы, в которых каждая заявка проходила только одну операцию обслуживания, такие системы можно назвать однофазными. Если заявка получает обслуживание более чем в одном сервере, то говорят о многофазных.

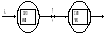
Рис. 1 Простейшая последовательная система с двумя узлами

Обозначим ее преобразование Лапласа

.

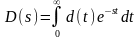Преобразование Лапласа плотности вероятности промежутка времени между заявками для случая пустого узла 1 будет:

.

Здесь B(s) – преобразование Лапласа плотности вероятности времени обслуживания.

Поскольку время обслуживания является случайной величиной с показательным законом распределения, то:

.

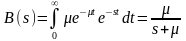Используя то свойство, что вероятность того, что заявка покинет систему пустой, равна вероятности того, что заявка поступит в момент, когда в системе нет заявок и равна в точности 1-ρ. Это позволяет записать преобразование Лапласа для плотности вероятности распределения промежутка времени полностью в виде