1. Метод суммирования значений всех показателей

Оценка R_i каждого подразделения i определяется по формуле:

Данным методом пользуются в случае одинаковой направленности исходных показателей и их общей сопоставимости (например, все показатели выражены в процентах выполнения плана). Наилучшее подразделение определяется по максимальной сумме показателей-стимуляторов и по минимальной сумме показателей-дестимуляторов.

Таким образом, критерий оценки наилучшего подразделения для показателей-стимуляторов – max R_i (1 ≤ i ≤ п), а для показателей-дестимуляторов – min R_i (1 ≤ i ≤ п).

2. Метод суммы мест

По исходным данным (по матрице X и вектору S) строится вспомогательная матрица Р по следующим правилам:

а) при s_i = +1 элементы столбца j матрицы X упорядочиваются по убыванию и элементу р_ij придается значение, соответствующее месту элемента х_ij среди упорядоченных элементов j-го столбца;

б) при s_i = -1 элементы столбца j матрицы X упорядочиваются по возрастанию и элементу р_ij придается значение, соответствующее месту элемента х_ij среди упорядоченных элементов j-го столбца.

Таким образом, по каждому j-му показателю объекты упорядочиваются по значениям этого показателя. Оценка R_i каждого подразделения i вычисляется по формуле:

Критерий оценки наилучшего подразделения: min R_i (1 ≤ i ≤ п).

3. Метод суммы баллов

При построении балльных оценок, кроме исходных данных о значениях показателей, задаются шкалы для оценки каждого показателя. Наиболее распространенными являются непрерывные и дискретные шкалы. Они характеризуются минимальным и максимальным количеством баллов, которыми может быть оценен показатель. Верхняя и нижняя границы шкалы могут иметь как положительное, так и отрицательное значение, то есть оценки могут быть и положительными, и отрицательными. Так, показатели выполнения плана по выпуску продукции, себестоимости могут оцениваться положительной и отрицательной величинами, а, например, показатели травматизма - только отрицательными величинами.

Дискретная шкала задает определенное число уровней оценок (баллов), с помощью которых оценивается показатель. Как правило, в этом случае выбираются целочисленные балльные оценки. Например, показатель производительности труда может оцениваться одним из шести чисел: 0, 1,2, 3,4, 5, а качество продукции - одним из трех чисел: 0,1,2.

В случае непрерывной шкалы оценки могут принадлежать любой точке некоторого отрезка, который определяет шкалу данного показателя. Например, показатель выполнения плана по выпуску продукции может оцениваться десятибалльной непрерывной шкалой, т. е. оценки выбираются из отрезка [0,10] и могут быть любыми числами, принадлежащими этому отрезку. Существуют следующие способы исчисления балльной оценки для конкретного значения показателя: непрерывное отображение отрезка, в пределах которого изменяется данный показатель на заданную шкалу; с помощью задания интервалов изменения показателя и соответствующих балльных оценок.

Предположим, что известны значения показателей (матрица А), шкалы оценок по каждому показателю и способы оценки. Тогда можно построить вспомогательную матрицу В, где элементы матрицы - балльные оценки соответствующих показателей. Оценка R_i каждого подразделения i вычисляется по формуле

Критерий оценки наилучшего подразделения: max R_i (1 ≤ i ≤ п). Относительную значимость показателей в рассматриваемом методе можно задавать с помощью соответствующих нижних и верхних границ в шкалах оценок. Метод суммы баллов требует разработки большого числа шкальных оценок, которые необходимо согласовывать между собой.

Оценку методом балльной оценки необходимо провести, используя:

а) дискретную 5-балльную шкалу;

б) непрерывную шкалу на отрезке [0,5].

При этом для расчета балльных оценок по показателям-стимуляторам нужно использовать следующую формулу:

.

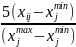Для расчета балльных оценок по показателям-дестимуляторам используйте нижеприведенную формулу:

5 - ,

где 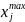и определяются как

= max x_ij (1 ≤ i ≤ m ) , = min x_ij (1 ≤ i ≤ m ), т.е. как соответственно максимальные и минимальные элементы в каждом столбце.