2. Метод абсолютных разниц

Применяется для расчета влияния факторов на прирост результативного показателя в мультипликативных и мультипликативно-аддитивных моделях типа: Y = (a-b)c и Y = a(b-c). Особенно эффективно применяется этот метод в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.

При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.

Рассмотрим алгоритм расчета для мультипликативной факторной модели типа Y=а×b.

Имеются плановые и фактические значения по каждое факторному показателю, а также их абсолютные отклонения:

а = ; b = b₁- .

Определяем изменение величины результативного показателя за счет каждого фактора по следующим формулам:

Y_a= a* ; Y_{b =} .

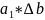Способ абсолютных разниц дает те же результаты, что и способ цепной подстановки. Здесь также необходимо следить за тем, чтобы алгебраическая сумма прироста результативного показателя за счет отдельных факторов была равна общему его приросту.

Рассмотрим алгоритм расчета факторов способом абсолютных разниц в моделях мультипликативно-аддитивного вида Y = c(a-b).

Прирост результативного показателя У за счет фактора с выражается следующей формулой:

∆У_с=∆с(a₀-b₀).

Прирост результативного показателя У за счет фактора а выражается следующей формулой:

∆У_а=с₁×∆a.

Прирост результативного показателя У за счет фактора b выражается следующей формулой:

∆У_b=с₁×(-∆b).

3. Метод относительных разниц

Применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных и аддитивно-мультипликативных моделях типа: Y=(a-b)c. Он значительно проще цепных подстановок, что при определенных обстоятельствах делает его очень эффективным. Это, прежде всего, касается тех случаев, когда исходные данные содержат уже определенные ранее относительные приросты факторных показателей в процентах или коэффициентах.

Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y=a*b*c. Сначала необходимо рассчитать относительные отклонения факторных показателей:

А%= *100%; В% = *100%; С% = 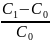*100%.

Тогда изменение результативного показателя за счет каждого фактора определяется следующим образом:

; ; .

Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитать влияние большого комплекса факторов (8-10 и более). В отличие от предыдущих способов значительно сокращается количество вычислений.

4. Индексный метод

Индексный метод основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому или по другому объекту).

С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.

Для примера возьмем индекс двухфакторной модели:

I= .

Он отражает изменение количественного показателя (а) и качественного показателя (b) и равен произведению этих индексов:

I =

Чтобы установить, как изменился индекс результативного показателя I за счет изменения факторов, необходимо рассчитать частные индексы показателей а и b:

= = .

Если из числителя вышеприведенных формул вычесть знаменатель, то получим абсолютные приросты результативного показателя в целом и за счет каждого фактора в отдельности, то есть те же результаты, что и способом цепной подстановки.