Министерство образования и науки Российской Федерации

ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Информатики и вычислительной техники

КУРСОВОЙ ПРОЕКТ

по дисциплине «Основы теории управления»

Выполнил:

студент гр. ИВТ-235

Мусагулов И. Р.

подпись, дата

Проверил:

доцент Юдин В. А.

подпись, дата

Омск 2006 г.

Задание

По заданной структурной схеме САУ (рис.1) найти:

1. Передаточную функцию разомкнутой системы W(p)

2. Передаточную функцию замкнутой системы Ф(p)

3. Передаточную функцию ошибки W_x(p)

4. Записать дифференциальное уравнение замкнутой системы

5. Записать характеристическое уравнение замкнутой системы

6. Записать дифференциальное уравнение для ошибки

7. Найти первые два коэффициента ошибки

8. Пользуясь структурным методом моделирования составить схему для моделирования САУ на ПК и рассчитать коэффициенты

9. В

   

   Рисунок 1 – Структурная схема САУ

   k₁

   

   

   

   

   

   

   

   

   

   ыбрать параметры корректирующего устройства обеспечивающий минимум интегральной оценки и построить переходный процесс при выбранных параметрах

k₁=10; k₂=2; k₃=5; k₅=1,2; T₁=0.12 c; T₂=0.15 c; ξ=0,5;

Ход работы

1. Передаточная функция разомкнутой системы W(p)

2. Передаточная функция замкнутой системы Ф(p)

3. Передаточная функция ошибки Wx(p)

4. Дифференциальное уравнение замкнутой системы

5. Характеристическое уравнение замкнутой системы

Чтобы получить характеристическое уравнение замкнутой системы необходимо сложить числитель и знаменатель передаточной функции разомкнутой системы и приравнять к нулю.

6. Дифференциальное уравнение для ошибки

7. Первые два коэффициента ошибки

Разделив числитель передаточной функции ошибки на её знаменатель, определим коэффициенты:

Для расчёта коэффициентов моделей были получены следующие коэффициенты структурной схемы:

- k₁=10;

- k₂=2;

- k₃=5;

- k₅=1,2;

- T₁=0.12 c;

- T₂=0.15 c;

- ξ=0,5;

8. Расчет коэффициентов модели и схема для моделирования САУ на ЭВМ :

1. Модель элемента сравнения сигналов.

Модель сравнения сигналов можно представить в виде суммирующего операционного усилителя. Так как не нужно усиливать сигнал, то зададим значения резисторов 1мОм.

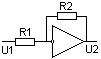
2. Масштабный операционный усилитель.

Зададим R₂=1 мОм, тогда МОм.

3. Модель идеального интегрирующего звена.

k₅=1,2 Зададим С=1 мкФ, тогда МОм.

4. Модель инерционного звена:

Для инерционного звена задаем значение С=1 мкФ, тогда R₂=T₁/C=0,15 МОм, т.к. k₃=5, то R₁=R₂/k₃ =0.03 МОм.

5. Модель колебательного звена.

k₂=2; T₁=0,12; ξ=0,5.

Зададим С=T²=0, 0144 мкФ, тогда Мом,Мом,Мом

6. Корректирующее устройство представлено реально-дифференцирующим звеном:

Задаем R₀=1 МОм, тогда R₁=T₃/k₄=0,01/0,054=0,1852МОм, R₂=T₃=0,01МОм. Коэффициенты T₃ и k₄ будут выбраны из минимума интегральной оценки.

9. Выбор параметров корректирующего устройства обеспечивающих минимум интегральной оценки

Воспользуемся интегральной оценкой вида:

dt.

Рассчитаем значения интеграла для различных и

Таблица 1 – зависимость интегральной оценки I от

k4	I
0,035	0,562
0,04	0,507
0,045	0,457
0,05	0,415
0,052	0,393
0,054	0,381
0,055	0,407

График зависимость интегральной оценки I от

Таблица 2 – зависимость интегральной оценки I от

T3	I
0,008	0,401
0,009	0,382
0,01	0,381
0,02	0,396
0,03	0,418

График зависимость интегральной оценки I от

Из таблиц 1 и 2 видно, что минимум интегральной оценки обеспечивается при следующих параметрах: k₄=0.054; T₃=0.01. Построим переходный процесс САУ с выбранными коэффициентами.

Рисунок 8 – график переходного процесса САУ

Качественные параметры переходного процесса: