Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

“ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ”

Кафедра «Информатики и Вычислительной техники»

КУРСОВОЙ ПРОЕКТ

по дисциплине «Основы теории управления»

Выполнил:

студент гр. ИВТ-254 В.В. Зобнин

подпись, дата

Проверил:

доцент В.А. Юдин

подпись, дата

Омск 2005

Содержание

Задание 4

1 Передаточная функция разомкнутой системы W(p): 5

2 Передаточная функция замкнутой системы Ф(p): 5

3 Передаточная функция ошибки системы Wx(p): 6

4 Дифференциальное уравнение замкнутой системы: 6

5 Характеристическое уравнение замкнутой системы: 6

6 Дифференциальное уравнение для ошибки: 7

7 Найдем первые два коэффициента ошибки: 7

8 Составим схему для моделирования САУ, пользуясь структурным методом: 9

8.1 Рассмотрим инерционные звенья с передаточными функциями 9

8.2 Рассмотрим колебательное звено с передаточной функцией 9

8.3 Рассмотрим идеальное интегрирующее звено с передаточной функцией 10

8.4 Рассмотрим реальное дифференцирующее звено с передаточной функцией 10

9 Выберем параметры корректирующего устройства, обеспечивающие минимум интегральной оценки: 11

Задание

Вариант №12

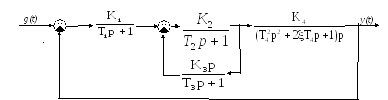
Рисунок 1 – Структурная схема системы управления

По структурной схеме, изображенной на рисунке 1, найти:

1. Передаточную функцию разомкнутой системы W(P);

2. Передаточную функцию замкнутой системы Ф(P);

3. Передаточную функцию ошибки системы W_x(P);

4. Записать дифференциальное уравнение замкнутой системы;

5. Записать характеристическое уравнение замкнутой системы;

6. Записать дифференциальное уравнение для ошибки;

7. Найти первые два коэффициента ошибки С₀,С₁;

8. Пользуясь структурными методами моделирования, составить схему для моделирования САУ на ПК и рассчитать в буквенном виде коэффициенты модели.

9. Выбрать параметры корректирующего устройства, обеспечивающие минимум интегральной оценки и для выбранных параметров построить переходный процесс в САУ.

1 Передаточная функция разомкнутой системы W(p):

(1)

тогда, подставляя значения W₁, W₂ и W₃ в (1) получаем:

; (2)

2 Передаточная функция замкнутой системы Ф(p):

;

; (3)

3 Передаточная функция ошибки системы W_x(p):

;

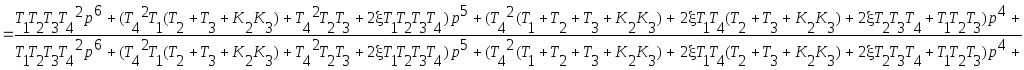
; (4)

4 Дифференциальное уравнение замкнутой системы:

;

(5)

5 Характеристическое уравнение замкнутой системы:

1+W(p)=0;

(6)

6 Дифференциальное уравнение для ошибки:

;

(7)

7 Найдем первые два коэффициента ошибки:

Чтобы получить коэффициенты ошибки, разложим передаточную функцию ошибки системы в степенной ряд:

(8)

где с₀, с₁, с₂ …— коэффициенты ошибок.

Обозначим:

L = T₁+T₂+T₃+K₂K₃+2ξT₄; M=K₁K₂K₃; N= K₁K₂K₄T₃+1;

Исходя из формулы, поделим числитель W_x(p) на ее знаменатель:

отсюда первые два коэффициента ошибки:

; (9)

; (10)

8 Составим схему для моделирования САУ, пользуясь структурным методом:

Рассчитаем коэффициенты модели и найдем их сопротивления:

К₁ = 10; T₁ = 0,12 c; К₂ = 5; T₂ = 0,15 c; K₄ = 2; T₄ = 0,08 c; ξ = 0,5.

8.1 Рассмотрим инерционные звенья с передаточными функциями

1) и 2)

Их электронная модель представлена на рисунке 3.

Рисунок 3 – Инерционное звено

Тогда 1) , и 2) , ;

, ; (11)

Рассчитаем коэффициенты для второго инерциального звена.

Примем С₁ = 1 мкФ. При Т₁ = 0,12 и K₁ = 10 имеем: R₁ = 0,012 МОм, R₂ = 0,12 МОм

Примем С₂ = 1 мкФ. При Т₂ = 0,15 и K₂ = 5 имеем: R₁ = 0,03 МОм, R₂ = 0,15 МОм.

Полученная схема САУ представлена на рисунке А.1 приложения А

8.2 Рассмотрим колебательное звено с передаточной функцией

Его электронная модель представлена на рисунке 4.

Рисунок 4 – Колебательное звено

Здесь ; ; .

Задав значение С = 1мкФ, найдем сопротивление резисторов с коэффициентами К1, К2 и К3 по формуле , где Кi – коэффициент усиления:

R(K1 = 312,5) = 0,0032 МОм;

R(K2 =156,25) = 0,0064 МОм;

R(K3 = 12,5) = 0,08 МОм;

8.3 Рассмотрим идеальное интегрирующее звено с передаточной функцией

Его электронная модель представлена на рисунке 5.

Рисунок 5 – Модель идеального интегрирующего звена

;

Задаемся значением С₁ = 1 мкФ. При k = 1 имеем: R₁ = 1МОм.

8.4 Рассмотрим реальное дифференцирующее звено с передаточной функцией

Его электронная модель представлена на рисунке 6.

Рисунок 6 – Реальное дифференцирующее звено

Тогда , и .

Рассчитаем коэффициенты:

Задаемся значением R₀ = 1 МОм. Предположим Т₃ = 0,01, тогда K2 = 100 и R₂ = 0,01 МОм. Меняя R₁ найдем значение K₃, обеспечивающее минимум интегральной оценки (см. задание 9):

; (12)

9 Выберем параметры корректирующего устройства, обеспечивающие минимум интегральной оценки:

Будем использовать интегральную оценку вида: .

Структурная схема для вычисления I имеет вид (рисунок 7):

Рисунок 7 – Схема вычисления I

На рисунке 7:

1) БВМ – блок вычисления модуля, электронная схема которого имеет вид (рисунок 8):

Рисунок 8 – Блок вычисления модуля

Пусть один из параметров реального интегрирующего звена равен: Т₃ = 0,01 при R₀ = 1 МОм.

Для нахождения минимума интегральной оценки придадим ряд фиксированных значений параметру R₁, определим К₃; определим величину I на выходе интегрирующего операционного усилителя (таблица 1).

Таблица 1 – Зависимость К₂ от I₂

К	I,	К	I,
0,005	0,27	0,03	0,17
0,01	0,175	0,04	0,2
0,015	0,165	0,045	0,23
0,02	0,162	0,05	0,27
0,025	0,16	0,055	0,34

График зависимости К от I имеет вид (рисунок 9):

Рисунок 9 – График зависимости К от I

Из рисунка 9 видно, что минимум интегральной оценки достигается при К₃ = 0,025.

Переходный процесс, для найденных параметров корректирующих устройств, представлен на рисунке 10.

Рисунок 10 – График переходного процесса

Приложение А

(обязательное)

Схема для моделирования САУ на ПК

Рисунок А.1 – Схема САУ

13