4.5. Графы и/или

Различают два основных типа стратегий управления: безвозвратный и пробный.

В безвозвратном режиме управления выбирается применимое правило и ис­пользуется необратимо, без возможности пересмотра в дальнейшем.

В пробном режиме управления выбирается применимое правило (либо произ­вольно, либо на каком-то разумном основании). Это правило используется, но резер­вируется возможность впоследствии заново вернуться к этой ситуации, чтобы при­менить другое правило.

Далее различают два типа пробных режимов управления: с возвращением и по­иском на графе.

В режиме с возвращением при выборе правила определяется некоторая точка возврата. Если последующие вычисления приведут к трудностям в построении ре­шения, то процесс вычисления переходит к предыдущей точке возврата, где приме­няется другое правило, и процесс продолжается.

Во втором типе пробного режима, который называют управление с поиском па графе, предусмотрено запоминание результатов применения одновременно не­скольких последовательностей правил. Здесь используются различные виды графо­вых структур и процедур поиска на графе.

Рассмотрим систему с исходной базой данных (С, В, Z), правила продукций ко­торой основаны на следующих правилах переписывания.

П1: С  (D, L); П2: С  (В, М); ПЗ: В  (М, М); П4: Z  (В, В, М),

а терминальное условие состоит в том, что эта база данных должна содержать только символ М.

Исходная база данных разлагается на составляющие С, В и Z. Правила продук­ций применимы независимо к каждой составляющей (возможно, параллельно). Ре­зультаты этих операций также подвергаются декомпозиции и так далее, пока каждая компонента базы данных не будет содержать только символы М.

Как и в случае обычных графов, граф типа И/ИЛИ состоит из вершин, поме­ченных глобальными базами данных. Вершины, помеченные составными базами данных, имеют множество вершин преемников, каждая из которых помечена одной из составляющих. Эти вершимы преемники называются вершинами типа И, так как для полной обработки составной базы данных должны быть обработаны полностью все ее составляющие.

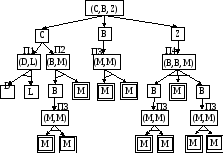
Рис. 6

Множество вершин типа И (рис. 6) обозначаются дугой, объединяющей входящие в них дуги графа, которая называется k-связкой (k  число вершин преемников).

К составляющим базам данных можно применять правила. Вершины, помечен­ные этими составляющими базами данных, имеют вершины-преемники, которые помечены базами, полученными в результате применения правил. Эти вершины-преемники называют вершинами типа ИЛИ, поскольку для полной обработки со­ставляющей базы данных полностью должна быть обработана база данных, порож­денная в результате применения лишь одного из правил.

На рисунке 6 все вершины, соответствующие какой-либо составляющей базе данных, удовлетворяющей терминальному условию, заключены в двойную рамку. Такие вершины называются терминальными.

Глава 5. Нечеткие знания

При попытке формализовать человеческие знания исследователи вскоре столк­ну­лись с проблемой, затруднявшей использование традиционного математиче­ского ап­парата для их описания. Существует целый класс описаний, оперирую­щих качествен­ными характеристиками объектов (много, мало, сильный, очень сильный и т. п.). Эти характеристики обычно размыты и не могут быть однознач­но интерпретированы, од­нако содержат важную информацию (например, «Од­ним из возможных признаков гриппа является высокая температура»).

Кроме того, в задачах, решаемых интеллектуальными системами, часто прихо­дится пользоваться неточными знаниями, которые не могут быть интерпретиро­ваны как полностью истинные или ложные (логические true/false или 0/1). Су­ществуют знания, достоверность которых выражается некоторой промежуточной цифрой, напри­мер 0,7.

Как, не разрушая свойства размытости и неточности, представлять подобные зна­ния формально? Для разрешения таких проблем в начале 70-х американский ма­тематик Лотфи Заде предложил формальный аппарат нечеткой (fuzzy) алгебры и нечеткой ло­гики. Позднее это направление получило широкое рас­пространение и положило на­чало одной из ветвей ИИ под названием  мягкие вычисления (soft computing).

Л. Заде ввел одно из главных понятий в нечеткой логике  понятие лингвисти­че­ской переменной.

Лингвистическая переменная (ЛП)  это переменная, значение которой опре­деляется набором вербальных (то есть словесных) характеристик некоторого свой­ства.

Например, ЛП «рост» определяется через набор {карликовый, низкий, средний, высокий, очень высокий}.