4 Релятивістський закон додавання швидкостей

Розглянемо рух матеріальної точки в системі , яка рухається відносно системи K із швидкістю u. Якщо в системі K рух точки в кожний момент часу t визначається координатами x, y, z, а в системі в момент часу t – координатами 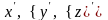, то

, , ,

, ,

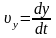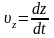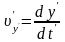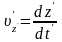
є проекціями вектора швидкості точки відносно систем K і на відповідні координатні осі. Використаємо перетворення Лоренца

, , ,

, .

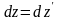Розділимо перші три рівності на четверту:

,

,

.

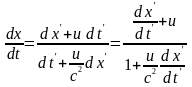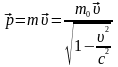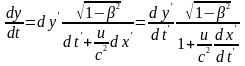В результаті отримуємо формули перетворення швидкостей при переході від однієї системи відліку до іншої:

, ,

.

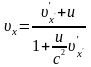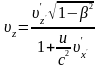Аналогічно

, ,

.

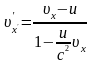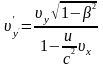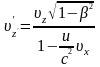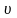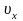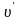Якщо матеріальна точка рухається паралельно до осі X, то швидкість відносно системи K збігається з , а швидкість відносно – з 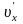. Тоді

, .

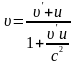Якщо швидкості 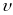, 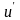і u малі порівняно з швидкістю c, то , .

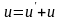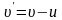Якщ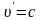о , то

.

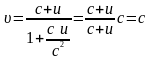Нехай .

.

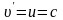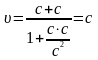При додаванні довільних швидкостей їх сума не може перевищити швидкості світла c у вакуумі.

5 Елементи релятивістської динаміки. Взаємозв’язок маси і енергії

Другий закон Ньютона для матеріальної точки

або ,

в якому маса m точки вважається сталою і однаковою у всіх інерціальних системах відліку, виявляється не інваріантним по відношенню до перетворення Лоренца. Отже, цей закон не може служити основою релятивістської динаміки.

У релятивістській механіці, як і в ньютонівській, імпульс 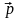матеріальної точки пропорційний до її маси m і збігається за напрямком з швидкістю цієї точки. Проте, на відміну від ньютонівської механіки, імпульс матеріальної точки є нелінійною функцією її швидкості:

,

де 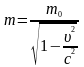– релятивістська маса, а 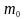– маса спокою матеріальної точки, тобто маса, яка виміряна в тій інерціальній системі відліку, відносно якої матеріальна точка знаходиться в стані спокою.

Основний закон релятивістської динаміки: швидкість зміни імпульсу матеріальної точки дорівнює силі , що діє на цю точку, тобто ,

.

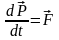Елементарна робота сили на малому переміщенні 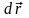точки її прикладення дорівнює:

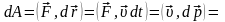
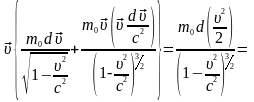
(тут враховано, що )

.

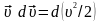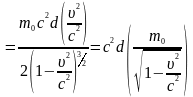Приріст кінетичної енергії 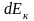матеріальної точки дорівнює роботі :

.

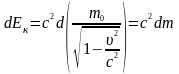Інтегруючи отримане співвідношення, маємо:

.

При 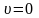, 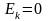і .

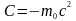Отже, релятивістський вираз для кінетичної енергії частинки має вигляд:

.

При 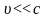, 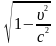розкладемо в ряд, обмежившись членами другого порядку малості:

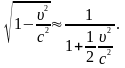
Тоді

.

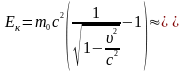
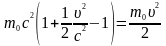Ейнштейн узагальнив положення 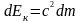, передбачивши, що воно справедливе не лише для кінетичної енергії матеріальної точки, але і для повної енергії, а саме: довільна зміна маси Δ m супроводжується зміною повної енергії матеріальної точки:

.

.

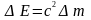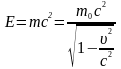Це рівняння виражає закон взаємозв’язку маси і енергії.

Знайдемо релятивістську залежність між повною енергією й імпульсом частинки:

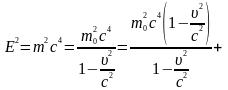
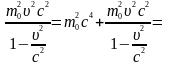
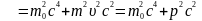
і

.

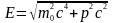Якщо тіло нерухоме, то 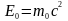, де 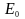– енергія спокою тіла.

Приклади розв’язування задач

Задача 1 Довжина лінійки, яка нерухома відносно земного спостерігача, 2 м. Яка довжина цієї лінійки, якщо вона рухається зі швидкістю 0,5 швидкості світла?

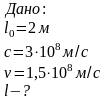
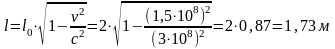
Відповідь: 1.73 м.

Задача 2 У скільки разів сповільнюється інтервал часу (по годиннику «нерухомого» спостерігача) при швидкості 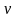=27000км/с?

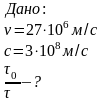
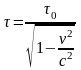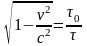; 4

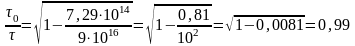
Відповідь: 0,99.

Задача 3 З якою швидкістю повинен рухатися космічний корабель, щоб його шлях при вимірюванні з Землі був у 2 рази менший?

; ;

; ;

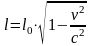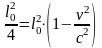
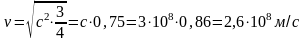
Відповідь: 2,6·10⁸ м/с.

Задача 4 Електрон і протон рухаються назустріч один одному відносно нерухомого спостерігача з швидкостями 2·10⁸ і 2,5·10⁸ м/с. Знайти швидкість цих частинок одна відносно одної, виходячи з релятивістської і класичної формул додавання швидкостей. Результати порівняти.

Д ано: Розв’язання

υ₁= 2·10⁸ м/с За релятивістською формулою додавання швидкостей

υ₂= 2,5·10⁸ м/с

υ_p - ? υ_k - ? 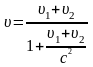= 2,6·10⁸ м/с

За класичною формулою Галілея υ_k=υ₁+ υ₂ = 4,5·10⁸ м/с, тобто υ_k > c, що неможливо.

Відповідь: 2,6·10⁸ м/с; 4,5·10⁸ м/с.

Задача 5 Синхрофазоторон дає пучок протонів, швидкість яких дорівнює 0,99с(де с-швидкість світла у вакуумі). Знайти: 1) масу протонів; 2) зменшення розмірів протонів у напрямі їх руху; 3) час, з точки зору земного спостерігача, який відповідає проміжку часу в 1с, виміряному годинником, зв’язаним з протоном; 4) кінетичну енергію протона. Масу спокою протона вважати такою, що дорівнює 1,67·10^-27 кг.

Д ано: Розв’язання

m₀=1,67·10^-27 кг Знаходимо масу за формулою

τ=1 с

υ =0,99 с = 1,19·10^-26 кг ; 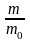= 7,15, тобто маса протона зростає у 7,15 раз

m-? -? τ₀-? E_к-? Знаходимо зміну розмірів протона з формули = ; =0,14; =0,14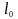

Обчислюємо інтервал часу для нерухомого відносно Землі спостерігача

τ₀=τ ; τ₀=0,14 с

Знаходимо кінетичну енергію протона як різницю повної енергії E₁, що відповідає швидкості руху υ і енергії E₀ спокою протона

E_к= E₁-E_0, E₁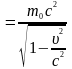 , ; E_к=9,24·10^-10 Дж = 5780 МеВ

Відповідь: 1,19·10^-26 кг, =0,14 , 0,14 с, 5780 МеВ.

Задача 6 Сонце щосекунди випромінює енергію, що дорівнює 1,08·10²⁰ кВт·год. Знайти зміну маси Сонця за цей час. Через скільки часу маса Сонця становитиме 0,9 маси на даний момент часу? Вважати випромінювання Сонця рівномірним, а його масу такою, що дорівнює 1,97·10³⁰ кг.

Дано: Розв’язання

Δ E=1,08·10²⁰кВт·год= Зміну маси Сонця за 1 с знаходимо з формули , де

=3,93·10²⁶ Дж Δm =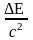 = 4,37·10⁹ кг

m₀= 1,97·10³⁰ кг Обчислимо інтервал часу, протягом якого маса Сонця стане рівною

t=1 с 0,9 m₀, тобто Сонце втратить десяту частину своєї маси:

m=0,9 m₀ Δt=(0,1·1,97·10³⁰):4,37·10⁹=4,5·10¹⁹ (с)=1,42·10¹² років

c=3·10⁸ м/с

Δm-? Δt-?

Відповідь: 4,37·10⁹ кг, 1,42·10¹² років.

ЗАВДАННЯ: законспектувати запитання плану.

ФОРМА КОНТРОЛЮ: виконання тестів.