
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Тульский государственный университет»
Кафедра
«Автоматизированные информационные и управляющие системы»
Методические указания
к выполнению
контрольно-курсовой работе
по дисциплине
Практикум по теории статистики и многомерному статанализу
Направление подготовки (cпециальность): 230100 Информатика и вычислительная техника
Профиль «Автоматизированные системы обработки информации и управления»
Квалификация (степень) выпускника: 62 бакалавр
Тула 2012
Методические указания составлены доц., к.т.н. Арефьевой Е.А. и обсуждены на заседании кафедры АИУС факультета ЭиМ
Протокол № от .
Зав. кафедрой В.А.Фатуев
Методические указания пересмотрены и утверждены на заседании кафедры АИУС факультета ЭиМ
Протокол № от .
Зав. кафедрой В.А.Фатуев
Цель и задачи исследования
Изучение и приобретение навыков построения регрессионных моделей.
Общее
назначение регрессионного анализа
состоит в аналитическом выражении связи
между одной или несколькими независимыми
переменными
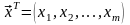 (называемыми также регрессорами,
факторными или экзогенными признаками)
и зависимой переменной
(называемыми также регрессорами,
факторными или экзогенными признаками)
и зависимой переменной
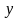 (результирующим или эндогенным признаком):
(результирующим или эндогенным признаком):
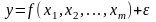 . (5.25)
. (5.25)
Регрессия – это условное математическое ожидание (зависимость математического ожидания выходной переменной от ожидания входной):
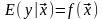 .
.
При регрессионном анализе решаются следующие задачи:
Установление форм зависимости между переменными (идентификация);
Определение функции регрессии (сводится к определению неизвестных параметров модели);
Оценка неизвестных значений зависимой переменной (прогнозирование).
В зависимости от количества регрессоров различают парную (один регрессор) и множественную регрессию. Так, уравнение парной регрессии определяет зависимость результирующей переменной от одной независимой, а множественной регрессии – от нескольких независимых переменных. В зависимости от вида связи между факторами различают линейную и нелинейную регрессию.
Линейная регрессионная модель имеет вид
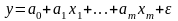 .
(5.26)
.
(5.26)
Линейные модели (в более общем случае - линейно-параметризованные) могут быть записаны в виде скалярного произведения вектора неизвестных коэффициентов и вектора базисных функций:
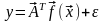 ,
(5.27)
,
(5.27)
где
 ,
,
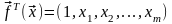 ,
,
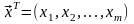 .
.
Нелинейно-параметризованную модель нельзя представить в виде подобного скалярного произведения, т.е.
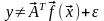 . (5.28)
. (5.28)
Общая вычислительная задача, которую требуется решать при анализе методом регрессии, состоит в подгонке некоторой функции к заданному набору точек. Линия регрессии выражает наилучшее предсказание зависимой переменной по независимым переменным. Однако природа редко (если вообще когда-нибудь) бывает полностью предсказуемой и обычно имеется существенный разброс наблюдаемых точек относительно подогнанной прямой (как показано на диаграмме рассеяния). Очевидно, что, чем меньше разброс значений остатков около линии регрессии по отношению к общему разбросу значений, тем лучше построена модель регрессии.
Из всего множества всевозможных математических функций для построения регрессионных зависимостей в социально-экономической сфере обычно используют сравнительно небольшое их число. Это объясняется реально существующими типами изменений, с которыми приходится сталкиваться исследователю. Рассмотрим наиболее часто используемые математические зависимости (для случая парной регрессии).
Полиномиальные функции. Эти модели имеют вид
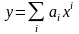 . (5.29)
. (5.29)
В
зависимости от диапазона изменения
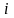 получаем различные модели.
получаем различные модели.
При
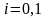 имеем линейную функцию. Она описывается
уравнением вида
имеем линейную функцию. Она описывается
уравнением вида
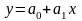 ,
(5.30)
,
(5.30)
где
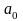 -
показатель в начальный момент,
-
показатель в начальный момент,
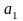 -
прирост за единицу времени.
-
прирост за единицу времени.
Для этого типа характерно изменение исследуемого показателя за каждый период на одну и ту же величину. Линейная функция является полиномиальной функцией первого порядка. Пример линейной функции приведен на рис. 5.5.
Если
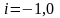 ,
то функция – гиперболическая
,
то функция – гиперболическая
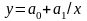 (рис. 5.6).
(рис. 5.6).


Рис. 5.5. Линейная функция Рис. 5.6. Гиперболическая функция
При
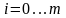 имеем полином степени
имеем полином степени
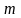 .
Полином 5-й степени приведен на рис. 5.7.
.
Полином 5-й степени приведен на рис. 5.7.
Э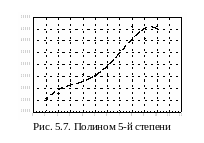 кспоненциальные
функции. В общем случае этот вид
моделей может быть представлен следующим
образом:
кспоненциальные
функции. В общем случае этот вид
моделей может быть представлен следующим
образом:
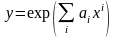 . (5.31)
. (5.31)
При
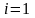 приходим к общеизвестной модели
экспоненциального роста первого порядка:
приходим к общеизвестной модели
экспоненциального роста первого порядка:
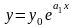 ,
(5.32)
,
(5.32)
где
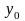 —
начальный уровень,
—
начальный уровень,
- средний темп роста.
График этой функции имеет вид, показанный на рис. 5.8.
Экспоненциальный рост предполагает относительно постоянное и быстрое возрастание уровня изучаемого явления, т.е. изменение с постоянным темпом прироста или по сложным процентам, по геометрической прогрессии.
Необычайно широкое применение модели экспоненциального роста объясняется чаще всего природой процесса воспроизводства. Под воспроизводством понимается процесс, при котором биологические и социальные системы (или элементы систем) воспроизводят подобных себе. Очевидно, что объем воспроизводства зависит от исходного уровня: чем больше начальное число элементов, способных к воспроизводству, тем больше будет прирост новых элементов.
У экспоненциальной модели есть свои недостатки. В большинстве случаев для реального процесса характерны изменяющиеся темпы роста, поэтому экспоненциальный рост должен рано или поздно столкнуться с ограничениями внешней среды.
S-образные функции. К этому классу относят логистическую функцию и кривую Гомперца.
Как видно из графика (рис. 5.9), логистическая функция предполагает, что сначала происходит рост с увеличивающимися абсолютными приростами, затем после точки перегиба он замедляется, и процесс постепенно приближается к пределу, т.е. к некоторой постоянной величине. Математическая модель логистического роста имеет следующий вид:
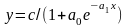 ,
(5.33)
,
(5.33)
где
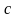 - предел роста;
- предел роста;
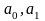 -
параметры процесса, причем первый
параметр характеризует положение кривой
на оси времени, а второй – крутизну
кривой.
-
параметры процесса, причем первый
параметр характеризует положение кривой
на оси времени, а второй – крутизну
кривой.
Кривая Гомперца сходна с логистой и описывается уравнением
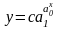 . (5.34)
. (5.34)
Параметры функции имеют тот же смысл, что и у логистической кривой.


Рис. 5.8. Экспоненциальная функция Рис. 5.9. Логистическая функция
Задача
оценки параметров регрессионной модели
заключается в оценке вектора неизвестных
параметров
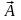 на основе наблюдений и измерений
процессов
на основе наблюдений и измерений
процессов
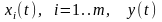 .
Оценка этого вектора представляет собой
векторную случайную величину, т.е.
совокупность случайных величин.
.
Оценка этого вектора представляет собой
векторную случайную величину, т.е.
совокупность случайных величин.
Для оценивания неизвестных параметров линейно-параметризованной модели может быть использован метод наименьших квадратов (МНК), метод максимального правдоподобия, а в случае нелинейной параметризации – методы нелинейного оценивания.
Метод наименьших квадратов. Рассмотрим случай линейной регрессии. Требуется построить прямую линию, которая наиболее точно отображала бы изменения динамики за рассматриваемый период. Поскольку исходные значения имеют колебания, то модель будет содержать ошибки, которые и надо минимизировать. Наиболее объективным с формальной точки зрения будет построение, основанное на минимизации суммы отрицательных и положительных отклонений исходных значений от прямой линии, и, как следствие, наиболее используемой процедурой является минимизация суммы квадратов отклонений или метод наименьших квадратов.
Использование метода предполагает соблюдение некоторых условий: остатки имеют математическое ожидание, равное нулю, и конечную дисперсию, подчинена нормальному закону распределения; отсутствует мультиколлинеарность.
Найдем
оценку вектора
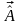 ,
решив следующую экстремальную задачу:
,
решив следующую экстремальную задачу:
 . (5.35)
. (5.35)
Требуется найти такой вектор , при котором сумма квадратов остатков была бы минимальна:
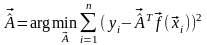 . (5.36)
. (5.36)
Найдем решение этой задачи для парной линейной регрессии:
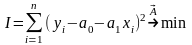 . (5.37)
. (5.37)
Проводя дифференцирование функции по неизвестным параметрам, получаем
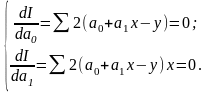 (5.38)
(5.38)
Отсюда имеем систему нормальных уравнений
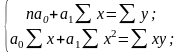 (5.39)
(5.39)
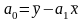 ,
(5.40)
,
(5.40)
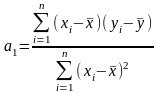 . (5.41)
. (5.41)
В более общем случае решением поставленной задачи является вектор, определяемый по формуле
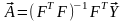 , (5.42)
, (5.42)
где
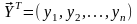 - вектор значений
зависимой переменной в
- вектор значений
зависимой переменной в
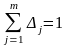 измерениях;
измерениях;
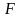 -
матрица базисных функций размерностью
-
матрица базисных функций размерностью
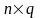 :
:
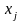
Так, для однофакторной линейной модели получаем
 ,
,
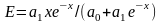 ,
,
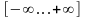 .
.
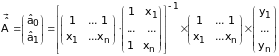 .
.
Одна из главных предпосылок использования МНК - отсутствие линейной зависимости между независимыми переменными. Мультиколлинеарность возникает тогда, когда существует высокая корреляция (но не функциональная связь) между двумя и более переменными. Опасность этого кроется в росте дисперсии коэффициента регрессии, а значит, и в росте ошибки их оценивания. Проблема мультиколлинеарности является общей для многих методов корреляционного анализа. Если в анализ включено много переменных, то часто не сразу очевидно существование этой проблемы, и она может возникнуть только после того, как некоторые переменные будут уже включены в регрессионное уравнение. Тем не менее, если такая проблема возникает, это означает, что, по крайней мере, одна из независимых переменных является лишней при наличии остальных. Существует довольно много статистических индикаторов избыточности (толерантность, частные корреляции и др.), а также немало средств для борьбы с избыточностью.
Метод максимального правдоподобия. По принципу максимального правдоподобия за оценку неизвестных параметров принимают такое значение, которое представляется наиболее вероятным на основании опытных данных.
Пусть
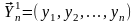 - случайные величины, имеющие какое-то
распределение,
- случайные величины, имеющие какое-то
распределение,
 -
плотность распределения.
-
плотность распределения.
Поскольку
источником распределения случайных
величин
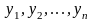 является наличие случайной величины
является наличие случайной величины
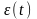 ,
то законы распределения
совпадают с законом распределения
.
Параметры распределения разные, причем
математическое ожидание разное, а
дисперсии при стационарном случайном
процессе
одинаковы.
,
то законы распределения
совпадают с законом распределения
.
Параметры распределения разные, причем
математическое ожидание разное, а
дисперсии при стационарном случайном
процессе
одинаковы.
Зная плотности распределения, можно вычислить функцию правдоподобия:
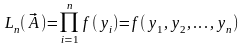 . (5.43)
. (5.43)
В
частном случае, если измерения независимы,
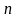 -мерная
плотность распределения равна
произведению
-мерная
плотность распределения равна
произведению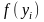 .
.
Функция правдоподобия зависит от неизвестных параметров.
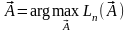 -
это оценка максимального правдоподобия.
-
это оценка максимального правдоподобия.
Оценка максимального правдоподобия максимизирует функцию правдоподобия. Согласно принципу максимального правдоподобия за оценку параметров принимают значения, при которых функция правдоподобия достигает максимума.
Для упрощения вычислений обычно максимизируют не исходную функцию правдоподобия, а логарифмическую функцию правдоподобия:
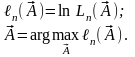 (5.44)
(5.44)
Прежде чем использовать регрессионную модель, целесообразно провести проверку значимости модели и проверку адекватности представления исходных данных полученному уравнению регрессии, в результате чего происходит уточнение структуры модели с обоснованием правильности ее выбора.
Проверка значимости модели состоит из двух этапов: проверка значимости модели в целом и проверки значимости ее параметров.
Значимость
модели определяется путем проверки
существенности отличия от нуля
коэффициента множественной корреляции
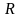 :
:
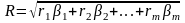 , (5.45)
, (5.45)
где
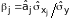 - коэффициент регрессии в стандартизованном
виде, используемый для устранения
различий в измерении и степени колеблемости
факторов;
- коэффициент регрессии в стандартизованном
виде, используемый для устранения
различий в измерении и степени колеблемости
факторов;
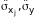 -
оценки СКО
-
оценки СКО
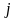 -й
и независимой переменных соответственно;
-й
и независимой переменных соответственно;
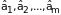 -
оценки соответствующих регрессионных
коэффициентов;
-
оценки соответствующих регрессионных
коэффициентов;
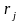 -
коэффициент парной корреляции между
-ой
и зависимой переменными.
-
коэффициент парной корреляции между
-ой
и зависимой переменными.
Коэффициент парной корреляции используется для определения степени тесноты связи объясняемой и независимой переменными после вычленения влияния всех остальных переменных. Коэффициент показывает, на какую часть величины СКО меняется среднее значение зависимой переменной с изменением соответствующей независимой переменной на одно среднеквадратическое отклонение при фиксированном постоянном уровне значений остальных независимых переменных.
Коэффициент
множественной детерминации
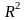 показывает удельный вес совместного
влияния всех включенных в модель
регрессоров на зависимую переменную.
Параметр
показывает удельный вес совместного
влияния всех включенных в модель
регрессоров на зависимую переменную.
Параметр
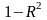 определяет степень влияния на
результативный признак всех неучтенных
в модели факторов.
определяет степень влияния на
результативный признак всех неучтенных
в модели факторов.
Кроме
проверки значимости всей модели
необходимо проверить (оценить)
регрессионные коэффициенты на их отличие
от нуля. Проверка значимости
-го
коэффициента модели эквивалентна
проверке гипотезы о том, что
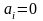 (нуль-гипотеза). Проверка гипотезы
осуществляется с использованием критерия
Стьюдента:
(нуль-гипотеза). Проверка гипотезы
осуществляется с использованием критерия
Стьюдента:
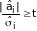 , (5.46)
, (5.46)
где
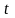 - это квантиль распределения Стьюдента,
соответствующий уровню значимости
- это квантиль распределения Стьюдента,
соответствующий уровню значимости
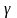 и числу степеней свободы
и числу степеней свободы
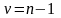 ;
;
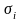 -
среднеквадратическое отклонение
-го
параметра модели:
-
среднеквадратическое отклонение
-го
параметра модели:
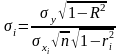 .
.
После проверки значимости все незначащие коэффициенты исключаются из модели, т.е. осуществляется корректировка ее структуры.
Проверка точности представления исходных данных полученному уравнению регрессии осуществляется на основе анализа остатков. Анализ отклонений от линии регрессии (остатков) позволяет определить, насколько оцененная регрессия отражает реальные данные. Хорошая регрессия та, которая объясняет значительную долю дисперсии, и, наоборот, плохая регрессия не отслеживает большую часть колебаний исходных данных.
Для
оценки уравнения регрессии используются
общая дисперсия результативного признака
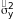 ;
факторная дисперсия результативного
признака, отображающая вариацию
;
факторная дисперсия результативного
признака, отображающая вариацию
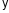 от воздействия входных факторов модели
от воздействия входных факторов модели
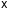 ;
дисперсия остатков модели (дисперсия
адекватности), отражающая вариацию
результативного признака относительно
модели.
;
дисперсия остатков модели (дисперсия
адекватности), отражающая вариацию
результативного признака относительно
модели.
Факторная дисперсия результативного признака и дисперсия остатков модели определяются по формулам (5.47) и (5.48) соответственно.
 , (5.47)
, (5.47)
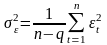 , (5.48)
, (5.48)
где
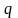 -
число параметров модели.
-
число параметров модели.
Индекс детерминации определяет долю факторной дисперсии в общей и характеризует, какая часть общей вариации результативного признака характеризуется входными факторами:
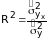 ,
,
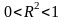 . (5.49)
. (5.49)
Для оценки значимости индекса детерминации применяется F-критерий Фишера, значение которого определяется по формуле:
 . (5.50)
. (5.50)
Полученная
величина сравнивается с критическим
значением, которое определяется по
таблице F-распределения
с учетом принятого уровня значимости
и числа степеней свободы (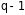 и
и
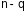 )
и делается вывод о значимости уравнения
регрессии.
)
и делается вывод о значимости уравнения
регрессии.
Для оценки точности уравнения регрессии может быть использована относительная ошибка аппроксимации:
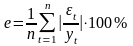 .
(5.51)
.
(5.51)
Модель
считается достаточно точной, если
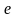 меньше 10…20 %.
меньше 10…20 %.
На основе регрессионного анализа можно определить отдельное влияние факторных признаков на результативный признак, для чего могут быть использованы дельта-коэффициенты и коэффициенты эластичности.
Дельта-коэффициент. Дельта-коэффициент определяет долю вклада каждого фактора в суммарное влияние на выход:
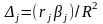 ,
. (5.52)
,
. (5.52)
При корректно проводимом регрессионном анализе все величины дельта-коэффициентов положительны, т.е. все коэффициенты регрессии имеют тот же знак, что и соответствующие коэффициенты парной корреляции. Только в случае мультиколлинеарности дельта-коэффициенты могут быть отрицательны.
Коэффициент эластичности. Влияние факторных признаков на результативный часто определяют также с использованием коэффициента эластичности. Эластичность по отношению к рассчитывается как процентное изменение , отнесенное к соответствующему процентному изменению . В общем случае эластичности не постоянны, они различаются, если измерены для различных точек на линии регрессии. По умолчанию стандартные программы, оценивающие эластичность, вычисляют ее в точках средних значений:
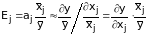 . (5.53)
. (5.53)
Формулы расчета коэффициента эластичности для некоторых распространенных моделей приведены в табл. 5.6.
Таблица 5.6
Коэффициенты эластичности для отдельных уравнений регрессии
-
Регрессионное уравнение
Коэффициент эластичности
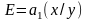
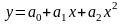
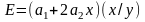
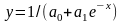
Эластичность
ненормирована и может изменяться в
диапазоне
.
Важно, что она безразмерна, так что
интерпретация эластичности
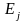 =2.0
означает, что если
=2.0
означает, что если
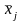 увеличится (уменьшится) на 1 %, то это
приведет к увеличению (уменьшению)
увеличится (уменьшится) на 1 %, то это
приведет к увеличению (уменьшению)
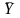 на
2 %. Если
=
-0.5, то это означает, что увеличение
на 1 % приведет к уменьшению
на
0.5 %.
на
2 %. Если
=
-0.5, то это означает, что увеличение
на 1 % приведет к уменьшению
на
0.5 %.
Высокий уровень эластичности означает сильное влияние независимой переменной на объясняемую переменную.
