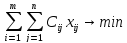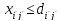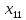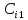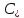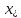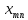Теоретическая часть.

Построение математической модели.

Пусть - количество едениц продукта, поставляемого из пункта в пункт . Подлежащие минимизации суммарные затраты на перевозку продуктов из всех пунктов производства во все пункты потребления выражаются формулой:

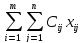
Суммарное количество продукта, направляемого из каждого пункта отправления во все пункты назначения, должно быть равно запасу продукта в данном пункте. То есть:

Суммарное количество груза, доставляемого в каждый пункт назначения из всех пунктов отправления, должно быть равно потребности. Это условие полного удовлетворения спроса:

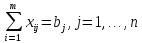
Пункты отправления	Пункты назначения						Запасы
		…		…
		…		…
…	…	…	…	…	…	…
		…		…
…	…	…	…	…	…	…
		…		…
Потребности		…		…

Также необходимо отметить, что объемы перевозок - неотрицательные числа, так как перевозки из пунктов потребления в пункты производства исключены:

Помимо неотрицательности перевозок, в задаче существует ограничение на пропускную способность для какого либо 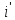и т.е.

Исходя выше приведённых данных, транспортная задача сводится к минимизации суммарных затрат при выполнении условий полного удовлетворения спроса и равенства вывозимого количества продукта запасам его в пунктах отправления.

Для удобства необходимо определить понятие опорного плана транспортной задачи:

определяемое матрицей =()(; ), называется планом транспортной задачи.

План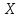=()(; ), при котором функция

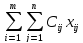
принимает свое минимальное значение, называется оптимальным планом транспортной задачи.

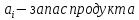
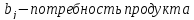
– конкретный потребитель

– конкретный поставщик

7