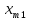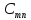Постановка задачи.

Транспортная задача является частным типом задачи линейного программирования. Её формулировка такова:

Имеется пунктов отправления (или пунктов производства) , в которых сосредоточены запасы однородных продуктов в количестве единиц.

Имеется пунктов назначения (или пунктов потребления) потребность которых в указанных продуктах составляет единиц.

Известны также транспортные расходы , связанные с перевозкой единицы продукта из пункта в пункт , где

Допустим, что

т. е. общий объем производства равен общему объему потребления.

Требуется составить такой оптимальный план перевозок, чтобы удовлетворить спрос всех пунктов потребления за счет продукта, произведенного всеми пунктами производства, при минимальной общей стоимости всех перевозок.

Приведенная формулировка транспортной задачи называется закрытой моделью. В том случае, если общий объём производства не равен общему объёму потребления, то такая модель называется открытой. Открытая модель решается приведением её к закрытой модели.

Математическая формулировка.

Пусть - количество едениц продукта, поставляемого из пункта в пункт . Подлежащие минимизации суммарные затраты на перевозку продуктов из всех пунктов производства во все пункты потребления выражаются формулой:

Суммарное количество продукта, направляемого из каждого пункта отправления во все пункты назначения, должно быть равно запасу продукта в данном пункте. То есть:

Суммарное количество груза, доставляемого в каждый пункт назначения из всех пунктов отправления, должно быть равно потребности. Это условие полного удовлетворения спроса:

Пункты отправления	Пункты назначения						Запасы
		…		…
		…		…
…	…	…	…	…	…	…
		…		…
…	…	…	…	…	…	…
		…		…
Потребности		…		…

Также необходимо отметить, что объемы перевозок - неотрицательные числа, так как перевозки из пунктов потребления в пункты производства исключены:

Исходя выше приведённых данных, транспортная задача сводится к минимизации суммарных затрат при выполнении условий полного удовлетворения спроса и равенства вывозимого количества продукта запасам его в пунктах отправления.

Для удобства необходимо определить понятие опорного плана транспортной задачи:

всякое неотрицательное решение системы линейных уравнений

определяемое матрицей =()(; ), называется планом транспортной задачи.

План=()(; ), при котором функция

принимает свое минимальное значение, называется оптимальным планом транспортной задачи.

В итоге математическая модель классической транспортной задачи линейного программирования, будет выглядеть так: