16. Идеальные растворы. Законы Рауля.

Раствор это гомогенная система, состоящая из некоторых компонентов

Растворы образуется самопроизвольно, при образовании растворов происходит взаимодействие между растворенным веществом или растворителем.

Идеальный раствор – раствор, в котором силы взаимодействия между разноимёнными молекулами такие же как и между одноимёнными:

F1,1=F1,2=F2,2 , H=0 и V=0.

Оба компонента подчиняются закону Рауля.

В 1887 году французский ученый Рауль установил следующий закон: для разбавленных растворов неэлектролитов при постоянной температуре понижение давления пара пропорционально мольнойдоле растворенного вещества:

или при n << N, ,

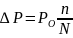где n – число молей растворенного вещества; N – число молей растворителя; РО – давление пара чистого растворителя; Р – давление пара растворителя над этим раствором.

17. Температура замерзания и кипения растворов. Криоскопия и эбуллиоскопия. Определение молекулярной массы растворенного вещества.

Так как при растворении в растворителе нелетучего вещества давление пара растворителя над раствором уменьшается, это вызывает повышение температуры кипения раствора и понижение температуры его замерзания (по сравнению с чистым растворителем).

Чистая вода при нормальном атмосферном давлении кипит при 100°С (373,15К), так как при этой температуре давление водяного пара равно внешнему давлению. Для того чтобы закипел раствор, давление пара растворителя также должно быть равно атмосферному. Однако это имеет место при более высокой температуре t''к, чем для чистого растворителя t' к.

Жидкость затвердевает, когда давление ее пара становится равным давлению пара соответствующей твердой фазы. что давление пара льда достигается у раствора при более низкой температуре t'₃, чем давление чистой воды t''₃. Понижение температуры

замерзания растворов было впервые установлено М. В. Ломоносовым (1748 г.).

Исследование свойств разбавленных растворов неэлектролитов показало, что понижение давления пара, повышение температуры кипения и понижение температуры замерзания обусловлены только числом растворенных частиц в определенном количестве данного растворителя и не зависят от природы растворенного вещества. В этом заключается сущность законов Рауля.

В общем виде зависимость понижения температуры замерзания ΔТ₃, повышения температуры кипения ΔТ_к разбавленных растворов от концентрации неэлектролита (второй закон Рауля) можно записать так:

ΔТ₃ = К₃ · C и Δt_k = Е_k · C,

где К₃, Е_k – коэффициенты пропорциональности, зависящие от природы растворителя; С – концентрация растворенного вещества (число молей в 100 г растворителе).

Коэффициенты пропорциональности К3 и Еk называют соответственно криоскопической и эбуллиоскопической кoнстантами.

Свойства, количественное выражение которых зависит только от числа находящихся в растворе частиц растворенного вещества и количества растворителя, называют коллигативными свойствами. Некоторые коллигативные свойства растворов используются для определения молекулярной массы растворенного вещества. Для этого в уравнении для Δt концентрацию заменяют отношением массы растворенного вещества в 1000 г растворителя m к молярной массе этого вещества М, тогда Δt = R · (m/М).

С помощью этой формулы, зная экспериментальные значения Δt, нетрудно подсчитать молярную массу вещества.