Экспертные методы оценки в управление качеством продукции

Цель работы: Изучить методы организации экспертных групп по оценки качества и рассмотреть способы оценки экспертной информации, с расчетом коэффициента конкордации и критерия Пирсона.

Метод экспертных оценок это метод прогнозирования основанный на достижении согласия группой экспертов.

В задачу экспертов при проведение экспертной оценки входит расположение показателей , L –общее число показателей, в порядке их важности, придав им соответствующие ранги от 1 до L, т.е. проведение ранжирования показателей.

Если эксперт не в состоянии четко указать порядок убывания важности 2 или 3 показателей, он присваивает им одинаковый ранг равный среднему арифметическому номеров их мест.

Для оценки согласованности мнения экспертов определяется коэффициент конкордации по формуле Кендалла

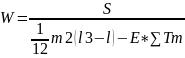,где m – число экспертов, L – число показателей, S – сумма квадратов отклонений, суммы рангов каждого показателя от средней суммы рангов, e – число экспертов не сумевших различить показатели, Tm – поправочный коэффициент для m эксперта.

S = ∑ [∑r - 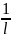∑(∑r)]² ,где r – ранг I показателя у j эксперта.

Tm = 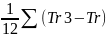Tr - число показателей с одинаковым индексом r, по данным m эксперта.

T = - поправочный коэффициент.

Если все эксперты сумели различить все ранги, то E = 0, а

W =

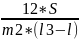
Пример:

6 Экспертов ранжируют потребительские показатели бронированных автомобилей.

Результаты ранжировки	Номера экспертов							∑R		Rp
Показатели	1	2	3	4	5	6
Степень защищенности	1	2	3	1	1	1	9		1,5
Комплектация	3	3	2	4	5	5	22		3,7
Эргономика	4	5	4	2	3	4	22		3,7
Дизайн	5	4	5	5	4	3	26		4.3
Технический уровень	2	1	1	3	2	2	11		1.8

Средняя сумма рангов = 9+ 22+ 22+ 26+11 / 5 = 18

Отклонение суммы рангов каждого показателя от средней суммы рангов =

9 -18 = -9 , 22-18 = 4, 22 – 18 =4, 26 – 18 = 8, 11 – 18 = -7.

S = (-9²) + (4²) + (4²) + (8²) + (7²) = 226

W = 12* 226 / 6² (5³-5) = 0,628

Определяем границы коэффициента

Результаты ранжировки	Номера экспертов							∑R		Rp
Показатели	1	2	3	4	5	6
Степень защищенности	1	1	1	1	1	1	6		1
Комплектация	3	3	3	3	3	3	18		3
Эргономика	4	4	4	4	4	4	24		4
Дизайн	5	5	5	5	5	5	30		5
Технический уровень	2	2	2	2	2	2	12		2

Средняя сумма рангов = 6 + 18+ 24+30 + 12 / 5 = 18

Отклонение суммы рангов каждого показателя от средней суммы рангов

D₁ = 6 -18 = -12

D₂ = 18 – 18 = 0

D₃ = 24 – 18 = 6

D₄ = 30 – 18 = 12

D₅ = 12 – 18 = -6

S = (-12²) + (0²) + (6²) + (12²) + (-6²) = 144+ 0+36+ 144+ 36 = 360

W = 12* 360 / 6² * (5³ -5) = 4320 / 4320 = 1

Нижняя граница.

Результаты ранжировки	Номера экспертов							∑R		Rp
Показатели	1	2	3	4	5
Степень защищенности	1	2	3	4	5		15		3
Комплектация	2	3	4	5	1		15		3
Эргономика	3	4	5	1	2		15		3
Дизайн	4	5	1	2	3		15		3
Технический уровень	5	1	2	3	4		15		3

W = 0.

Вывод: Значение коэффициента конкордации указывает на уровень связей между мнениями экспертов если W = 1, то согласованность экспертов полная, если W = 0, то результаты экспертизы недостоверны и на основании данных экспертов невозможно сделать каких либо выводов о значимости показателей качества изделия. Если W = 0,6, то это свидетельствует об относительно приемлемой согласованности мнений экспертов.

Для оценки согласованности мнений экспертов, с точки зрения вероятности ошибки экспертного анализа применяют критерий Пирсона.

L²_расч(Лямбда)_. = W*m (l -1)

N(Ню) = l-1

И задаваясь вероятностью ошибки экспертного анализа и числом степеней свободы, сравнивают L_расч с L_табл и делают вывод о вероятности ошибки (A – вероятность) при принятии решений о согласованности мнений экспертов.

	1	2	3	4	5	6	7	8	9	10	11
0.01	6.6	9.2	11.3	13.3	15.1	16.8	18.5	20.1	21.7	23.2	24.7

Если L_расч. Больше L_табл. То с соответствующей A можно утверждать, что согласованность мнений экспертов достаточна.

N=4

L = 15 > 13,3

Вывод: Т.к. 15>13,3 , то с вероятностью ошибки A = 0.01 можно считать что согласованность экспертов достаточна.

Пример №5

На практике возможен случай, когда эксперты вообще не могу присвоить ранг тому или иному показателю. В данном случае для вычисления W делят каждый раз сумму рангов показателя R_i на число равное количеству экспертов принимавших участие в его ранжировании .

Показатели	№ эксперта							∑Ri		Rпр
	1	2	3	4	5	6
Степень защищенности	1	2	3	1	1	1	9		1.5
Комплектация	3	3	2	4	5	5	22		3,7
Эргономика	4	-	4	2	3	4	17		3,4
Дизайн	5	4	-	5	4	3	21		4,2
Технический уровень	2	1	1	3	2	2	11		1,8

1. ∑Ri

2. Rпр = ∑Ri / число экспертов (Mi*)

3. Приведенная средняя сумма рангов T* = 1/L * ∑Riпр = 2,9

4. Приведенное отклонение(D) = Rпр – T*

D1пр = 1,5 – 2,9 = -1,4

D2 = 0,8

D3 = 0.5

D4 = 1.3

D5 = 1.1

5. Сумма отклонений в квадрате = 5,75 (S*)

6. W = 12S / m² (L³ - L) = 12S* / L³ – L = 0,6

Д.з. Пример №6