
- •Гидравлика Методические указания и контрольные задания для студентов заочной формы обучения по специальности 151001 «Технология Машиностроения»
- •Физические свойства жидкостей
- •Основное уравнение гидростатики
- •Давление жидкости на плоские стенки
- •Уравнение Бернулли
- •Истечение жидкости через отверстия, насадки, дроссели и клапаны
- •Гидравлический расчет трубопроводов
Гидравлический расчет трубопроводов
Задача 7.1
Определить,
какое давление должен создавать насос,
перекачивающий воду по горизонтальному
трубопроводу, состоящему из трех
последовательных участков размерами
 ,
если в конечных сечениях участков из
трубопровода отбирается одинаковое
количество воды
,
если в конечных сечениях участков из
трубопровода отбирается одинаковое
количество воды
 ,
а минимальный пьезометрический напор
в конце трубопровода
,
а минимальный пьезометрический напор
в конце трубопровода
 метров водяного столба. Все участки
трубопровода имеют одинаковую
шероховатость
метров водяного столба. Все участки
трубопровода имеют одинаковую
шероховатость
 .
.
|
Исходные данные |
Вариант задания (последняя цифра шифра) |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
||
Исходные данные |
Вариант задания (………… цифра шифра) |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
||
|
400 |
380 |
350 |
370 |
360 |
320 |
300 |
420 |
430 |
450 |
|
|
200 |
210 |
250 |
180 |
200 |
180 |
220 |
200 |
250 |
200 |
|
|
200 |
250 |
280 |
260 |
230 |
200 |
250 |
230 |
210 |
240 |
|
|
150 |
180 |
190 |
160 |
150 |
150 |
180 |
170 |
180 |
150 |
|
|
200 |
250 |
300 |
280 |
150 |
180 |
200 |
250 |
230 |
220 |
|
|
100 |
120 |
140 |
110 |
120 |
100 |
150 |
120 |
130 |
120 |
|
|
10 |
12 |
14 |
15 |
13 |
11 |
10 |
15 |
14 |
16 |
|
|
5 |
6 |
4 |
3 |
5 |
6 |
4 |
7 |
5 |
6 |
|
Задача 7.2
Определить
расход жидкости в каждой ветви сложного
трубопровода, схема которого показана
на рисунке. Диаметры труб всех ветвей
одинаковы и равны
,
длины участков
 .
.
Считать,
что режим течения ламинарный. Местными
потерями пренебречь, суммарный расход
принять
 .
.
|
Исходные данные |
Вариант задания (предпоследняя цифра шифра) |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
||
|
5 |
6 |
7 |
8 |
6 |
4 |
3 |
5 |
4 |
6 |
|
|
3 |
4 |
5 |
6 |
6 |
5 |
4 |
3 |
5 |
4 |
|
|
3 |
5 |
4 |
3 |
2 |
4 |
3 |
3 |
4 |
3 |
|
|
6 |
12 |
14 |
11 |
12 |
10 |
15 |
12 |
13 |
12 |
|
|
10 |
12 |
14 |
15 |
13 |
11 |
10 |
15 |
14 |
16 |
|
Задача 7.3
Насос
обеспечивает расход
 по трубопроводу, в котором установлен
дроссель с коэффициентом сопротивления
по трубопроводу, в котором установлен
дроссель с коэффициентом сопротивления
 .
.
В
точке
 трубопровод разветвляется на два
трубопровода, один из которых содержит
дроссель с коэффициентом сопротивления
трубопровод разветвляется на два
трубопровода, один из которых содержит
дроссель с коэффициентом сопротивления
 ,
а другой имеет дроссель с
,
а другой имеет дроссель с
 .
.
Пренебрегая потерями на трение по длине, определить расходы жидкости в параллельных ветвях и давление, создаваемое насосом.
Диаметр
труб
,
плотность жидкости принять
 .
.
|
Исходные данные |
Вариант задания (третья справа цифра шифра) |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
||
|
0,6 |
0,6 |
0,7 |
0,8 |
0,6 |
0,65 |
0,70 |
0,5 |
0,9 |
0,6 |
|
|
10 |
14 |
15 |
16 |
16 |
15 |
14 |
13 |
15 |
14 |
|
|
40 |
50 |
45 |
35 |
42 |
44 |
53 |
43 |
54 |
40 |
|
|
10 |
12,5 |
25 |
15 |
10 |
14 |
15 |
12 |
13 |
12 |
|
Примеры решения задач
Задача 1.1
При
гидравлическом испытании трубопроводов
внутренних систем водоснабжения
допускается падение давления на
величину .
Определить величину утечки
,
которая приводит к этому падению давления
при гидравлическом испытании системы
объемом
.
Определить величину утечки
,
которая приводит к этому падению давления
при гидравлическом испытании системы
объемом
 .
.
Решение
Изменение
давления и изменение объема занимаемого
жидкостью связаны зависимостью,
определяющей коэффициент объемного
сжатия,
 .
.
При падении давления в трубопроводе на величину объем жидкости в нем должен уменьшиться на величину

Замечание.
Коэффициент объемного сжатия принят
для нормальных условий
 и атмосферном давлении
.
и атмосферном давлении
.
Задача 1.2
Определить
коэффициент температурного расширения
воды, если при увеличении температуры
на
 объем воды равный
объем воды равный
 увеличивается на
увеличивается на
 .
Какой исходной температуре соответствует
полученное значение коэффициента
температурного расширения при давлении
.
.
Какой исходной температуре соответствует
полученное значение коэффициента
температурного расширения при давлении
.
Решение
По определению коэффициент температурного расширения равен
 .
.
По
таблице значений коэффициента
температурного расширения воды от
температуры при
находим, что рассчитанное значение
соответствует температуре от
 (см.[1], стр. 14).
(см.[1], стр. 14).
Задача 1.3
Автоклав
объемом
наполнен жидкостью и закрыт герметически.
Коэффициент температурного расширения
жидкости
 ,
модуль объемной упругости
,
модуль объемной упругости
 .
Определить повышение давления в автоклаве
при увеличении температуры жидкости
на величину
.
Определить повышение давления в автоклаве
при увеличении температуры жидкости
на величину
 .
Объемной деформацией автоклава
пренебречь.
.
Объемной деформацией автоклава
пренебречь.
Решение
При свободном нагреве жидкости на объем жидкости увеличился бы на величину
 .
.
Так
как жидкость не имеет возможности
расширяться, давление в автоклаве будет
увеличиваться. Жидкость подвергнется
сжатию и уменьшит свой объем на
.
Начальный объем следует положить равным
 .
Тогда
.
Тогда
 .
.
Из последней зависимости находим

Задача 2.1
|
К
резервуару с водой подключен
двухжидкостной ртутно-водяной манометр
и технический пружинный манометр.
Определить показания технического
манометра
,
если известны
|
Решение
Последовательно применяя основной закон гидростатики, можно записать:
- давление в сечении 2 пьезометра
 ;
;давление в сечениях 3 и
 пьезометра
пьезометра ;
;давление в сечении 4 пьезометра
 .
.
Записанные равенства позволяют получить уравнение относительно неизвестного давления, регистрируемого манометром

Откуда находим


Задача 2.2
Определить
разность давлений в точках
и
,
находящихся на одном уровне в двух
трубопроводах, заполненных водой, если
разница уровней ртути в дифференциальном
манометре
 .
.
Решение
В поле силы тяжести линия 1-2 принадлежит поверхности постоянного давления. Согласно основному закону гидростатики
|
Аналогично
Очевидно, что
или
|
Из последнего равенства находим

 .
.
Задача 2.3
|
В
закрытом резервуаре находятся две
жидкости: сверху слой воды толщиной
|
Решение
Абсолютное
давление в точке
 резервуара равно
резервуара равно
 ;
;
Из этого равенства следует


 .
.
В
резервуаре абсолютное давление над
поверхностью жидкости меньше атмосферного.
Вакуумметрическое давление
 .
.
Задача 3.1
|
Плоский
затвор перегораживает прямоугольный
канал шириной
|
Решение
Сила гидростатического давления на плоскую стенку площадью находится по формуле
 ,
,
где
 гидростатическое давление в центре
тяжести площади
.
гидростатическое давление в центре
тяжести площади
.
Определяя
силу
 ,
находим
,
находим
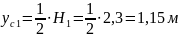 ;
;
 ;
;
 .
.
Расстояние
от свободной поверхности воды до точки
приложения силы
(центра давления
 )
определяется по формуле
)
определяется по формуле
 ,
,
где
 – осевой момент площади
– осевой момент площади
 относительно центральной оси
относительно центральной оси

 .
.
Вычисляем
 .
.
Аналогичные
действия приводят к определению силы
 и точки ее приложения на линии
и точки ее приложения на линии
 :
:
 ;
;
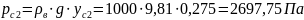 ;
;
 ;
;
 .
.
Равнодействующая
двух параллельных противоположно
направленных сил
 имеет модуль
имеет модуль

Точка
приложения равнодействующей лежит на
линии
и делит отрезок
 на две части обратно пропорциональные
силам
на две части обратно пропорциональные
силам

Из последнего равенства находим

Точка
приложения силы
 практически совпадает с точкой
.
практически совпадает с точкой
.
Задача 3.2
|
Определить
силу давления воды на круглую крышку
люка диаметром
|
Решение
Выберем
систему координат с началом на свободной
поверхности воды и проведем ось
в плоскости перпендикулярной наклонной
стенке так, чтобы она проходила через
центр крышки люка. Ось
 перпендикулярна плоскости рисунка и
совпадает с линией соприкосновения
свободной поверхности воды с наклонной
стенкой.
перпендикулярна плоскости рисунка и
совпадает с линией соприкосновения
свободной поверхности воды с наклонной
стенкой.
Координата центра крышки

Гидростатическое давление в центре крышки находим, используя основной закон гидростатики

Сила давления воды на крышку равна

Точка
приложения силы
 имеет координату
имеет координату
 и расположена ниже центра крышки
и расположена ниже центра крышки

Где – осевой момент круга относительно его центральной оси, параллельной оси .
Задача 3.3
|
Замкнутый
резервуар разделен на две части плоской
перегородкой, имеющей квадратное
отверстие со стороной
Определить
результирующую силу давления на
крышку, если заглубление края отверстия
|
Решение
Абсолютное давление в центре крышки слева


Абсолютное давление на крышку справа (во всех точках его величина имеет одно значение)

Результирующая сила давления на крышку равна

Незначительным
смещением точки приложения силы
 вниз от центра тяжести пренебрегаем.
Равнодействующая сила
проходит через центр крышки.
вниз от центра тяжести пренебрегаем.
Равнодействующая сила
проходит через центр крышки.
Задача 4.1
Определить,
какой вес должен иметь батискаф, чтобы
достигнуть глубины
 при диаметре корпуса
при диаметре корпуса
 и
длине
и
длине
 .
На поверхности плотность морской воды
составляет , температура . Температура
воды на глубине H
-
. Коэффициент объемного сжатия воды ,
коэффициент температурного расширения
воды
.
На поверхности плотность морской воды
составляет , температура . Температура
воды на глубине H
-
. Коэффициент объемного сжатия воды ,
коэффициент температурного расширения
воды
|
Решение
На заданной глубине погружения вес батискафа уравновешивается выталкивающей силой. Выталкивающая сила равна весу воды в объеме, занимаемом батискафом. Эта сила, называемая Архимедовой, определяется по формуле

Объем батискафа без учета деформации корпуса равен

Плотность
воды при температуре
 на глубине
найдем так:
на глубине
найдем так:
уменьшение единицы объема при изменении температуры на
 градусов составит
градусов составит

восемьсот метров глубины погружения увеличат давление на величину

что
уменьшит объем одного кубического метра
воды, находившегося при нормальном
давлении и температуре
 на величину
на величину

Одновременное
изменение температуры и давления
уменьшат объем одного кубометра, имеющего
плотность
 при температуре
при температуре
 на
на

что приведет к повышению плотности до величины

Вес подводной лодки, уравновешенный Архимедовой силой на глубине , должен быть равен

|
Задача 4.2
Прямоугольная
баржа длиной
|
Решение
Принимаем, что плотность воды . Тогда плотность песка по условию задачи равна
 .
.
Выталкивающая сила (Архимедова сила) равна
 .
.
Без учета веса баржи вес загруженного песка равен выталкивающей силе. Значит
 .
.
Тогда толщина слоя песка в барже

Задача 4.3
Объемное
водоизмещение подводной лодки
 .
Для погружения лодки ее отсеки нужно
заполнить морской водой в количестве
.
Для погружения лодки ее отсеки нужно
заполнить морской водой в количестве
 Относительная плотность морской воды
δ
=1,025.
Определить какая часть объема лодки
будет
погружена в воду при и чему равен вес
лодки
Относительная плотность морской воды
δ
=1,025.
Определить какая часть объема лодки
будет
погружена в воду при и чему равен вес
лодки
 при .
при .
Указание. Объемное водоизмещение - объем подводной части судна ниже ватерлинии. При постоянном весовом водоизмещении объемное водоизмещение меняется в зависимости от плотности воды.
|
Решение
Архимедова сила, выталкивающая лодку из воды, при плавании на поверхности равна
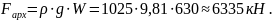
Вес
лодки при нулевом балласте ( )
уравновешен Архимедовой силой,
следовательно
)
уравновешен Архимедовой силой,
следовательно

При погружении лодки ее вес увеличивают на величину веса балластной воды

Полный объем лодки находим из равенства


Часть объема лодки, погруженная в воду при плавании на поверхности, равна

Задача 5.1
Наклонный
трубопровод состоит из четырех участков
с диаметрами
 .
Расход жидкости
.
Расход жидкости
 .
Плотность жидкости . Рассчитать давление
в сечениях 1-1,
2-2, 3-3,4-4,
если давление в сечении 5-5
равно атмосферному, ; ; ; . Потерями напора
пренебречь.
.
Плотность жидкости . Рассчитать давление
в сечениях 1-1,
2-2, 3-3,4-4,
если давление в сечении 5-5
равно атмосферному, ; ; ; . Потерями напора
пренебречь.
Решение
При отсутствии потерь напора (случай течения идеальной жидкости в идеальном канале) удельная энергия на единицу веса жидкости, протекающей через сечение, остается величиной постоянной. Следовательно

При известном расходе жидкости и диаметре поперечного сечения легко найти среднюю скорость течения потока на каждом участке постоянного диаметра

Аналогично
получаем:



Пренебрегая
режимом течения жидкости (он, как правило,
турбулентный), принимаем
 .
.
|
Запишем уравнение Бернулли для сечений 5-5 и 4-4

Так
как
 (это следует из условия
(это следует из условия
 при
при
 ,
находим
,
находим

 .
.
Ясно как найти давление в сечениях 3-3, 2-2, и 1-1:






Расчет показывает, что абсолютное давления по длине канала увеличивается, растет и скорость движения потока. Увеличение давления и скорости происходит за счет потенциальной энергии потока. Геометрический напор уменьшается, а пьезометрический и кинетический напоры растут. Полный напор остается постоянным и равным


Задача 5.2
На
участке трубопровода, состоящего из
труб разного диаметра, к трубе меньшего
диаметра подключен ртутный манометр.
Показание манометра
 .
.
|
Рассчитать
давление и скорость в двух сечениях
разного диаметра, пренебрегая потерями
напора, если известны:
|
Решение
Используя показания жидкостного манометра и основной закон гидростатики, легко найдем избыточное давление в сечении трубы диаметром



При
известном расходе находим среднюю
скорость течения жидкости в сечениях
трубы диаметрами



Запишем уравнение Бернулли для сечений диаметрами , пренебрегая потерями напора

Так
как
 ,
находим избыточное давление в сечении
большего диаметра
,
находим избыточное давление в сечении
большего диаметра

Задача 5.3
|
По трубопроводу постоянного диаметра течет вода. Объемный расход . С помощью ртутного манометра измеряется разность давлений в сечениях, которые расположены на расстоянии друг от друга. Разность высот ртути в трубках манометра . Определить коэффициент трения в формуле Дарси-Вейсбаха.
|
Решение
С
учетом потерь напора на трение на участке
трубопровода
 уравнение Бернулли имеет вид
(предполагается, что режим течения
турбулентный)
уравнение Бернулли имеет вид
(предполагается, что режим течения
турбулентный)

где

– потери напора на преодоление вязкого трения
Так
как
 ,
,
находим
,
,
находим

Давление
в точках
 трубки дифференциального манометра
одинаково. Следовательно
трубки дифференциального манометра
одинаково. Следовательно


Потеря напора на длине равна

Дальнейшие действия очевидны
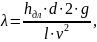
где
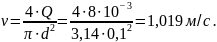

Задача 6.1.
|
Определить
скорость движения поршня под действием
силы
Жидкость считать несжимаемой. При заданном подключении дросселя давление в левой и правой камерах цилиндра одинаково. |
Решение
При постоянной скорости движения поршня сумма проекций всех действующих сил на ось цилиндра равна нулю

Так
как
 ,
находим
,
находим

Если слив жидкости из цилиндра производится при атмосферном давлении, то на дросселе имеет место перепад давления

При таком перепаде давления расход жидкости через дроссель составит

С
другой стороны, – смещение поршня влево
за единицу времени на расстояние
 вытесняет из левой полости объем жидкости
вытесняет из левой полости объем жидкости
 ;
в правой полости цилиндра освобождается
объем
;
в правой полости цилиндра освобождается
объем
 .
Ясно, что
.
Ясно, что
 .Разность
объемов
.Разность
объемов
 определяет объем жидкости, истекающей
через отверстие. Следовательно
определяет объем жидкости, истекающей
через отверстие. Следовательно



При поступательном движении скорость – путь, пройденный телом за единицу времени. Значит

Задача 6.2
|
Определить
скорость перемещения поршня вниз,
если к штоку приложена сила
|
Решение
При постоянной скорости движения поршня силы, действующие на движущиеся части гидроцилиндра, уравновешены. Пренебрегая площадью пяти отверстий в сравнении с площадью поршня, имеем

Следовательно

Пренебрегая давлением столба жидкости над поршнем, определяем объемный расход жидкости через пять отверстий в поршне

Что бы заместить этот объем поршень должен за одну секунду опуститься на метров

откуда следует

Численное значение и есть величина скорости поршня

Задача 6.3
Определить время полного хода поршня гидроцилиндра при движении против нагрузки, если давление на сливе ; давление на входе в дроссель .
|
Нагрузка
вдоль штока
|
Решение
Давление
в левой полости гидроцилиндра найдем
из условия
 ,
что имеет место, когда
,
что имеет место, когда



Перепад давления на дросселе составляет величину

Этот перепад давления обеспечивает объемный расход жидкости через дроссель

При
смещении поршня на величину хода
 освобождается объем в левой полости
цилиндра равный
освобождается объем в левой полости
цилиндра равный

Для заполнения этого объема жидкостью, протекающей через дроссель, потребуется время

Задача 7.1
Определить,
какое давление должен создавать насос,
перекачивающий воду по горизонтальному
трубопроводу, состоящему из трех
последовательных участков размерами
 .
В конечных сечениях участков из
трубопровода отбирается одинаковое
количество воды
.
В конечных сечениях участков из
трубопровода отбирается одинаковое
количество воды
 ,
а минимальный пьезометрический напор
в конце трубопровода
,
а минимальный пьезометрический напор
в конце трубопровода
 водяного столба. Все участки трубопровода
имеют одинаковую шероховатость
.
водяного столба. Все участки трубопровода
имеют одинаковую шероховатость
.
|
Решение
Если
расход на первом участке равен
,
то согласно условию задачи расход на
втором участке составит
 ,
а на третьем -
,
а на третьем -
 .
Условие неразрывности напорного потока
позволяет определить расход жидкости
на первом участке
.
Условие неразрывности напорного потока
позволяет определить расход жидкости
на первом участке

Следовательно,
 ,
,
Давление, создаваемое насосом, должно обеспечить поток жидкости энергией необходимой для движения с требуемой скоростью и преодоления гидравлического сопротивления движению на длине трубопровода. Местными потерями напора на участках смены диаметра трубопровода пренебрежем, т.к. их доля невелика. Для расчета величины потерь на длине необходимо знать скорость течения на каждом участке трубопровода
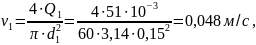


Запишем уравнения Бернулли для сечений 0-0 и 1-1 на первом участке, 1-1 и 2-2 на втором участке, 2-2 и 3-3 на третьем участке



Так как минимальное давление в конечном сечении трубопровода известно

Для
определения
необходимо найти
 ,
,
 ,
,
 .
Общая формула для расчета потерь на
длине имеет вид
.
Общая формула для расчета потерь на
длине имеет вид

где
 - коэффициент гидравлического трения
определяется в зависимости от режима
течения жидкости (от числа
- коэффициент гидравлического трения
определяется в зависимости от режима
течения жидкости (от числа
 и относительной шероховатости трубы
и относительной шероховатости трубы


Рассчитаем значения числа Рейнольдса на участках трубопровода



Для
выбора расчетной формулы для определения
коэффициента
расчитаем для каждого участка отношение




Следуя известным рекомендациям,
Условие |
Расчетная формула |
|
|
|
|
|
|
|
|
находим, что на всех трех участках

Следовательно, режим течения в трубах переходный и расчет производим по формуле

Находим



Выполним расчет потерь напора на длине каждого участка трубопровода:

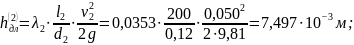

Далее последовательно находим:



Избыточное (манометрическое) давление на выходе из насоса составляет 39428 Па, что составляет ≈0,39 атм; абсолютное давление на выходе из насоса должно составлять 139428 Па или ≈1,39 атм.
|
Качественный график изменения избыточного давления по длине трубопровода показан на рисунке.
Задача 7.2
Определить
расход жидкости в каждой ветви сложного
трубопровода, схема которого показана
на рисунке. Диаметры труб всех ветвей
одинаковы и равны
,
длины участков
 .
.
Считать,
что режим течения ламинарный. Местными
потерями пренебречь, суммарный расход
принять
 .
.
|
Решение
Для определения расходов жидкости в каждой ветви сложного трубопровода можно записать следующие уравнения



Независимыми являются только два первых уравнения. Третье уравнение можно получить, как сумму первого и второго. Следовательно, для решения задачи необходимо составить еще два уравнения.
Обозначим
давление в узлах разветвления трубопровода
 ,
как величины
,
как величины
 – соответственно.
– соответственно.
Очевидно,
что падение давления на линиях
 и
и
 имеет одно значение.
имеет одно значение.


С учетом того, что , находим

Падение
давления между узлами разветвления
трубопровода
 и
и
 определяется расходом жидкости и
гидравлическим сопротивлением линий
определяется расходом жидкости и
гидравлическим сопротивлением линий


что дает еще одно уравнение

Решаем систему уравнений:
Получаем




Задача 7.3
Насос
обеспечивает расход
 по трубопроводу, в котором установлен
дроссель с коэффициентом сопротивления
по трубопроводу, в котором установлен
дроссель с коэффициентом сопротивления
 .
.
В
точке
трубопровод разветвляется на два
трубопровода, один из которых содержит
дроссель с коэффициентом сопротивления
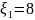 ,
а другой имеет дроссель с
,
а другой имеет дроссель с
 .
.
Пренебрегая потерями на трение по длине, определить расходы жидкости в параллельных ветвях и давление, создаваемое насосом.
Диаметр
труб
 ,
плотность жидкости принять
,
плотность жидкости принять
 .
.
|
Решение
Оценим режим течения в начальной ветви трубопровода, где расход равен .
Скорость течения жидкости

Тогда число Рейнольдса имеет значение

Принимаем
в дальнейших расчетах, что режим течения
в трубах турбулентный, следовательно,
 .
Это заключение будет использоваться
при решении задачи с учетом потерь
напора по длине.
.
Это заключение будет использоваться
при решении задачи с учетом потерь
напора по длине.
Потери напора в простом трубопроводе при заданном расходе жидкости и диаметре трубопровода определяются следующей формулой
.
Так как по условию задачи во внимание принимаются только потери напора на местных сопротивлениях (дросселях), потеря напора на простом трубопроводе определится по формуле
На участке от насоса до разветвления трубопровода потеря давления составит величину

Величины расходов связаны зависимостью

Потери
давления в первой и второй ветвях
трубопровода равны, так как составляют
величину
 ,
что позволяет записать равенство
,
что позволяет записать равенство

Итак,
для определения
 имеем три уравнения:
имеем три уравнения:



Решение
этой системы уравнений при условии
 ,
приводит к результату:
,
приводит к результату:



Вопросы для подготовки к экзамену
Гидростатика
Что такое реальная и идеальная жидкость?
Перечислите основные физические свойства жидкостей и укажите единицы их измерения.
От чего зависит величина кинематической и динамической вязкости и как она определяется?
Что такое гидростатическое давление? Какими свойствами обладает гидростатическое давление?
Приведите основное уравнение гидростатики. Укажите единицы измерения давления.
Как определяется результирующая сила гидростатического давления н а плоскую стенку?
Как определяются составляющие силы гидростатического давления на криволинейную поверхность?
Сформулируйте закон Архимеда.
Перечислите приборы для измерения давления. Как работают пьезометры, манометры, вакуумметры?
Как работает гидравлический пресс?
Литература
Д.В. Штеренлихт, Гидравлика, учебник для ВУЗов, Колос, 2004 г., 656 с.
И.И. Сазанов, Гидравлика, конспект лекций; Москва, МГТУ «Станкин», 2005 г., 190с.
В.А. Кудинов, Э.М. Карташов, Гидравлика, учебное пособие; ВШ, 2008, 199 с.
С.С. Гориславец, Сборник задач с примерами гидравлических расчетов по «Гидростатике», ООО «Изд. Дом «Типография купца Тарасова»», 2007г., 235 с.
С.С. Гориславец, Сборник задач с примерами гидравлических расчетов по «Гидродинамике», ООО «Изд. Дом «Типография купца Тарасова»», 2007г., 364 с.
В.Н. Метревели, Сборник задач по курсу гидравлики с решениями, ВШ, 2008г., 190 с.
Ю.А. Беленков, А.В. Лепешкин, А.А. Михайлин и др., Гидравлика и гидропривод, задачник; Экзамен, Москва, 2009 г., 287 с.
Содержание
|
|
Стр. |
|
Требования к уровню усвоения содержания дисциплины |
3 |
|
Содержание рабочей программы ………………………… |
4 |
|
Выбор задач контрольной работы по темам …………… |
5 |
|
Задачи ………………………………………………………. |
6 |
|
Примеры решения задач ………………………………… |
16 |
|
Вопросы для подготовки к экзамену …………………… |
39 |
|
Литература ………………………………………………….. |
39 |


 ,
м
,
м
 ,
м
,
м
 ,
м
,
м л/с
л/с
 ,
м
,
м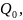 л/с
л/с





 .
. ;
; ;
;
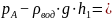
 .
. ,
а под ним слой глицерина. Определить
давление
в резервуаре, если показания пьезометра
,
а под ним слой глицерина. Определить
давление
в резервуаре, если показания пьезометра
 .
. .
Глубина слоя воды до затвора
.
Глубина слоя воды до затвора
 ,
после затвора
,
после затвора
 .
Определить силу гидростатического
давления на затвор и найти точку ее
приложения. Построить эпюру
гидростатического давления по оси
.
.
Определить силу гидростатического
давления на затвор и найти точку ее
приложения. Построить эпюру
гидростатического давления по оси
. ,
закрывающую отверстие в наклонной
стенке. Угол наклона стенки
,
закрывающую отверстие в наклонной
стенке. Угол наклона стенки
 .
Расстояние от уровня свободной
поверхности воды до верхней точки
кромки люка
.
Расстояние от уровня свободной
поверхности воды до верхней точки
кромки люка
 .
Найти точку приложения этой силы и
построить эпюру гидростатического
давления по оси
.
.
Найти точку приложения этой силы и
построить эпюру гидростатического
давления по оси
. ,
закрытое крышкой. Давление на свободной
поверхности жидкости в левой части
резервуара определяется показаниями
манометра
,
закрытое крышкой. Давление на свободной
поверхности жидкости в левой части
резервуара определяется показаниями
манометра
 ,
давление воздуха в правой части
резервуара измеряется мановакуумметром
и равно
,
давление воздуха в правой части
резервуара измеряется мановакуумметром
и равно
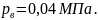
 .
. и шириной
и шириной
 загружена песком ровным слоем высотой
h
.
Осадка баржи с песком
загружена песком ровным слоем высотой
h
.
Осадка баржи с песком
 .
Определить объем песка и высоту слоя
песка h,.
если его относительная плотность δ
= 2.
Массу баржи не учитывать.
.
Определить объем песка и высоту слоя
песка h,.
если его относительная плотность δ
= 2.
Массу баржи не учитывать. ,.
,. .
Известно:
,,
проходное сечение дросселя
.
Известно:
,,
проходное сечение дросселя
 ,
коэффициент расхода дросселя
,
коэффициент расхода дросселя
 .
. .
Поршень диаметром
имеет пять отверстий диаметром
.
Поршень диаметром
имеет пять отверстий диаметром
 .
Отверстия рассматривать как внешние
цилиндрические насадки с коэффициентом
расхода
.
Отверстия рассматривать как внешние
цилиндрические насадки с коэффициентом
расхода
 ,
плотность жидкости, заполняющей
цилиндр, .
,
плотность жидкости, заполняющей
цилиндр, . ,
коэффициент расхода дросселя
,
коэффициент расхода дросселя
 ,
диаметр отверстия дросселя
,
диаметр отверстия дросселя
 ,
плотность масла , диаметр цилиндра ,
диаметр штока , ход штока
,
плотность масла , диаметр цилиндра ,
диаметр штока , ход штока
 .
.






