
Лабораторна робота 2 кореляційний аналіз та дисперсійний аналіз
1. Кореляційний аналіз випадкових величин
1.1 Мета роботи
Вивчити основні етапи кореляційного аналізу випадкових величин.
1.2 Основні положення
При
проведенні кореляційного аналізу
передбачається, що відомі вибірки
реалізацій двох випадкових величин X
та Y,
тобто відомі X![]() і Y
і Y![]() .
.
Коефіцієнт
кореляції
![]() є кількісною мірою лінійної залежності
між двома випадковими величинами X
i Y.
є кількісною мірою лінійної залежності
між двома випадковими величинами X
i Y.
Аналіз діаграм розсіювання дозволяє одержати деяку попередню інформацію про характер зв'язку між випадковими величинами X і Y, тобто про позитивну кореляцію, негативну кореляцію та відсутность кореляційної залежності.
По
вибірках реалізацій випадкових величин
X
і Y
обсягів n
одержують оцінку коефіцієнта кореляції
![]() відповідно до формули:
відповідно до формули:
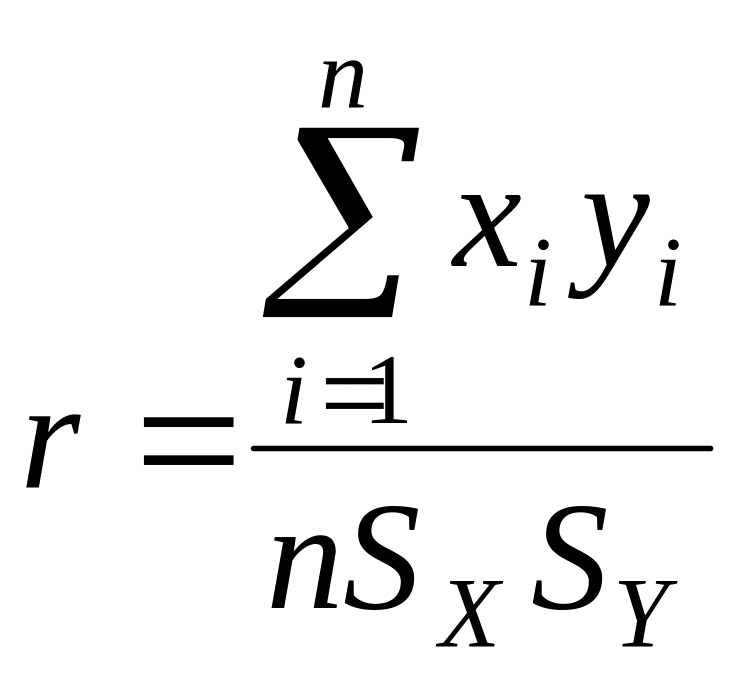 ,
(1.1)
,
(1.1)
де
![]() ;
(1.2)
;
(1.2)
![]() ;
(1.3)
;
(1.3)
![]() ;
(1.4)
;
(1.4)
![]() ;
(1.5)
;
(1.5)
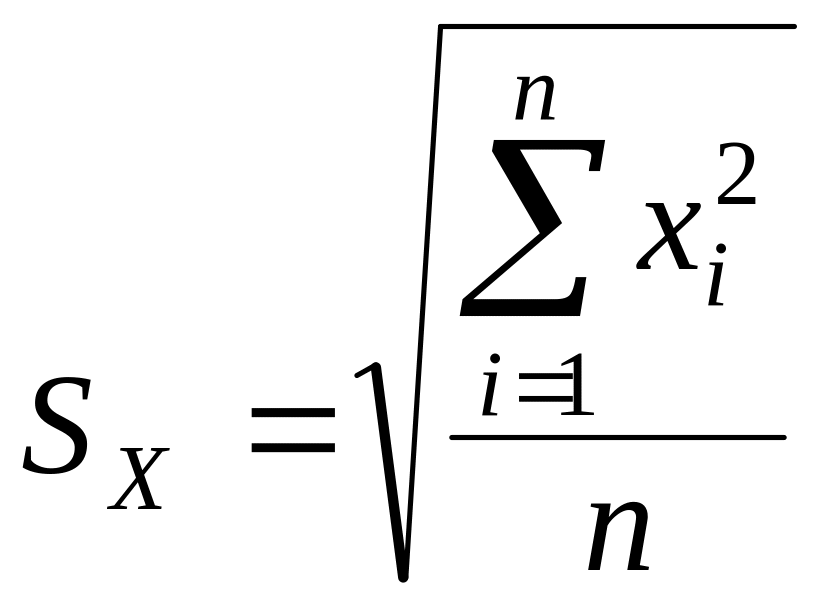 ;
(1.6)
;
(1.6)
 .
(1.7)
.
(1.7)
Оцінка
коефіцієнта кореляції
є випадковою величиною. Тому потрібно
перевірити гіпотезу про значущість
коефіцієнта кореляції, тобто нульову
гіпотезу
![]() проти альтернативної гіпотези
проти альтернативної гіпотези
![]() .
.
За критерій перевірки нульової гіпотези приймають випадкову величину
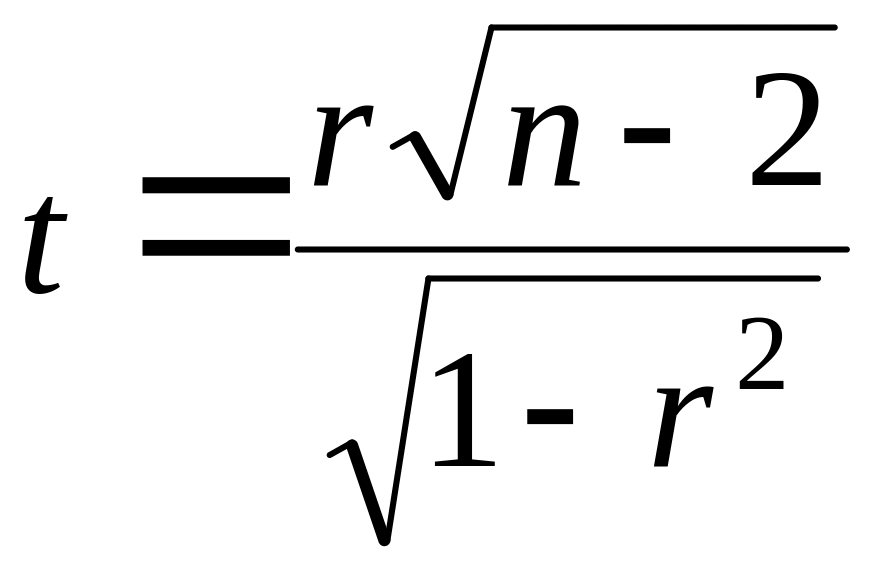 .
(1.8)
.
(1.8)
Величина t при справедливості нульової гіпотези має розподіл Стьюдента з k=n-2 ступенями свободи.
Для того, щоб при заданому рівні значущості a перевірити гіпотезу при альтернативній гіпотезі , необхідно:
1. Обчислити значення критерію, що спостерігається:
![]() .
(1.9)
.
(1.9)
2.
У таблиці критичних точок розподілу
Стьюдента (див. Додаток Б, табл.Б.1) по
заданому рівню значущості a
і числу ступенів свободи k=n-2
знайти критичну точку
![]() для двосторонньої критичної області.
для двосторонньої критичної області.
3.
Зробити порівняння значень
![]() і
і
![]() :
:
-
якщо
![]() <
,
то немає основ відхилити нульову
гіпотезу;
<
,
то немає основ відхилити нульову
гіпотезу;
якщо > , то нульову гіпотезу відхиляють при заданому рівні значущості a.
Перевірка
гіпотези про значущість коефіцієнта
кореляції єквівалентна перевірци
гіпотези про
значущість параметра регресії
![]() ,
тобто є
перевіркою гіпотези
про відсутность лінійного зв'язку.
,
тобто є
перевіркою гіпотези
про відсутность лінійного зв'язку.
На завершальному етапі кореляційного аналізу необхідно дати інтерпретацію отриманим результатам і зробити висновки про характер статистичної залежності між випадковими величинами.
При цьому варто враховувати слідуючі властивості коефіцієнта кореляції.
1. Коефіцієнт кореляції не має розмірності.
2.
Величина
лежить у межах від -1 до +1, тобто
![]() |1|.
Значення
=1
свідчить про те, що між випадковими
величинами X
і Y
існує повна позитивна кореляція -
позитивна лінійна залежність;
|1|.
Значення
=1
свідчить про те, що між випадковими
величинами X
і Y
існує повна позитивна кореляція -
позитивна лінійна залежність;
=-1 указує на повну негативну лінійну залежність;
=0 не означає, що X і Y статистично незалежні, а лише вказує на відсутність лінійного зв'язку між ними.
Таким чином, відмінність коефіцієнта кореляції від нуля означає наявність лінійного стохастичного зв'язку між двома випадковими величинами X і Y тим більш тісного, чим більше за абсолютною величиною значення .
Зв'язок
між оцінкою параметра регресії
![]() і оцінкою коефіцієнта кореляції
і оцінкою коефіцієнта кореляції
![]() має
вигляд:
має
вигляд:
![]() .
(1.10)
.
(1.10)
1.3 Завдання на самостийну роботу
Вивчити метод дослідження стохастичного зв'язку між випадковими величинами за допомогою кореляційного аналізу.
Виписати розрахункові формули для обчислення оцінки коефіцієнта кореляції.
1.4 Порядок виконання роботи
Скласти програму однiєю з алгоритмічних мов та вiдлагодити її.
Зробити
обчислення оцінки коефіцієнта кореляції
і перевірити гіпотезу про значущість
коефіцієнта кореляції, тобто нульову
гіпотезу
![]() при альтернативній гіпотезі
.
при альтернативній гіпотезі
.
На основі аналізу результатів проведеного кореляційного аналізу зробити висновки про наявність або відсутність стохастичної залежності між випадковими величинами X і Y.
Показати, що перевірка гіпотези про значущість коефіцієнта кореляції еквівалентна перевірці гіпотези про значущість параметра регресії .
1.5 Індивідуальні завдання
По вибірках реалізацій випадкових величин X і Y обсягом n=30 зробити кореляційний аналіз.
Вибірка випадкової величини X має загальний вид для усіх варіантів і містить значення:
X={9,8; 15,4; 8,6; 7,6; 10,2; 12,6; 6,6; 10,3; 6,3; 14,8; 11,1; 10,6; 7,3; 12,2; 8,4; 12,7; 7,9; 13,0; 11,5; 13,0; 9,4; 7,2; 11,3; 10,7; 18,5; 13,0; 5,9; 9,3; 10,1; 7,1}.
Вибірки випадкової величини Y для кожного варіанта індивідуального завдання наведені в табл.A.1 (див. Додаток А).
1.6 Контрольні запитання
1. Що таке коефіцієнт кореляції? Які він має властивості?
2. Які існують вигляди кореляційної залежності?
3. За допомогою яких формул обчислюється оцінка коефіцієнта кореляції?
4. Як перевіряється гіпотеза про значущість коефіцієнта кореляції ?
