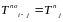- •1. Общие организационно-методические указания
- •2. Задание к экономическому разделу дипломного проекта
- •3. Основные этапы разработки проекта
- •1. Системный анализ 3. Технико-экономические расчеты 5. Реализация проекта 4. Оценка эффективности проекта 2. Проектирование объекта
- •Калькуляция себестоимости древесного угля
- •Показатели экономической эффективности:
- •4. Сетевое планирование разработки проекта
- •Формулы для расчета модели
- •Расчет параметров сетевого графика
- •Фрагмент таблицы основных событий и работ проекта
- •5. Календарный график выполнения проекта
- •6. Структура затрат на выполнение проекта
- •Единовременные затраты;
- •Текущие затраты.
- •Тарифы страховых взносов
- •7. Методы оценки эффективности инвестиций
- •1. Метод чистой текущей стоимости
- •2 Метод внутренней ставки дохода
- •3. Метод периода окупаемости
- •4. Метод индекса прибыльности
- •5. Метод расчета коэффициента эффективности инвестиции
- •8. Прогнозирование прибыли
- •Экономические показатели по разработке и реализации проекта
- •I этап (4 месяца)
- •II этап (4 месяца)
- •III и IV этапы (по 4 месяца каждый)
- •V этап (все последующие годы)
- •Экономическая оценка инвестиций
- •Исходные данные для выполнения проекта
- •I.Затраты на приобретение оборудования
- •II. Расчет срока окупаемости
- •2. Определение затрат:
- •2.1. Зарплата
- •2.2. Затраты на материалы и покупные комплектующие изделия
- •2.3. Общехозяйственные и общепроизводственные расходы
- •2.3. Затраты на оборудование
- •Чистая прибыль:
- •3.1. Определим прибыль от реализации услуг автосервиса по формуле:
- •3.2. Чистая прибыль определяется по формуле:
- •4. Определение требуемых инвестиций:
- •5.Чистый доход:
- •6. Определение эффективности инвестиций методом чистого дисконтированного дохода:
- •Результаты расчета чдд и чтс
- •Пример №2
- •10.2 Экономическая оценка проекта по реконструкции агрегатного участка
- •Расчет потребности в капитальных вложениях
- •Стоимость основного оборудования
- •Стоимость инвентаря агрегатного участка
- •Расчет затрат
- •1. Расчет расходов на оплату труда
- •2. Расчет страховых взносов
- •Тарифы страховых взносов
- •3. Амортизация основных фондов
- •4. Затраты на запасные части и материалы
- •Затраты на запасные части и материалы
- •5. Цеховые расходы участка
- •6. Смета затрат и калькуляция себестоимости
- •Смета затрат и калькуляция себестоимости
- •Определение цены одного чел.-ч работ ремонтных и выручки:
- •III. Расчет сводных показателей экономической эффективности
- •1. Расчет прибыли
- •2. Расчет чистой прибыли
- •3. Расчет рентабельности
- •4. Расчет фондоемкости и фондоотдачи
- •5. Экономическая эффективность
- •6. Срок окупаемости капитальных вложений
- •Результаты работы предприятия
- •IV. Расчет критического объема работ для агрегатного участка
- •Пример № 3
- •10.3 Экономическое обоснование проекта линии инструментального контроля амтс на Учебно-Экспериментальной Базе мгту
- •1. Технико-экономическое обоснование проекта
- •2. Описание проектируемой системы
- •Технико-экономические показатели проекта
- •3. Первоначальные капиталовложения
- •Стоимость приобретенных основных средств
- •Оборудование для офиса
- •Дополнительные расходы
- •4. Расчет суммы выручки
- •5. Расчет затрат
- •5.1. Сумма отчислений гибдд
- •5.2. Расчет расходов на оплату труда
- •Расходы на оплату труда
- •5.3. Расчет страховых взносов
- •Тарифы страховых взносов
- •Ежегодные затраты страховых взносов
- •5.4. Затраты на коммунальные платежи
- •3Атраты на коммунальные платежи
- •5.5. Амортизационные отчисления
- •3Атраты на амортизационные отчисления
- •5.6. Смета затрат и калькуляция себестоимости
- •Смета затрат и калькуляция себестоимости
- •6.1. Расчет прибыли
- •6.2. Расчет чистой прибыли
- •6.3. Расчет чистого дохода
- •6.4. Расчет рентабельности
- •Результаты расчета чдд и чтс
- •Пример 4
- •Рекомендуемая литература:
- •Тарифы - 2014
- •Электрическая энергия
- •Установлены тарифы на электрическую энергию для населения Мурманской области,
- •Тепловая энергия
- •Тарифы на тепловую энергию для потребителей
- •Водоснабжение и водоотведение
- •Ставки налогов в 2015 году не изменились!!! Ставка ндс в 2014 году.
- •Ставки налогов в 2014 году при применении специальных налоговых режимов:
- •Ставки страховых взносов в 2014 году
Формулы для расчета модели
Таблица 1
Наименование параметров |
Расчетная формула |
Условные обозначения |
Раннее начало работы |
|
Tpнi-j – раннее начало работы; Tpi – раннее совершение события |
Раннее окончание работы |
|
Tpоi-j – раннее окончание; ti-j – продолжительность работы |
Позднее начало работы |
|
Tпнi-j – позднее начало работы |
Позднее окончание работы |
|
Tnoi-j – позднее окончание работы; Тnj – позднее совершение работы |
Полный резерв времени работы |
|
Rnij – полный резерв времени работы |
Полный резерв времени пути |
|
R(Li) – полный резерв времени пути; t(Lкр) - продолжительность критического пути; t(Li) – продолжительность анализируемого пути |
Если сроки выполнения всех работ не укладываются в директивные, необходимо произвести оптимизацию сети. В этих целях можно, во-первых, увеличить количество исполнителей, во-вторых, произвести перераспределение трудовых ресурсов путем переключения части работников с работ, имеющих большие резервы времени, на выполнение работ, лежащих на критическом пути. Сетевой график приведен на рис. 3.

Рис. 3 – Сетевой график для комплекса проектно-конструкторских работ
Каждый путь имеет свойственные ему сроки выполнения работ:
0-1 – 21 день; 1-2 – 26 дней; 1-3 – 26 дней; 1-5 – 35 дней; 2-4 – 7 дней; 3-9 – 14 дней; 3-10 – 21 день; 4-5 – 7 дней; 4-8 – 14 дней; 4-11 – 42 дня; 5-6 – 49 дней; 6-7 – 35 дней; 7-11 – 70 дней; 10-11 – 14 дней; 10-13 – 14 дней; 11-12 – 42 дня; 12-13 – 49 дней.
Важной задачей является определение количества времени, необходимого для выполнения всех работ сетевого графика. Если известны нормативы трудоемкости конструкторских и проектных работ и рассчитана численность занятых в них работников, продолжительность каждой работы устанавливается по формуле определения длительности цикла отдельных работ. Если нормативы отсутствуют, от руководителя или ответственного исполнителя работы получают минимальную tmin, максимальную tmax и наиболее вероятную tнв оценки времени. Эти величины являются исходными для расчета ожидаемого времени tож, которое представляет собой математическое ожидание случайной величины, в данном случае продолжительности работ.
Для более полной характеристики распределения случайной величины используется понятие дисперсии. Если дисперсия невелика, то имеется большая уверенность относительно момента завершения данной работы.
При принятом в системе сетевого планирования законе β-распределения:
 (4)
(4)
 (5)
(5)
 (6)
(6)
Данные расчета параметров сети рекомендуется сводить в таблицу (табл. 2). Расчеты основных параметров сетевого графика могут быть выполнены с применением электронно-вычислительной техники.