4.4. Теорема об изменении кинетической энергии.

4.4.1. Работа постоянной силы.

Рассмотрим сначала вычисление работы силы в весьма частном случае. Пусть на материальную точку действует сила , постоянная по величине и направлению, и эта точка приложения силы перемещается прямолинейно из положения в положение (рис. 35).

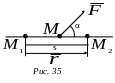В рассматриваемом случае работой силы называется произведение модуля силы на перемещение её точки приложения и на косинус угла между направлением вектора силы и направлением перемещения точки приложения силы, т. е.

.

Если угол острый, то работа силы , а если тупой, то .

Если направления вектора силы и перемещения её точки приложения совпадают, т. е. , то .

Если направление вектора силы перпендикулярно перемещению её точки приложения, т. е. , то .

Если направление вектора силы противоположно направлению перемещения её точки приложения, то

4.4.2. Элементарная работа силы.

Пусть сила переменна как по величине, так и по направлению, а её точка

приложения (материальная точка ) перемещается по криволинейной траектории (рис.36).

Вычислим работу силы на элементарном участке —элементарном перемещении точки приложения силы . Этот участок можно считать прямолинейным, тогда вектор элементарного перемещения точки , направлен по касательной к траектории в сторону движения точки и по величине . Кроме того, можно считать, что сила на рассматриваем элементарном участке постоянна по величине и направлению.

Определение. Элементарной работой силы называется произведение модуля силы на элементарное перемещение её точки приложения и на косинус угла между вектором силы и вектором элементарного перемещения , т. е.

.

Элементарную работу можно также записать в виде

Элементарную работу обозначают , а не , так как в общем случае она не является дифференциалом функции.

Если силу и вектор элементарного перемещения разложить по осям

к оординат (рис.37), то

, .

Подставляя в (4.59) значения и ,получаем формулу для элементарной работы в проекциях на оси координат

.

Элементарная работа силы равна сумме произведения проекций этой силы на оси координат на дифференциалы соответствующих координат точки приложения силы.

4.4.3. Работа силы на конечном перемещении.

Определим работу силы на конечном перемещении её точки приложения из положения в положение .Для этого разобьем это перемещение на перемещений, каждое из которых в пределе—элементарное. Тогда работа может быть выражена как

,

где —работа силы на -ом элементарном перемещении, на которые разбито полное перемещение. Так как сумма в этом выражении для работы является интегральной суммой, то работа силы на конечном перемещении её точки приложения выражается криволинейным интегралом:

= .

Теорема (о работе равнодействующей). Работа равнодействующей системы сил на каком либо перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.

Теорема(о работе силы на последовательных перемещениях).Работа силы на конечном перемещении равна сумме работ этой же силы на последовательных составляющих перемещениях, на которые любым образом разбито исходное конечное перемещение.

Доказательство следует из возможности разбиения любым образом всего промежутка интегрирования на составляющие, причем интеграл по всему промежутку интегрирования равен сумме интегралов по составляющим.

Наряду с понятием работы вводят также понятие мощности.

Мощностью силы называется отношение элементарной работы к элементарному промежутку времени, за который она совершена

.

Если учесть, что , то

,

т. е. мощность равна скалярному произведению силы на скорость.

За единицу работы в СИ принимают джоуль: 1 Дж=1 Н·м, за единицу мощности ватт: 1 Вт=1 Дж/с.

4.4.4. Работа силы тяжести.

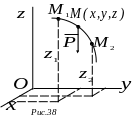Пусть точка , на которую действует сила тяжести , переместилась из положения в положение (рис.38).

Вычислим работу силы . Вблизи поверхности Земли силу тяжести можно считать постоянной и направленной по вертикали вниз. Ее проекции на оси координат

, . Элементарная работа—формула (4.61):

Работа силы на перемещении :

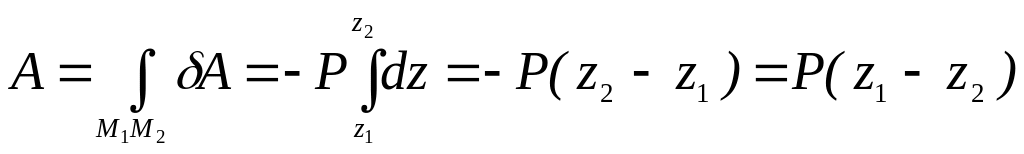
Окончательно

,

где — падение высоты.

Работа силы тяжести равна произведению силы тяжести на падение высоты ее точки приложения. Если точка приложения силы тяжести опускается , то работа положительная, если поднимается —отрицательная.

Работа силы тяжести не зависит от формы траектории ее точки приложения, а зависит только от начального и конечного положений этой точки приложения.