4.3.3. Законы сохранения кинетического момента

(следствия из теоремы)

Следствие 1. Если главный момент внешних сил системы относительно неподвижного полюса равен нулю, то кинетический момент этой системы относительно того же полюса будет постоянным как по величине, так и по направлению.

Действительно, на основании (4.22) имеем: . Если , то .

Следствие 2. Если главный момент внешних сил системы относительно неподвижной оси равен нулю, то кинетический момент этой системы относительно той же оси будет постоянным.

Если , тогда по формуле (4.27): и .

4.3.4. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси, относительно оси вращения.

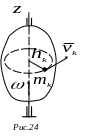Рассмотрим твердое тело, вращающееся вокруг неподвижной оси с угловой скоростью (рис.24). Кинетический момент материальной точки

массы относительно оси (формула (4.18)):

.

Учитывая, что , где —алгебраическая угловая скорость тела:

.

Кинетический момент тела относительно оси будет, согласно (4.20), равен алгебраической сумме этих выражений для всех точек тела

Определение. Моментом инерции твердого тела (механической системы) относительно оси называется сумма произведений масс всех точек тела (системы) на квадрат их расстояний от этой оси, т. е.

Размерность момента инерции в системе СИ—кг·м². Часто при вычислениях применяют понятие радиуса инерции. Радиусом инерции тела относительно оси называется величина , определяемая равенством

,

где —масса тела.

Возвращаясь к формуле (4.32), получаем

,

т. е. кинетический момент твердого тела, вращающегося вокруг неподвижной оси, относительно оси вращения равен произведению момента инерции тела относительно оси вращения на алгебраическую угловую скорость этого тела.

Теорема. Момент инерции механической системы относительно некоторой оси равен моменту инерции относительно параллельной оси , проходящей через центр масс системы, сложенному с произведением массы системы на квадрат расстояния между осями, т. е.

. (4.41)

1. Тонкий однородный стержень длиной и массой . Вычислим его момент инерции относительно симметрии (рис. 28).

Направим вдоль оси стержня координатную ось . Для любого элементарного отрезка длины величина , масса , где —масса единицы длины стержня (линейная плотность). В соответствии с формулой (4.42)

.

Окончательно

.

2 . Тонкое круглое однородное кольцо радиуса и массы . Вычислим момент инерции относительно оси , перпендикулярной плоскости кольца и проходящей через его центр (рис.29).

Так как все точки кольца находятся от оси на расстоянии , то по формуле (4.33):

.

Окончательно

.

3 . Круглая однородная пластина или цилиндр радиуса и массой .

Вычислим момент инерции круглой однородной пластины относительно оси , перпендикулярной пластине и проходящей через ее центр (рис.30). Для этого выделим элементарное кольцо радиусом и шириной . Площадь этого кольца , а масса , где —масса единицы площади пластины. Тогда по формуле (4.44) для выделенного элементарного кольца

,

а для всей пластины

.

Заменяя его значением, получим окончательно

.

Такая же формула получится и для момента инерции однородного круглого цилиндра массой и радиусом относительно его оси (рис.31). Для доказательства этого разобьем цилиндр на элементарные пластины массой . Момент инерции каждой из этих пластин относительно оси определяется формулой (4.45):

.

Момент инерции цилиндра относительно оси равен сумме моментов инерции всех элементарных пластин относительно той же оси, т. е.

.