3.3 Дифференциальные уравнения движения механической системы.
Рассмотрим
механическую систему, состоящую из
материальных точек, массы которых
.
Для каждой точки
применим основное уравнение динамики
точки
, 
,
или
,
где —равнодействующая внешних сил, приложенная к -ой точке, а —равнодействующая внутренних сил.
Систему дифференциальных уравнений (3.3) называют дифференциальными уравнениями движения механической системы в векторной форме.
Проектируя векторные уравнения (3.3) на прямоугольные декартовые оси координат получим дифференциальные уравнения движения механической системы в координатной форме:
,
,
,
Эти
уравнение представляют собой систему
обыкновенных дифференциальных уравнений
второго порядка. Следовательно, для
нахождения движения механической
системы по заданным силам и начальным
условиям для каждой точки этой системы,
необходимо проинтегрировать систему
дифференциальных уравнений. Интегрирование
системы дифференциальных уравнений
(3.4), вообще говоря, сопряжено со
значительными, зачастую непреодолимыми
математическими трудностями. Однако в
теоретической механике разработаны
методы, которые позволяют обойти основные
трудности, возникающие при использовании
дифференциальных уравнений движения
механической системы в форме (3.3) или
(3.4). К их числу относятся методы, которые
дают общие теоремы динамики механической
системы, устанавливающие законы изменения
некоторых суммарных (интегральных)
характеристик системы в целом, а не
закономерности движения отдельных её
элементов. Это так называемые меры
движения—главный вектор количества
движения; главный момент количества
движения; кинетическая энергия. Зная
характер изменения этих величин, удается
составить частичное, а иногда и полное
представление о движении механической
системы.
IV. Основные (общие) теоремы динамики точки и системы
4 .1 Теорема о движении центра масс.
4.1.1.Центр масс механической системы.
Рассмотрим механическую систему, состоящую из материальных точек, массы которых .
Массой механической системы, состоящей из материальных точек, будем называть сумму масс точек системы:
.
Определение.
Центром масс механической системы
называется геометрическая точка
,
радиус вектор которой определяется по
формуле:
,
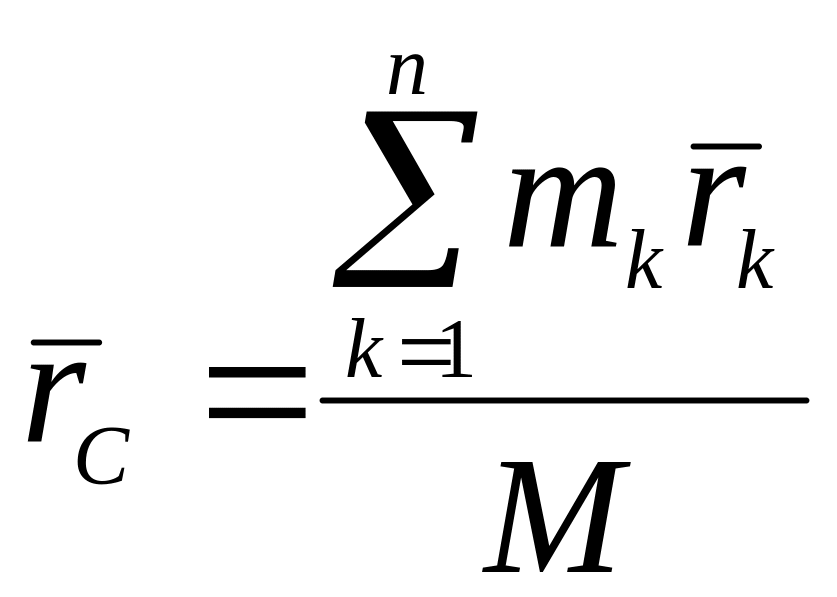где
—радиус-вектор
центра масс;
—радиус-векторы
точек системы;
—их
массы (рис.18).
Проецируя (4.1) на декартовые оси координат получим формулы для координат центра масс
; 
; 
.
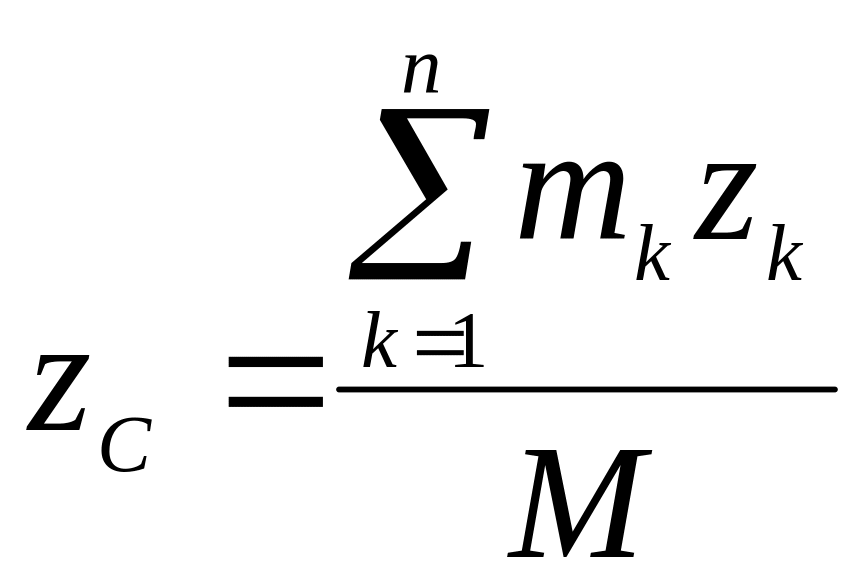Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой механической системы. В однородном поле силы тяжести центр масс совпадает с центром тяжести. Это, однако, не означает, что понятия центра масс и центра тяжести одинаковы. Понятие центра масс применимо к любым механическим системам, а понятие центра тяжести применимо только к механическим системам, находящимся под действием сил тяжести (то есть притяжения к Земле). Так, например, в небесной механике при рассмотрении задачи о движении двух тел, например Земли и Луны, можно рассматривать центр масс этой системы, но нельзя рассматривать центр тяжести.
Таким образом, понятие центра масс более широкое, чем понятие центра тяжести.