III. Введение в динамику механической системы.
3.1 Механическая система. Силы внешние и внутренние.
Механической системой называется такая совокупность материальных точек или тел, в которой положение или движение каждой точки или тела зависит от положения и движения всех остальных. Так, например, при изучении движения Земли и Луны относительно Солнца совокупность Земли и Луны является механической системой, состоящей из двух материальных точек, при разрыве снаряда на осколки мы рассматриваем осколки как механическую систему. Механической системой является любой механизм или машина.
Если расстояния между точками механической системы не изменяются при движении или покое системы, то такая механическая система называется неизменяемой.
Понятие неизменяемой механической системы позволяет изучать в динамике произвольное движение твердых тел. При этом, как в статике и кинематике, под твердым телом будем понимать такое материальное тело, у которого расстояния между каждыми двумя точками не изменяется при движении или покое тела. Любое твердое тело можно мысленно разбить на достаточно большое число достаточно малых частей, совокупность которых можно приближенно рассматривать как механическую систему. Так как твердое тело образует непрерывную протяженность, то для установления его точных (а не приближенных) свойств необходимо совершить предельный переход, предельное дробление тела, когда размеры рассматриваемых частей тела одновременно стремятся к нулю.
Таким образом, знание законов движения механических систем позволяет изучать законы произвольных движений твердых тел.
Все силы, действующие на точки механической системы, разделяют на внешние и внутренние силы.
Внешними
силами по отношению к данной механической
системе называются силы, действующие
на точки этой системы со стороны
материальных точек или тел, не входящих
в систему.
Обозначения:
—внешняя
сила, приложенная к
-ой
точке;
—главный
вектор внешних сил;
—главный
момент внешних сил относительно полюса.
Внутренними
силами называются силы, с которыми
материальные точки или тела, входящие
в данную механическую систему, действуют
на точки или тела этой же системы.
Другими словами, внутренние силы–это
силы взаимодействия между точками или
телами данной механической системы.
Обозначения:
—внутренняя
сила, приложенная к
-ой
точке;
—главный
вектор внутренних сил;
—главный
момент внутренних сил относительно
полюса.
3.2 Свойства внутренних сил.
Первое свойство. Главный вектор всех внутренних сил механической системы равен нулю, то есть
.
Второе свойство. Главный момент всех внутренних сил механической системы относительно любого полюса или оси равен нулю, то есть
, 
.
Для
доказательства этих свойств заметим,
что, так как внутренние силы—это силы
взаимодействия материальных точек,
входящих в систему, то по третьему закону
Ньютона любые две точки системы (рис.
17) действуют друг на друга с силами
и
,
равными по модулю и противоположными
по направлению.
Т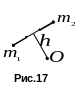
аким
образом, для каждой внутренней силы
имеется прямопротивоположная внутренняя
сила и, следовательно, внутренние силы
образуют некоторое множество попарно
противоположных сил. Но геометрическая
сумма двух прямо противоположных сил
равна нулю, поэтому
.
Как было показано в статике, геометрическая сумма моментов двух прямо противоположных сил относительно одного и того же полюса равна нулю, поэтому
.
Аналогичный результат получается и при вычислении главного момента относительно оси
.