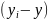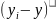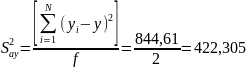5.1 Алгоритм планирования эксперимента

1. Выбор параметра оптимизации, вида функции отклика, факторов и их уровней.

2. Формирование матрицы планирования, способа дублирования опытов.

3. Рандомизация опытов.

4. Проведение опытов, заполнение столбцов результатов «y» в матрице планирования.

5. Оценка коэффициента линейной модели.

6. Нахождение дисперсии «y»; S_y² и дисперсии коэффициентов S_b².

7. Определение значимости коэффициентов линейной модели, используя их доверительные интервалы. Удаление слагаемых линейной модели с незначимыми коэффициентами.

8. Нахождение дисперсии адекватности, критерия Фишера и проверка адекватности модели.

9. Переход к модели более высокого порядка, если линейная модель неадекватна, дополнение матрицы планирования, проведение дополнительных опытов и расчет модели второго порядка. [1, c. 129].

5.2 Пример планирования эксперимента

Требуется установить влияние заднего угла α, переднего угла γ, главного угла в плане φ, вспомогательного угла в плане φ1, радиуса при вершине r на стойкость Т токарного резца.

Выбираются основные уровни факторов: α = 6° – 10°; γ = 2° – 9°; φ = 39° – 45°; φ1 = 20° – 25°; r = 0,2 – 0,8. Основной уровень i-го фактора и интервал варьирования на уровне рассчитываются по формулам:

x_oi=(x_imax+ x_imin)/2; ε_oi=(x_imax - x_imin)/2

(табл. 10 ).

Таблица 10 - Уровни и интервалы варьирования факторов

Факторы	Кодовое значение	Интервал варьирования	Уровни факторов
			Верхний +1	Основной 0	Нижний -1
γ	X1	3.5°	-2°	-5.5°	-9°
α	X2	2°	10°	8°	6°
φ	X3	2.5°	25°	22.5°	20°
φ1	X4	3°	45°	42°	39°
r	X5	0.3°	0.8°	0.5°	0.2°

На 1-ом этапе исследования в качестве плана эксперимента принимаем ¼ реплику ( ) от полного факторного эксперимента . Реплика задана генерирующим соотношением X₄ = Х₁Х₂; Х₅ = Х₁Х₂Х₃. Матрица планирования и результатов опытов (табл. 11) проведения представлена в табл. 12.

Таблица 11 – Исходные данные

Значения стойкости резцов, полученные в результате эксперимента, Т (мин)
29,5	30,1	28,8	27,0	30,0	28,5	29,0	31,2
Значение параметра оптимизации уи в u-ом опыте
24,1		23,6		23,9		24,0

Таблица 12 - Матрица планирования эксперимента

N	X0	X1	X2	X3	X4	X5	У(T), мин
1	+	+	+	+	+	+	29,5
2	+	-	+	+	-	-	30,1
3	+	+	-	+	-	-	28,8
4	+	-	-	-	+	-	27,0
5	+	+	+	-	+	-	30,0
6	+	-	+	-	-	+	28,5
7	+	+	-	+	-	-	29,0
8	+	-	-	+	+	+	31,2

Для описания используем линейную модель вида:

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₄x₄ + b₅x₅; b₀ = x₅x₀; b₁ = x₅x₁ (6)

Значение коэффициента b_{i =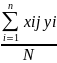} (7)

b_{0 = 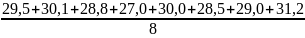= 29,263}

b_{1 = 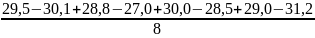= 0,063}

b_{2 = = 0,263}

b_{3 = = 7,888}

b_{4 = = 0,163}

b_{5 = = -6,963}

y = 29,263+0,063х₁+0,263х₂+7,888х₃+0,163х₄-6,963х₅.

Дисперсию параметра оптимизации вычисляем по результатам четырёх опытов в центре плана, т.е. при x₁ = x₂ = x₃ = x₄ = 0. Расчёт дисперсии

приведён в табл. 13.

Таблица 13 - Таблица расчёта дисперсии

N	yi	y
1	24,1	23,9	0,2	0,04
2	23,6		-0,3	0,09
3	23,9		0	0,0
4	24,0		0,1	0,01
Ʃ	95,6			0,14

n0 – число опытов в центре плана; y_i – значение параметра оптимизации в i-ом опыте в центре плана.

= / N = 0, 0467/8 = 0, 0058.

Доверительный интервал Δb_i = ±iS_bi , Δb – условие выполнятся для всех b_i.

y = 29,263 + 0,063x₁ + 0,263x₂ + 7,888x₃ + 0,163x₄ – 6,963x₅. (9.1)

Для проверки гипотезы адекватности модели, представленной уравнением (9.1), находим дисперсию адекватности

(8)

где y– значение параметра оптимизации в i-ом опыте, вычисленное по уравнению регрессии; f = N – (k – 1) – число степеней свободы; k – число факторов.

Расчёт дисперсии приведён в табл. 14.

Таблица 14 - Таблица расчёта дисперсии

N	yi	yi
1	29,5	30,7	-1,2	1,44
2	30,1	44,2	-14,1	198,81
3	28,8	43,8	-15	225
4	27,0	28,2	-1,2	1,44
5	30,0	28,8	1,2	1,44
6	28,5	14,5	14	196
7	29,0	43,8	-14,8	219,04
8	31,2	30,0	1,2	1,44
Ʃ				844,61

Проверка гипотезы адекватности проводится по F-критерию Фишера. Для этого найдём F_{p = /} = 422,305 /0,0467 = 9042,9

Если F_p < F_т – модель адекватна. В нашем случае 9042,9 > 9,55, условие не выполняется и модель неадекватна. [4, c 165-169].

Заключение

Проверив на практике методы оптимизации и методы решения транспортных задач, я подтвердил эффективность их применения в решении конкретных инженерных вопросов. При решении транспортной задачи методом Фогеля, я также увидел его эффективность, что это наиболее эффективный метод решения данных задач и он позволяет найти максимально приближенный к оптимальному опорный план.

Попробовал провести планирование эксперимента согласно алгоритма, рассмотрел влияние углов токарного резца на его стойкость.

Список литературы

1. Потапов Б.Ф. Начала инженерного творчества: учеб. пособие / Перм. гос. техн. ун-т. – Пермь, 2010. – 190 с.

2. Интернет – ресурс Федерального института промышленной собственности (ФИПС) - http://www1.fips.ru/.

3. Бедарев И.А.Численные методы решения инженерных задач в пакете MathCad: учеб. пособие / Новосиб. гос. архитект. – строит. ун-т. – Новосибирск, 2005. – 98 с.

4. Ванин, В.А. Научные исследования в технологии машиностроения: учеб. пособие/ Тамб. гос. техн. ун-т. – Тамбов, 2009. – 232 с.

28