Содержание

Реферат..………………………………………………………………………………………3

Введение………………………………………………………………………………………3

1 Описание изобретения …………………………………………………………………….4

1.1 Область использования………………………………………………………………….4

1.2 Цель изобретения……..………………………………………………………………….4

1.3 Сущность изобретения и отличительные от прототипа признаки………………..…5

1.4 Пример конкретного выполнения………………………………………………………5

2 Одномерная оптимизация…………………………………………………………………6

3 Многомерная безусловная градиентная оптимизация…………………………………..8

3.1 Метод градиента…………………………………………………………………………8

3.2 Метод Гаусса-Зайделя………………………………………………………………….18

4 Решение транспортной задачи методом Фогеля………………………………………..20

5 Планирование эксперимента…………………………………………………………… 24

5.1 Алгоритм планирования эксперимента……………………………………………….24

5.2 Пример планирования эксперимента………………………………………………….25

Заключение………………………………………………………………………………….27

Список литературы…………………………………………………………………………28

Отчет 28 с., 4 рис., 14 табл.

Реферат

Цель работы – научиться правильно описать изобретение, научиться решать задачи одномерной и двумерной оптимизации, а также решать транспортную задачу методом Фогеля, который позволяет найти опорный план максимально приближенный к лучшему.

В отчете выполнено описание изобретения с помощью сайта ФИПС. Оттуда взято изобретение и расписано в работе. Решены задачи по одномерной оптимизации и многомерной оптимизации методом градиента и Гаусса – Зайделя. Также решена транспортная задача методом Фогеля.

Введение

Курс «Начала (основы) инженерного творчества» входит в учебные планы практически всех специальностей технического профиля. При этом названия дисциплин отличаются от упомянутого только конкретизацией предметной области. Указанная дисциплина изучается, как правило, на третьем курсе. На этом этапе обучения студенты представляют направление инженерной деятельности, в котором они будут специализироваться, изучив «Введение в специальность» .

В данном отчете рассмотрены такие темы как изобретательство. Мной выбран пример изобретения – это сверло с регулируемым диаметром резания, что позволяет снизить номенклатуру покупного инструмента и тем самым снизить себестоимость детали. Также рассмотрены методы оптимизации которые позволяют найти пусть не лучший, но максимально приближенный к лучшему результат, за достаточно короткий промежуток времени. [1, c. 5]

1 Описание изобретения

Сверло с устройствами регулировки диаметра резания.

Код по международной патентной классификации: B23B51.

Автор(ы): Огоньков Константин Эдуардович (RU)

Патентообладатель(и): Огоньков Константин Эдуардович (RU)

Дата публикации: 27 мая 2012 года.

Дата начала действия патента: 22 июня 2010 года [2].

1.1 Область использования:

Изобретение относится к обработке материалов резанием. Более конкретно – к сверлам, и может использоваться для сверления отверстий в прокате, в поковках из стали, обработке отливок из цветных металлов. Также может использоваться в обработке заготовок из пластмасс [2].

1.2 Цель изобретения:

Цель данного изобретения в том чтобы уменьшить номенклатуру режущего инструмента данного типа, путем изменения диаметров обрабатываемого отверстия, тем самым уменьшить затраты на покупку или изготовление отдельного сверла на каждое отверстие [2].

1.3 Сущность изобретения и отличительные от прототипа признаки:

Указанный технический результат достигается тем, что данное сверло содержит корпус, в котором размещен регулируемый элемент, регулировочную пластину, которая взаимодействует с регулируемым элементом через регулировочный винт. Также имеются фиксирующие винты, для закрепления данных регулировочных элементов. От прототипа отличает то, что данное сверло позволяет настраивать диаметр сверления в определенном диапазоне (в зависимости от того, с каким базовым диаметром выполнен корпус) [2].

1.4 Пример конкретного выполнения (рисунок 1):

Рисунок 1 – пример конкретного выполнения сверла

Сверло содержит корпус (1), регулируемый элемент (2), регулировочную пластину (4), имеющую боковую поверхность для взаимодействия с регулируемым элементом, регулировочный винт (8) и фиксирующие винты (5; 9) для регулируемого элемента и регулировочной пластины. Для повышения точности регулирования регулировочная пластина расположена с возможностью определения своей толщиной смещения регулируемого элемента, фиксирующий винт размещен в направляющем пазу, выполненном в регулировочной пластине. При этом регулировочный винт выполнен с буртиками и установлен в паз, выполненный в регулировочной пластине, а регулируемый элемент установлен с возможностью смещения относительно фиксирующего его винта [2].

2 Одномерная оптимизация

Дана функция: R(x)=1,5sin (x-1)

Найти максимум на интервале: [-2,2].

Строим график данной функции (рисунок 2).

Рисунок 2 – график функции R(x)=1,5sin (x-1).

По форме графика определяем что он имеет 1 экстремум, применяем метод деления отрезка пополам. Bспользуем систему Mathcad для решения данной задачи [3, c. 22]. Ошибка задается по х:  =0,05.

Находим середину отрезка (точка 0), в каждой из полови­нок (в левой и правой) находим значения функции с учетом погрешности  и, срав­ниваем их. Определяем, в какой из половинок находится экстремум (уравнение (1) и (2)).

x₁:=0,05

1.5·sin·(x₁-1)= - 1.22

R(x₁) = -1.22 (1)

x₂:= -0,05

1.5·sin·(x₂ – 1) = -1.301

R(x₂) = -1.301 (2)

В правой части находится экстремум, так как значение функции больше чем в левой.

В качестве следующего отрезка выбираем отрезок [0, 2]. Находим середину отрезка (точка 1), в каждой из полови­нок (в левой и правой) находим значения функции с учетом погрешности  и, срав­ниваем их. В зависимости от сравнения зна­чений функции в точках выбирают новый отрезок, решение производится аналогично решению в уравнениях (1) и (2).

x₃:= 1.05

1.5·sin·(x₃ – 1) = 0.075

R(x₃) = 0.075

x₄:= 0.95

1.5·sin·(x₄ – 1) = - 0.075

R(x₄) = - 0.075

Далее следуем аналогично. Выполняем еще 3 шага.

x₅:= 1.55

1.5·sin·(x₅-1) = 0.784

R(x₅) = 0.784

x₆:= 1.45

1.5·sin·(x₆ – 1) = 0.652

R(x₆) = 0.652

x₇:= 1.8

1.5·sin·(x₇ – 1) = 1.076

R(x₇):= 1.076

x₈:=1.7

1.5·sin·(x₈ – 1) = 0.966

R(x₈) = 0.966

x₉:= 1.925

1.5·sin·(x₉ – 1) = 1.198

R(x₉) = 1.198

x₁₀:= 1.822

1.5·sin·(x₁₀ – 1) = 1.099

R(x₁₀) = 1.099

Максимум функции находится в точке х9: 1.198

3 Многомерная безусловная градиентная оптимизация.

3.1 Метод градиента.

Метод градиента в чистом виде формирует шаг по переменным как функцию от градиента R(x) в текущей точке поиска. [1, c. 63].

Дана функция R(x₁, x₂) = (x₁)² + 2·(x₂ – 1.3)²

Требуется найти минимум функции.

Начальная точка: x₁ = -0.5; x₂ = 0.

Параметры поиска: коэффициент шага h = 0,1, пробный g = 0,02, погрешность Е = 0,01.

Алгоритм метода: алгоритм 1 (хⁱ⁺¹ =хⁱ - hgrad R(xⁱ)) (3).

Алгоритм коррекции шага: без коррекции коэффициента пропорциональности шага (h = const).

Способ вычисления производной: вычисление gradR с парными пробами.

h:= 0.1; g:= 0.02; E:=0.01

R(x₁, x₂):= (x₁)² + 2·(x₂ – 1.3)²

В начальной точке вычисляем градиент функции:

x₁:= - 0.5 x₂:= 0

R(x₁ + g, x₂) = 3.61

R(x₁ – g, x₂) = 3.65

R(x₁, x₂ + g) = 3.527

R(x₁, x₂ – g) = 3.735

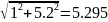
Значение критерия:

R(x₁, x₂) = 3.63

Делаем рабочий шаг №1 , получаем

x₁ = -0.4

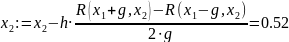
x₂ = 0.52

В новой точке опять вычисляем производные:

x₁:= - 0.4 x₂:= 0.52

R(x₁ + g, x₂) = 1.361

R(x₁ – g, x₂) = 1.393

R(x₁, x₂ + g) = 1.315

R(x₁, x₂ – g) = 1.44

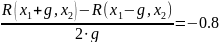
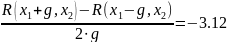
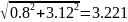
Значение критерия

R(x₁, x₂) = 1.377

Делаем рабочий шаг №2, получаем

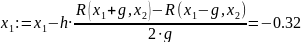
x₁ = -0.32

x₂ = 0.832

Далее вновь вычисляем производные и продолжаем расчет путем повторения шагов. В общем выполняем n кол-во шагов для нахождения оптимального значения.

x₁:= - 0.32 x₂:= 0.832

R(x₁ + g, x₂) = 0.528

R(x₁ – g, x₂) = 0.554

R(x₁, x₂ + g) = 0.504

R(x₁, x₂ – g) = 0.579

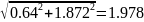
Рабочий шаг № 3

x₁ = -0.256

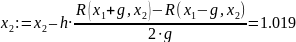
x₂ = 1.019

Вычисление производных

x₁:= - 0.256 x₂:= 1.019

R(x₁ + g, x₂) = 0.213

R(x₁ – g, x₂) = 0.234

R(x₁, x₂ + g) = 0.202

R(x₁, x₂ – g) = 0.246

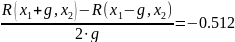
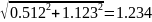
R(x₁,x₂)=0.223

Рабочий шаг №4

x₁ = -0.205

x₂ = 1.132

Вычисление производных

x₁:= - 0.205 x₂:= 1.132

R(x₁ + g, x₂) = 0.091

R(x₁ – g, x₂) = 0.107

R(x₁, x₂ + g) = 0.086

R(x₁, x₂ – g) = 0.113

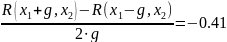
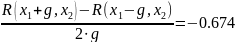
R(x₁,x₂)=0.099

Рабочий шаг № 5

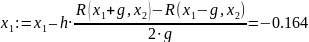
x₁ = -0.164

x₂ = 1.264

Вычисление производных

x₁:= - 0.164 x₂:= 1.264

R(x₁ + g, x₂) = 9.85·10³

R(x₁ – g, x₂) = 0.018

R(x₁, x₂ + g) = 0.012

R(x₁, x₂ – g) = 0.017

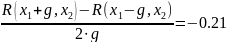
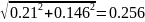
R(x₁,x₂)=0.014

Рабочий шаг № 6.

x₁ = -0.084

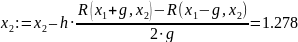
x₂ = 1.278

Вычисление производных

x₁:= - 0.084 x₂:= 1.278

R(x₁ + g, x₂) = 5.035·10^-3

R(x₁ – g, x₂) = 0.012

R(x₁, x₂ + g) = 7.044·10^-3

R(x₁, x₂ – g) = 0.011

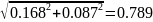
R(x₁,x₂)=7.99 ·10^-3

Рабочий шаг № 7.

x₁ = -0.067

x₂ = 1.278

Вычисление производных

x₁:= - 0.067 x₂:= 1.278

R(x₁ + g, x₂) = 2.563·10^-3

R(x₁ – g, x₂) = 7.931·10^-3

R(x₁, x₂ + g) = 4.599·10^-3

R(x₁, x₂ – g) = 6.695·10^-3

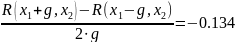
R(x₁,x₂)=4.847 ·10^-3

Рабочий шаг №8

x₁ = -0.054

x₂ = 1.292

Вычисление производных

x₁:= - 0.054 x₂:= 1.292

R(x₁ + g, x₂) = 1.258·10^-3

R(x₁ – g, x₂) = 5.553·10^-3

R(x₁, x₂ + g) = 3.177·10^-3

R(x₁, x₂ – g) = 4.435·10^-3

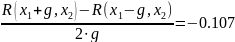
R(x₁,x₂)=3.006 ·10^-3

Рабочий шаг № 9

x₁ = -0.043

x₂ = 1.295

Вычисление производных

x₁:= - 0.043 x₂:= 1.295

R(x₁ + g, x₂) = 5.712·10^-4

R(x₁ – g, x₂) = 4.007·10^-3

R(x₁, x₂ + g) = 2.312·10^-3

R(x₁, x₂ – g) = 3.066·10^-3

R(x₁,x₂)=1.889 ·10^-3

Рабочий шаг № 10

x₁ = -0.034

x₂ = 1.297

Вычисление производных

x₁:= - 0.034 x₂:= 1.297

R(x₁ + g, x₂) = 2.222·10^-4

R(x₁ – g, x₂) = 2.971·10^-3

R(x₁, x₂ + g) = 1.77·10^-3

R(x₁, x₂ – g) = 2.223·10^-3

R(x₁,x₂)=1.197 ·10^-3

Рабочий шаг № 11

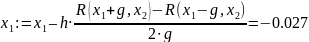
x₁ = -0.027

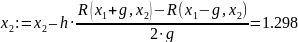
x₂ = 1.298

Вычисление производных

x₁:= - 0.027 x₂:= 1.298

R(x₁ + g, x₂) = 6.183·10^-5

R(x₁ – g, x₂) = 2.261·10^-3

R(x₁, x₂ + g) = 1.426·10^-3

R(x₁, x₂ – g) = 1.697·10^-3

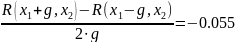
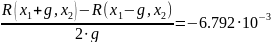
R(x₁,x₂)=7.613 ·10^-4

Рабочий шаг № 12

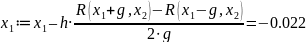
x₁ = -0.022

x₂ = 1.299

Вычисление производных

x₁:= - 0.022 x₂:= 1.299

R(x₁ + g, x₂) = 6.037·10^-6

R(x₁ – g, x₂) = 1.765·10^-3

R(x₁, x₂ + g) = 1.204·10^-3

R(x₁, x₂ – g) = 1.367·10^-3

R(x₁,x₂)=4.856 ·10^-4

После 12 шагов сводим значения расчетов в таблицу 1 и проверяем.

Таблица 1 – результаты расчетов после 12 шагов.

n	x1	х2	dR/dx1	dR/dx2	|gradR|	R
1	-0.5	0	-1	-5.2	5.295	3.63
2	-0.4	0.52	-0.8	-3.12	3.221	1.377
3	-0.32	0.832	-0.64	-1.872	1.978	0.54
4	-0.256	1.019	-0.512	-1.123	1.234	0.223
5	-0.205	1.132	-0.41	-0.674	0.789	0.099
6	-0.164	1.199	-0.328	-0.404	0.52	0.047
7	-0.131	1.239	-0.262	-0.243	0.357	0.025
8	-0.105	1.264	-0.21	-0.146	0.256	0.014
9	-0.084	1.278	-0.168	-0.087	0.189	0.00799
10	-0.067	1.287	-0.134	-0.052	0.144	0.004847
11	-0.054	1.292	-0.107	-0.031	0.111	0.003006
12	-0.043	1.295	-0.086	-0.019	0.088	0.001889
13	-0.034	1.297	-0.069	-0.011	0.07	0.001197
14	-0.027	1.298	-0.055	-0.00679	0.055	0.0007613
15	-0.022	1.299	-0.044	-0.004075	0.044	0.0004856

В последней точке модуль градиента практически равен заданной по­грешности (0,044 ≈ 0,01), поэтому поиск прекращается.

Строим график градиента (рисунок 3)

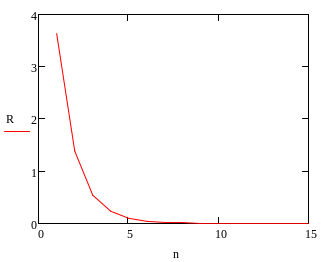
Рисунок 3 – построение графика