3.Закон распределения случайной величины
Цель Построить полигон распределения результатов замера , определить размах выборки, принять цену погрешности прибора (будем считать за 1 мкм )определить заданые интервалы ,расставить значения в заданные интервалы определить частность.
Определим размах выборки
R = Xmax - Xmin , R=230мкм (6.3) стр 21
R-размах выборки. Xmax – максимальное значение выборки. Xmin-минимальное значение выборки.
,
-размах выборки с учетом погрешности
прибора
-погрешность
прибора
R-размах выборки с учетом Ц.Д.П.
Определение заданных интервалов вычисляем по двум формулам, для определения нижней границы интервала используем формулу:
∆R
= 
мкм
(6.5)стр
22
Из этого следует распределение значений контролируемого параметра по интервалам, приведенное в таблице 3.
Для нахождения первого значения интервала воспользуемся формулой:
(6.8) стр 23
нижний
предел 1 интервала
верхний
предел 1
интервала
верхний
предел 2 интервала
Получаем первый интервал 19.5÷66.2.мкм. Для получения следующих интервалов прибавляем к предыдущему.
Таблица 3
Попадания значений измерений в заданные интервалы
-
Интервалы. мкм.
Частота, m
m/n
19.5-66.2
12
0,46
66.2-112.4
5
0,19
112.4-158.2
5
0,19
158.2-204.8
2
0,07
204.8-251
2
0,07
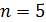
Сумма m=26
Сумма
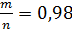
Рис. 2. Полигон распределения результатов замера
Вывод. По рис. 2 а также учитывая 9 степень точности и величину выборки n>20 (выборка маленькая ) принимаем закон нормального распределения (закон Гаусса).
4. Построение кривой нормального распределения
Цель Построить кривую нормального распределения ,расчитать значение точек вершины и перегиба кривой.
,
где: е – основание натурального логарифма.
Кривая нормального распределения характеризуется следующими
свойствами: она симметрична относительно оси ординат, и ветви ее асимптотически приближаются к оси абсцисс. Ордината вершины кривой
(при Ri=Rср) определяется из выражения [7, стр.21]:
=
,
(6.5) стр 21
где: ymax – значение максимума кривой нормального распределения.
2
На расстоянии ±σ от вершины кривая имеет две точки перегиба
(точки А и В) с ординатами [7, стр.21]:
= 0,0037 (6.6) стр 21
На расстоянии ±2σ от вершины кривая имеет две
точки С и D с ординатами:
= 0,00082, (6.7) стр 22
На расстоянии ±3σ от вершины кривая имеет три точки перегиба,
точки E и F с ординатами:
= 0,00007, (6.8)стр 22