2. Определим среднеквадратическое отклонение:

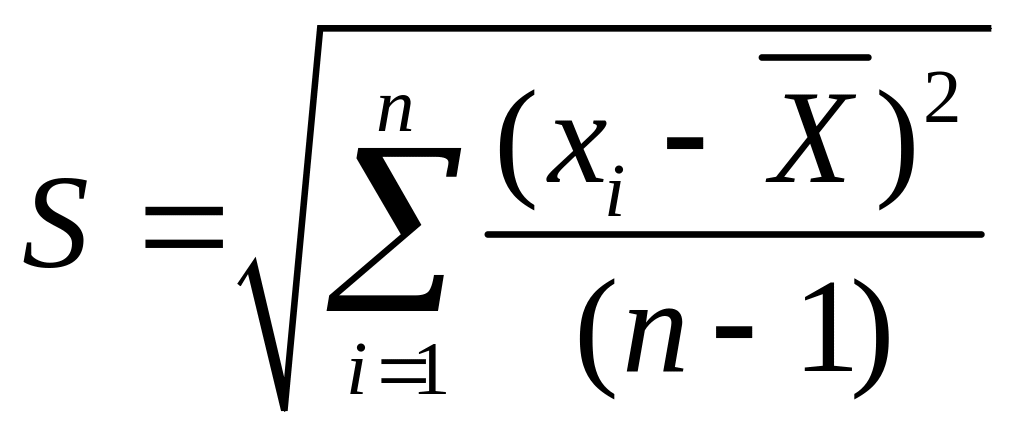
При n ≥ 26, принимаем (n-1)=n. Следовательно

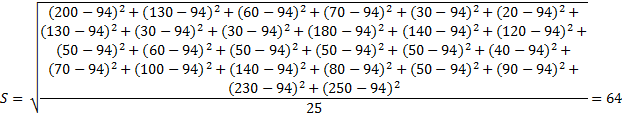
Определим допуск на отклонение Frr – радиального биения зубчатого венца, руководствуясь ГОСТ 1643 – 81. Для этого сначала определим диаметр делительной окружности зубчатого колеса по формуле:

230 мкм

Принимаем значение из таблицы 5 по ГОСТ 1643 – 81, а значит

Т = 100 мм

Разность между наибольшим и наименьшим действительными раз- деталей в партии называют размахом распределения или полем рассеивания: R = Rmax¬Rmin (6.3) стр 21

R=250-20=230мкм

Положение основных характеристик распределения случайной величины.

Рис 1

Вывод в данном разделе мы определили среднеарифмитическое значение Х,

определили среднеквадратическое отклонение S,расчитали диаметр делительной окружности зубчатого колеса ,определили допуск на отклонение радиального биения зубчатого венца ,построили график положения основных характеристик распределения случайной величины.Определили размах R.

2. Оценка грубых погрешностей измерений обработки

Цель. Грубые погрешности измерения и обработки нередко оказывают решающее влияние на оценку точности технологических процессов и приводят к тому, что отдельные результаты наблюдений по своей величине значительно отличаются от других. Если технолог убеждён, что такие наблюдения – результат ошибки, то эти наблюдения не следует учитывать при последующем анализе. Если же такой уверенности нет, то для определения того, является ли резко выделяющиеся измерения результатом грубой ошибки или случайного отклонения, необходимо использовать один из методов обнаружения грубых погрешностей эксперимента. Для оценки применим метод Гребса, который заключается в следующем. Предварительно по опытным данным выборки вычислим характеристики распределения. Среднее арифметическое значение Х и среднеквадратичное отклонение S. Затем определим величину квантиля по формуле:

(5.1) стр 18

где

- среднее квадратическое отклонение, мкм;

-резко выделяющееся (наибольшее или наименьшее) значение, мкм;

- среднее арифметическое случайной погрешности, мкм.

Задавшись процентом риска р, при котором грубая ошибка может быть принята за случайную (при технологических исследованиях чаще всего р=5%), по таблице 2 в зависимости от объёма выборки n находим критическое значение , которое сравниваем с ранее вычисленным значением по выше приведённой формуле.