
I. ПРЕДЕЛЫ
Какой предел называется первым замечательным пределом?
Какой предел называется вторым замечательным пределом?
Найти

Найдите предел

 .
.Найдите предел
 .
.Найдите предел
 .
.Чему равен
 ?
?Найдите предел

Найдите предел

Найдите предел

Найдите предел

Найдите предел

Найдите предел

Найдите предел

Найдите предел

II. НЕПРЕРЫВНОСТЬ И РАЗРЫВЫ
Указать точку разрыва, установить их характер

Указать точку разрыва, установить их характер

Указать точки разрыва, установить их характер

III. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ
Найти
 из уравнения arctg
y=x+y:
из уравнения arctg
y=x+y:Вычислить
 ,
если
,
если
 ,
,
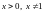
Вычислить
 ,
если
,
если

Найти производную функции
 ,
заданной неявно
,
заданной неявно

Вычислить , если

Найти производную функции , заданной неявно

IV. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
Найти координату x точки перегиба функции
 .
.Определить точку перегиба функции
 .
.Найти горизонтальную асимптоту функции
 .
.Написать уравнение касательной к кривой
 в точке с абсциссой
в точке с абсциссой
 .
.Найти наклонную асимптоту функции
 .
.Найти вертикальную асимптоту функции
 .
.Найти промежутки возрастания функции у =
 .
.
V. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Вычислить интеграл
 .
.Вычислить интеграл
 .
.Найти интегралы
 .
.Вычислить интеграл
 .
.Найти интеграл
 .
.Вычислить интеграл

Вычислить интеграл
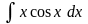 .
.Вычислить интеграл
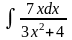 .
.Вычислить интеграл
 .
.Вычислить интеграл
 .
.
Вычислить интеграл
 :
:Вычислить интеграл
 :
:Вычислить интеграл
 :
:
Экзаменационные вопросы
Числовая последовательность. Монотонная, ограниченная, сходящаяся. Бесконечно большая. Бесконечно малая.
Свойства сходящихся последовательностей. Свойства бесконечно малых последовательностей. Связь между бесконечно большими и бесконечно малыми величинами.
Теорема Вейерштрасса о существовании предела.
Функция и методы ее задания. Классификация функций.
Односторонние пределы. Замечательные пределы.
Непрерывность функции в точке и на отрезке. Точки разрыва и их классификация.
Производная и дифференциал функции. Производная основных элементарных функции. Геометрический и физический смысл производной. Уравнение касательной и нормали.
Дифференцируемость функции. Основные правила дифференцирования. Производная сложной, обратной, неявной функции.
Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа, Коши).
Исследование функции. Определение локальных и глобальных экстремумов функции.
Необходимое и достаточное условия существования локальных экстремумов.
Направление выпуклости графика функции. Точки перегиба и асимптоты. Необходимое и достаточное условие существования точки перегиба графика функции.
Первообразная и неопределенный интеграл, его основные свойства.
Таблица основных интегралов и основные методы интегрирования.
Определенный интеграл и его свойства.
Оценки определенного интеграла. Теоремы о среднем.
Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.
Геометрические приложения определенного интеграла (вычисление площадей плоских фигур, длин плоских дуг, объемов тел вращения, площадей поверхностей вращения).
Понятие функции
 переменных.
Касательная плоскость и нормаль к
поверхности.
переменных.
Касательная плоскость и нормаль к
поверхности.Дифференцируемость сложной функции. Дифференциал.
Частные производные высших порядков; теорема о равенстве смешанных производных.
Понятие локального минимума (максимума), строгого локального минимума (максимума).
Необходимое условие локального экстремума; стационарные точки функции.
Достаточное условие локального экстремума; случай функции двух переменных.
Определение и свойства двойного интеграла. Сведение двойного интеграла к повторному.
Физические приложения двойного интеграла: вычисление массы пластины; статические моменты и моменты инерции материальной пластины относительно координатных осей; координаты центра тяжести материальной пластины.
Двойной интеграл в полярных координатах.
Числовые ряды. Сходящийся ряд, сумма ряда, необходимый признак сходимости ряда.
Достаточные признаки сходимости знакоположительного ряда.
Знакочередующийся ряд, его сумма и признак Лейбница.
Абсолютно и условно сходящиеся ряды.
Функциональный ряд, область сходимости функционального ряда.
Степенной ряд и теорема Абеля.
Радиус сходимости степенных рядов.
Ряд Тейлора. Условие разложимости функции в ряд Тейлора
Разложение в ряд Маклорена простейших функций.
Вычислить предел
 :
А)
e2
; В)
e;
С)2;
Д)
e1/2;
Е)1.
:
А)
e2
; В)
e;
С)2;
Д)
e1/2;
Е)1.Вычислить предел
 :
А)
:
А)
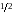 ;
В)3;
С)
;
В)3;
С) ;
Д)
;
Д) ;
Е)1.
;
Е)1.Найти предел функции
 :
А)1/4; В)1/2;
С)0; Д)1; Е)4
:
А)1/4; В)1/2;
С)0; Д)1; Е)4Найти предел функции
 :
А) 25/2; В)5/2; С)5; Д)2; Е)7
:
А) 25/2; В)5/2; С)5; Д)2; Е)7Найти предел функции
 :
А)2; В)4; С)3; Д)1; Е)5/2
:
А)2; В)4; С)3; Д)1; Е)5/2Найти предел
 :
А) -0.6; В)4; С)6; Д)-1; Е)0.6;
:
А) -0.6; В)4; С)6; Д)-1; Е)0.6;
Найти предел
 :
А)
:
А) ;
В)2; С)3; Д)1;
Е)
;
В)2; С)3; Д)1;
Е)
Найти предел
 :
А)
:
А) ;
В)
;
В) ;
С)0; Д)1; Е)
;
С)0; Д)1; Е)
Найти предел
 :
А)
:
А) ;
В)
;
В) ;
С)1; Д)0; Е)
;
С)1; Д)0; Е)
Найти предел
 :
А)-1;
В)0; С)2; Д)
;
Е)1
:
А)-1;
В)0; С)2; Д)
;
Е)1
Найти точки разрыва функции
 А)
А) ;
В)
;
В)
 ,
, ;
;
С)
 ,
,
 ;
Д)
;
Д) ;
Е) функция непрерывна
;
Е) функция непрерывна
Найти точки разрыва функции

А) ,
,
 ;
В)
,
;
С) функция непрерывна; Д)
,
;
;
В)
,
;
С) функция непрерывна; Д)
,
;
Е)
 ,
,
Найти точки разрыва функции

А)
функция непрерывна; В)
;
С) ;
Д)
;
Е)
,
;
Д)
;
Е)
,
Найти точки разрыва функции
А)
;
В)
;
С)
 ;
Д)
;
Д)
 ;
Е)
;
Е)
Указать точку разрыва, установить их характер

А) точка разрыва 1 рода; В) точка разрыва 1 рода; С) точка разрыва 2 рода;
Д) устранимая точка разрыва; Е) непрерывная функция
Указать точку разрыва, установить их характер
А) точка разрыва 1 рода; В) точка разрыва 1 рода; С) точка разрыва 2 рода;
Д) устранимая точка разрыва; Е) непрерывная функция
Указать точку разрыва, установить их характер

А) точка разрыва 1 рода; В) точка разрыва 1 рода; С) точка разрыва 2 рода;
Д) устранимая точка разрыва; Е) непрерывная функция
Вычислить
 ,
если
,
если

А)-1; В)0; С)1; Д)2; Е)-2
Вычислить производную функции
 :
:
А) ;
В)
;
В) ;
С)
;
С) ;
Д)
;
Д) ;
Е)
;
Е)
Найти производную функции
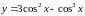 :
:
А) ;
В)
;
В)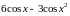 ;
С)
;
С) ;
;
Д) ;
Е)
;
Е)
Найти скорость равномерно ускоренного движения
 м/сек)
в момент времени t=2
сек.
м/сек)
в момент времени t=2
сек.
А)19,6; В)9,8; С) 98; Д)3; Е)0
Найти значения тангенса угла наклона касательной к кривой
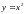 в точке
в точке

А)-2; В)0; С)1; Д)2; Е)-1
