V розділ
1.Розрахувати показники вибіркової сукупності та порівняти їх з показниками генеральної сукупності
Обчислимо показники генеральної і вибіркової сукупності на такому прикладі. Допустимо, що орендний колектив доглядає 100 корів. Для визначення середньої жирності молока, а також частки корів із жирністю 3,7 % і більше, спочатку візьмемо вибіркові проби від 30 корів, а потім - від 100 корів. Жирність молока буде такою, відсотків:
від 30 корів – 3,7; 4,0; 3,9; 3,5; 3,3; 3,8; 3,7; 3,8; 3,5; 3,4; 3,8; 3,7; 3,8; 3,5; 3,6; 3,4; 4,0; 3,9; 3,5; 3,3; 3,5; 3,3; 3,9; 3,4; 4,0; 3,6; 3,5; 3,8; 3,7; 3,8.
від 100 корів – 3,4; 3,8; 3,3; 3,6; 3,5; 3,7; 3,8; 3,7; 3,5; 3,4; 3,5; 3,7; 4,0; 3,9; 3,5; 3,8; 3,7; 3,3; 3,6; 3,7; 3,4; 3,8; 3,5; 3,3; 3,8; 3,6; 3,7; 3,5; 3,9; 3,5; 3,7; 3,5; 4,0; 3,9; 3,5; 3,8; 3,6; 3,7; 3,3; 3,7; 3,5; 3,8; 3,4; 3,7; 3,7; 3,5 3,6; 3,3; 3,4; 3,8; 3,8; 3,5; 3,4; 3,3; 3,8; 3,6; 3,7; 3,5; 3,5; 3,9; 3,5; 3,8; 3,4; 3,3; 3,8; 3,6; 3,5; 3,7; 3,9; 3,5; 3,7; 3,5; 3,9; 4,0; 3,8; 3,5; 3,7; 3,3; 3,6; 3,7; 3,4; 3,7; 3,7; 3,5; 3,8; 3,7; 3,5; 3,6; 3,8; 3,3; 3,4; 3,2; 3,6; 4,0; 4,1; 3,6; 3,3; 3,9; 3,6; 3,7; 3,0.
За наведеними даними визначимо показники вибіркової сукупності:
середня
жирність молока
;
дисперсія
жирності молока
=
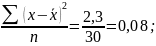
частість
корів із жирністю молока 3,7 % і більше
Показники генеральної сукупності становитимуть:
середня
жирність молока
;
дисперсія
жирності молока
частка
корів із жирністю молока 3,7 % і більше
=0,46
Отже, вибіркова середня дорівнює 3,65 %, вибіркова дисперсія – 0,08, а частість – 0,5; відповідно генеральна середня – 3,60 %, генеральна дисперсія – 0,044, а частка – 0,46. В абсолютному виразі різниця між середніми дорівнює 0,05 %, а між частістю і часткою-0,04. Різниця між показниками вибіркової і генеральної сукупностей становить помилку репрезентативності.
2.Розрахувати середню живу масу ремонтних телиць, за безповоротної вибірки та граничну помилку.
Розглянемо на прикладі: У спеціалізованому господарстві з вирощування нетелей для визначення приросту живої маси ремонтних телиць у віці від 12 до 15 місяців проведено контрольне зважування. З групи 512 корів взято 62 голови. Результати наведено в таблиці 5.1.
Таблиця 5.1.
Розподіл ремонтних телиць контрольної групи за живою масою
Жива маса телиць, кг |
Кількість телиць |
270-280 |
15 |
280-290 |
11 |
290-300 |
19 |
300-310 |
10 |
310-320 |
4 |
З імовірністю р=0,95 потрібно визначити живу масу телиць у генеральній сукупності і частку телиць живою масою 300 кг і більше.
Спочатку визначимо середню живу масу телиць у вибірковій сукупності:
=
Вибіркова дисперсія живої маси телиць
=
Скоригуємо
вибіркову дисперсію на множник
;
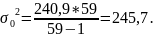
За таблицею «Значення інтеграла імовірності» встановимо, що за рівня імовірності 0,95 нормоване відхилення t=1,96.
Отже,
N=509;
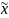=298,9;
=245,7;
t=1,96;
n=59.
Підставивши ці дані у формулу граничної помилки вибірки у разі без повторної вибірки, матимемо:
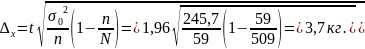
Оскільки помилка вибірки може мати додатний або від’ємний знак, то можливі межі середньої величини у генеральній сукупності визначають з формулою:
299-3,7
299+3,7
295,3 302,7
Отже, з імовірністю 0,95 можна гарантувати, що різниця між вибірковою середньою і генеральною середньою не перевищить 3,7 кг, а середня жива маса всіх телиць знаходиться в межах від 295,3 до 302,7 кг.
Частка телиць із живою масою 300 кг і більше у вибірковій сукупності становитиме
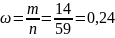
Скоригована дисперсія альтернативної ознаки
Гранична помилка частки телиць із живою масою 300 кг і більше:
Можливі межі частки у генеральній сукупності обчислюють за формулою
24,0-10 24,0+10
14 25;
Отже, з імовірністю 0,95 можна гарантувати, що різниця між частістю і часткою не перевищить 0,1, а частка телиць із живою масою 300 кг і більше у генеральній сукупності знаходиться в межах від 14 до 25 %.