Глава 2. Линейные уравнения второго порядка

§6. Классификация линейных уравнений второго порядка

Будем рассматривать уравнения с частными производными второго порядка, линейные относительно старших производных, т.е. имеющие вид

(6.1)

где являются функциями и .

С помощью преобразования переменных

допускающего обратное преобразование (для этого достаточно потребовать, чтобы функциональный определитель

был отличен от нуля), можно получить уравнение, эквивалентное исходному. Нас будет интересовать вопрос: как выбрать новые переменные и , чтобы относительно них уравнение имело наиболее простой (канонический) вид.

Попытаемся выбрать переменную так, чтобы коэффициент в уравнении (6.4) был равен нулю. Для этого необходимо, чтобы было решением уравнения

(6.6)

Уравнение (6.6) можно записать в виде произведения

Таким образом, решение уравнения (6.6) свелось к решению двух линейных однородных уравнений первого порядка

(6.7)

Из §3 следует, что для решения уравнений (6.7) надо найти общий интеграл каждого из уравнений

(6.8)

На вид решений уравнений (6.8) существенно влияет знак подкоренного выражения . По знаку этого выражения определяется тип уравнения (6.1).

Будем называть уравнение (6.1) в точке

гиперболического типа, если ,

эллиптического типа, если ,

параболического типа, если .

Можно убедиться в справедливости равенства

из которого следует, что тип уравнения не меняется при преобразовании переменных.

Следует отметить также, что тип уравнения зависит от точки и в разных точках может быть разным.

Пример 6.1. Рассмотрим уравнение

(6.9)

здесь и , следовательно,

Тем самым при уравнение (6.9) гиперболического типа, при – параболического типа, а при – эллиптического типа.

§7. Приведение линейных уравнений второго порядка

к канонической форме

Уравнение

(7.1)

будем называть характеристическим для уравнения (6.1), а его интегралы – характеристиками. Уравнение (7.1) распадается на два уравнения (6.8) и играет основную роль в задаче приведения к каноническому виду уравнения (6.1). Затем, что для уравнения гиперболического типа характеристики действительные и различные, для уравнений эллиптического типа – комплексные и различные, а для уравнений параболического типа обе характеристики действительные и совпадают.

Рассмотрим дифференциальное уравнение второго порядка с постоянными коэффициентами вида:

где a, b, c – постоянные коэффициенты.

Для определения задаются либо начальные условия , (задача Коши), либо краевые , (двухточечная краевая задача).

Общее решение неоднородного уравнения имеет вид , где - общее решение неоднородного уравнения; - общее решение однородного уравнения; - частное решение неоднородного уравнения.

- общее решение однородного уравнения, определяется корнями характеристического уравнения . Рассмотрим возможные при этом случаи:

1 случай: корни уравнения действительные и разные. В этом случае - .

2 случай: корни уравнения действительные и равные . В этом случае - .

3 случай: корни уравнения комплексно сопряженные: , где - действительные числа, i – мнимая единица ( ). В этом случае - .

Вид - частного решения неоднородного уравнения, зависит от правой части уравнения и представляется в аналитической форме лишь для определенных частных случаев . Рассмотрим возможные при этом случаи:

1 случай: если - многочлен степени m. В этом случае также находим в виде многочлена m-й степени: . Коэффициенты - подлежат определению. Для этого в левую часть уравнения - подставляют соответственно: вместо - выражение , вместо - и вместо - , а соответственно в правую часть – выражение . Приравнивая коэффициенты при свободных членах и множителях , получим m+1 алгебраических уравнений для определения m+1 коэффициентов .

2 случай: если . В зависимости от корней характеристического уравнения возможны различные варианты расчета .

Вариант а) корни характеристического уравнения - не совпадают с величиной ( ). В этом случае частное решение неоднородного уравнения имеет вид , где .

Вариант б) корни характеристического уравнения - действительные и разные, а величина равна одному из них (или , или ). В этом случае частное решение неоднородного уравнения имеет вид , где .

Вариант в) корни характеристического уравнения - действительные и равны величине (то есть ). В этом случае частное решение неоднородного уравнения имеет вид , где .

3 случай: если . В зависимости от корней характеристического уравнения возможны различные варианты расчета .

Вариант а) корни характеристического уравнения - действительные или комплексно сопряженные , при этом либо , либо , то ищется в виде . Коэффициенты С и D подлежат определению, для чего в левую часть подставляют соответственно вместо - , вместо - и вместо - , а в правую часть – выражение . Приравнивая слева и справа коэффициенты при множителях получим систему линейных уравнений, из которых определяем значения коэффициентов С и D.

Вариант б) если корни характеристического уравнения - чисто мнимые , то ищется в виде . Коэффициенты С и D подлежат определению, для чего в левую часть подставляют соответственно вместо - , вместо - и вместо - , а в правую часть – выражение . Приравнивая слева и справа коэффициенты при множителях получим систему линейных уравнений, из которых определяем значения коэффициентов С и D.

Если - является линейной комбинацией рассмотренных выше функций, то каждому входящему в слагаемому будет отвечать своя часть , которая определяется одним из указанных способов

Пример:

Найти решение задачи Коши:

Решение:

Определим корни характеристического уравнения . Дискриминант равен , следовательно

То есть мы имеем 1 случай, когда корни действительные и разные. В этом случае .

Тогда найдем, скомбинировав два случая, когда и , отсюда .

Следовательно, первая производная равна , а вторая - . Чтобы определить коэффициенты А, В, С, E, F необходимо в левую часть уравнения подставим соответственно значения , и получим

Упростим выражение:

Сгруппируем данные при множителях

Приравнивая слева и справа коэффициенты при множителях получим систему линейных уравнений, из которых определяем значения коэффициентов А, В, С, E, F.

Следовательно

Общее решение неоднородного уравнения имеет вид , а ее первая производная . Определим коэффициенты С₁ и С₂ подставив начальные условия и соответственно в и в , отсюда получим:

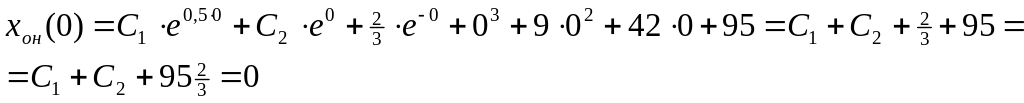
Решим систему

следовательно

Ответ: